一种紧支撑权函数性质的推导及空间插值实验

李　佳，段　平，盛业华，吕海洋，张思阳

(1.云南师范大学　旅游与地理科学学院，云南 昆明 650050；2.南京师范大学　虚拟地理环境教育部重点实验室，江苏 南京 210023；3.江苏省地理环境演化国家重点实验室培育建设点，江苏 南京 210023；4.江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023)



一种紧支撑权函数性质的推导及空间插值实验

李佳1,2,3,4，段平1,2,3,4，盛业华2,3,4，吕海洋2,3,4，张思阳2,3,4

(1.云南师范大学旅游与地理科学学院，云南 昆明 650050；2.南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210023；3.江苏省地理环境演化国家重点实验室培育建设点，江苏 南京 210023；4.江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023)

在空间插值方法中，权函数是影响空间插值精度的重要因素之一，通常需要选择具有性质较好的权函数进行空间插值。推导一种紧支撑权函数的性质，以铁矿品位为数据源，采用紧支撑权函数进行空间插值，最终验证该紧支撑权函数的优良性质：具有较高的插值精度。推导的紧支撑权函数性质可为后期构建新的紧支撑权函数作为一种借鉴。

紧支撑权函数；空间插值；反距离权重；铁矿品位

地理空间现象是连续变化的，通常为了表达连续的地理空间现象，需要建立连续的空间场。受观测成本、观测不可重复性等原因，只能在研究区域中采集到有限的散乱样本数据，空间插值方法就是利用这些有限的散乱样本数据建立一个连续函数模型，并计算地理空间任意位置上的特征属性，最终重建整个空间场的空间分析方法[1-2]。空间插值方法主要确定参考点的选择和权函数。当参考点确定后，权函数决定插值的精度。

国内外学者对空间插值方法中权函数进行大量的研究，如在经典的Shepard插值方法中权函数是以幂函数为倒数的函数[3]，Bekele，Ping，Lloyd分别选取幂函数的不同次数(1～5)进行插值实验[4-6]，Rühaak等人认为幂函数的次数应该根据观测点的可信度来动态变化，Lu 等人则认为幂函数次数应该根据参考点的密度自适应变化[7]，史利民从数学曲面的角度定义几类新的权函数[8]，徐遵义从权函数的衰减性上对Shepard插值方法中的权函数进行改进[9]，李正泉认为权函数的定义应该顾及插值参考点的方向遮蔽性，提出权函数应该考虑到反映方向的调和权重系数[10]。上述各种权函数的研究集中在构建新的权函数和对原始权函数改进，而对于权函数数学性质的研究较少，实际上权函数的数学性质指导着权函数的构建和改进。基于此，本文证明了一种常见的紧支撑权函数的性质，并采用该紧支撑权函数对模拟数据和实际的采样数据进行空间插值实验，实验表明本文采用的紧支撑权函数是一种插值精度较高的权函数，本文证明的紧支撑函数性质可为后期构建新的紧支撑函数作为一种指导。

1　空间插值方法中常见的权函数

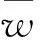
(1)

式中：wk表达式常见的有3种，均是与距离有关的函数：

(2)

式中：μ为幂函数的次数，可选候选值为1、2、3、4、5等，但一般取2。

(3)

(4)

其中

(5)

式中：Rw为设置的紧支撑半径。

从数学建模上分析，只要权函数的衰减性和光滑性越好，则插值效果越理想。而采用空间插值方法重建整个连续的空间场过程可以理解为数学建模过程。因此，在空间插值方法中，选择的权函数应该具备较好的衰减性和光滑性。上述各式中权函数是一个衰减性函数，随着距离的增加权函数对其插值点的贡献越小，一般的权函数都具备衰减性，而光滑性表现在权函数的偏导数相等，式(4)是一种具有较好的光滑性的紧支撑权函数，给出权函数光滑性的证明。

2　一种紧支撑权函数性质的证明

以二维情况为例，给出式(4)紧支撑权函数的基本性质，在此基础上给出偏导数相等的证明。

2.1紧支撑权函数的基本性质

当插值点(x, y)趋近于某个已知点(xj, yj)时，即(x,y)→(xj,yj)分为两种情况：

1)当j=k时，可以认为第k个点在wk处的wk的值为无穷大。

wk(xj,yj)→∞，而权重值为

(6)

分母：

w1+w2+…+wj+…+wk+…+

wn～wj(xj,yj)→∞.

(7)

(8)

(9)

(10)

2.2紧支撑权函数偏导数相等的证明

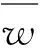
1)若(x,y)→(xj,yj)=(xk,yk)，则：

wk(xk,yk)→∞，wj(xk,yk)→有界量

(11)

(12)

其中

(13)

(14)

其中

(15)

(16)

(17)

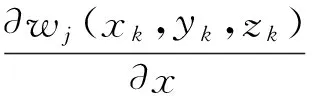
(18)

其中

(19)

(20)

(21)

(22)

2)若(x,y)→(xj,yj)≠(xk,yk)，

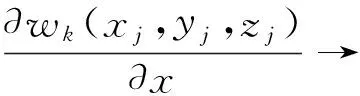
(23)

M1，M2与上述相同，均为有界量。则式(23)中各分量为

(24)

(25)

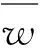
3　铁矿品位的空间插值实验与空间场重建

3.1铁矿品位的空间插值实验分析

为了验证本文推导的紧支撑权函数的性质，采用与紧支撑权函数同一类型的其它权函数进行反距离权重(Inverse Distance Weighted，IDW)空间插值实验对比，插值模型为

(26)

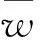
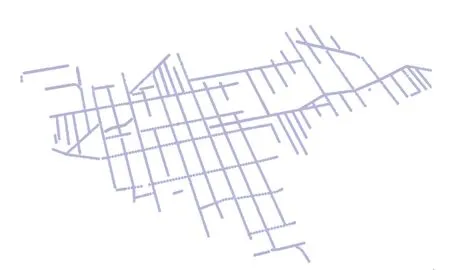
图1　矿体水平巷道钻孔数据空间分布

为了消除各种插值方法中参考点不同而影响插值误差分析，因此需要各种插值方法所采用的参考点数量相同，本文采用最邻近的30个点作为参考点，插值点与最邻近的第30个点的距离作为紧支撑权重的半径Rw。采用交叉验证统计各种插值方法的最小误差(Min)、最大误差(Max)、平均误差(ME)、均方根误差(RMSE)，如表1所示。

表1中紧支撑权函数的Min较大，但实际数值也趋近于0，认为紧支撑权函数在Min方面与另外几种插值方法无差异，而在Max方面，紧支撑权函数插值与式(2)权函数插值误差近似，但是这二种权函数插值都不如式(3)权函数插值的误差大，说明紧支撑权函数可能出现某个局部点的误差较大。就ME和RMSE而言，紧支撑权函数插值方法的这二项误差指标最小，而这二种误差指标是评价插值方法总体性能的最重要指标[13]，说明紧支撑权函数插值的总体误差最小，精度最高。从插值类型分析，与紧支撑权函数相似的几种权函数插值误差精度均优于克里金插值和薄板样条插值，4种误差最大的是克里金插值，其次是薄板样条插值，其原因是这二种插值方法所涉及的插值模型参数需要一定的人工经验，如果设置的不合理可能引起较大误差。

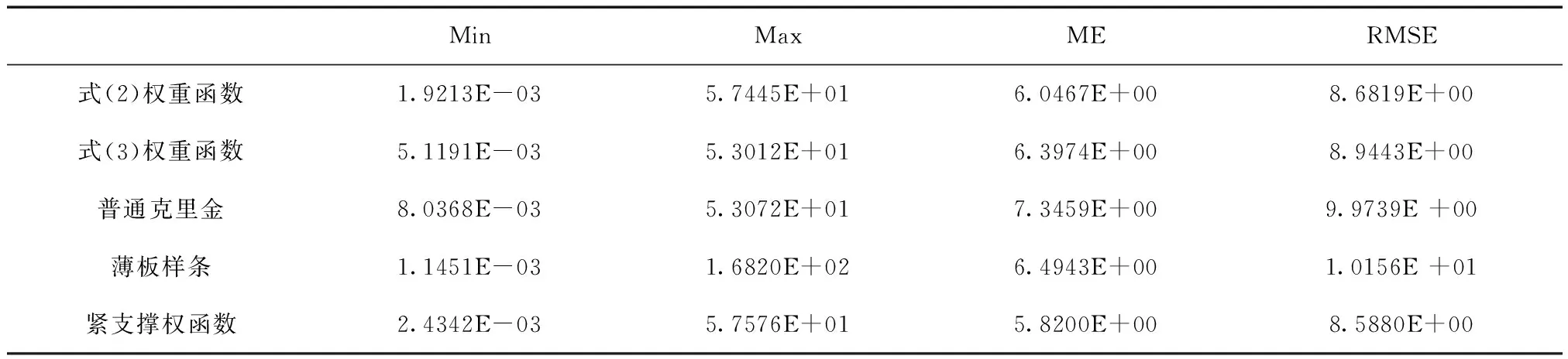
表1　各种插值方法误差统计指标

3.2铁矿品位的空间场重建

分别采用5种插值方法对铁矿品位进行空间场重建，如图2所示中(a)、(b)、(c)、(d)、(e)分别为采用式(2)权函数的IDW插值、式(3)权函数的IDW插值、紧支撑权函数插值、薄板样条插值、克里金插值的铁矿品位空间场重建结果，各插值结果的边界出现锯齿状，其原因是裁剪的多边形有锯齿状，但不影响空间场重建的分析。

从图2中可知，采用同一类型权函数插值方法(式(2)和式(3)权函数及紧支撑权函数)建立的空间场整体形态近似，但是采用式(2)和式(3)权函数空间插值方法的空间场呈现出整体“模糊”，而紧支撑权函数构建的空间场呈现出的光滑性和连续性是优于其他二种权函数插值方法，这也与3.1节中分析的插值误差结论相对应，插值方法误差越小表现在构建的空间场越光滑和越连续。与其他不同类型的样条函数插值和克里金插值比较，从空间场形态上分析，样条函数插值方法与其他方法的形态相差较大，主要原因与在3.1节中的各项误差最大相应，但是其空间场表明的光滑性和连续性较好，但是从光滑性和连续性不能判定插值方法的好坏，要与精度一起综合评价插值方法，而采用克里金插值方法重建的空间场形态与紧支撑权函数及其他权函数的空间场形态大体一样，其空间场整体上光滑性和连续性也较好，但是在3.1节中的误差不及紧支撑权函数空间插值。

综上所述，从插值方法的各种误差指标的总体性能及重建的空间场形态的连续性和光滑性分析，可知本文推导的紧支撑权函数在空间插值中表现较优。

图2　采用5种插值方法构建的铁矿品位空间场

4　结　论

紧支撑权函数的数学性质影响插值精度，本文推导一种紧支撑权函数的数学性质，通过实验验证采用该紧支撑权函数插值具有较高的插值精度，同时推导的紧支撑权函数性质可为后期构建新的权函数作为一种指导。

[1]段平,盛业华,李佳,等.自适应的IDW插值方法及其在气温场中的应用[J].地理研究,2014,33(8):1417-1426.

[2]张思阳,盛业华,段平,等.顾及各向异性的CSRBF空间插值及其在气温场重建中的应用[J].地理与地理信息科学,2014,30(7):117-121.

[3]RANKE R.Scattered data interpolation: tests of some methods[J].Mathematics of computation,1982,38(157): 181-200.

[4]BEKELE A,DOWNER R G,WOLCOTT M C,el al.Comparative evaluation of spatial prediction methods in a fieldexperiment for mapping soil potassium [J].Soil Science,2003,168(1):15-28.

[5]PING J L,GREEN C J,ZARTMAN R.Exploring spatial dependence of cotton yield using global and local autocorrelation statistics [J].Field Crops Research,2004,89(2): 219-236

[6]LLOYD C D.Assessing the effect of integrating elevation data intothe estimation of monthly precipitation in Great Britain[J].Journal ofHydrology,2005,308(1): 128-150.

[7]LU G Y,WONG D W.An adaptive inverse-distance weighting spatial interpolation technique[J].Computers & Geosciences,2008,34(9): 1044-1055.

[8]史利民,王仁宏.几种基于散乱数据拟合的局部插值方法[J].数学研究与评论,2006,26(2): 283-291.

[9]徐遵义,姜玉祥,赵亮,等.改进的Shepard算法及其在重力异常插值中的应用[J].武汉大学学报(信息科学版),2010,35(4):477-480.

[10] 李正泉,吴尧详.顾及方向遮蔽性的反距离权重插值法[J].测绘学报,2015,44(1): 91-98.

[11] 黄静,王爱倩,翟世龙.基于Kriging方法的负偏态分布数据的空间插值研究[J].测绘工程,2015,24(8):16-19

[12] 张子昕，周强波.空间插值算法在GIS中的应用[J].测绘与空间地理信息，2015,38(2)：103-107.

[13] 焦永清,李斌,张坤.基于空间可视化的气温插值方法比较[J].测绘工程,2013,22(5):62-64.

[责任编辑：李铭娜]

Theoretical derivation of compactly supported weight function andits application to spatial interpolation

LI Jia1,2,3,4,DUAN Ping1,2,3,4, SHENG Yehua2,3,4,LYU Haiyang2,3,4, ZHANG Siyang2,3,4

(1. College of Tourism and Geographical Sciences, Yunnan Normal University, Kunming 650500, China;2. Key Laboratory of Virtual Geographic Environment (Nanjing Normal University), Ministry of Education, Nanjing, 210023, China;3. State Key Laboratory Cultivation Base of Geographical Environment Evolution (Jiangsu Province), Nanjing, 210023, China;4. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China)

The weight function is one of the important factors that influence the spatial interpolation precision in many spatial interpolation methods. Weight function with better mathematical property is selected with spatial interpolation methods. Based on it, the mathematical property of compactly supported weight function is deduced in this paper. Iron ore grade sampling data as data source is used in compactly supported weight function interpolation experiment. By experimental validation, compactly supported weight function with fine properties has better precision and versatility. The mathematical property derivation of compactly supported weight function can be a guide for building a new compactly supported weight function.

compactly supported weight function; spatial interpolation; inverse distance weighted; iron ore grade

10.19349/j.cnki.issn1006-7949.2016.11.002

2016-01-23

国家自然科学基金资助项目(41271383)；云南师范大学博士基金资助项目(01300205020503128)

李佳(1984-)，女，讲师，博士.

P223

A

1006-7949(2016)11-0007-05