递进式预测模型在滑坡变形预测中的应用

谌　伟

(陕西铁路工程职业技术学院，陕西 渭南，714000)



递进式预测模型在滑坡变形预测中的应用

谌伟

(陕西铁路工程职业技术学院，陕西 渭南，714000)

为达到提高滑坡变形预测精度的目的，利用量子算法和粒子群算法对支持向量机进行优化，并利用马尔科夫链对滑坡变形预测误差进行修正，综合构建滑坡变形的递进式预测模型。结果表明：通过量子算法及粒子群算法对支持向量机优化，克服支持向量机参数选取困难，实现预测过程的全局优化，并经过MC误差修正模型对滑坡变形预测值误差修正，提高预测精度及预测值稳定性，验证预测模型可行性和有效性，为滑坡变形预测提供一种新的预测方法。

滑坡；支持向量机；粒子群算法；误差修正

滑坡是一种常见的自然地质灾害，滑坡的变形预测能有效地评价滑坡的稳定性，因此，对其变形研究具有重要的意义。在研究过程中，支持向量机被广泛的应用于滑坡研究中，如黄发明等[1]利用PSO—SVM预测模型，对滑坡所处的地下水位进行预测，有效的反映出滑坡区域地下水系统的演化特征；赵艳南等[2]则先利用粗糙集理论分析滑坡变形的核因子，并建立粒子群支持向量机预测模型，结果表明该模型的科学性和适用性；杨虎等[3]则进一步将小波分析与支持向量机结合，得出滑坡变形的混沌特性，较单一的支持向量机模型，可提高预测精度；张俊等[4]则将时间序列与PSO—SVR模型进行耦合，对滑坡的变形进行综合预测，取得较好的效果；谭龙等[5]则将逻辑回归与支持向量机进行结合，对滑坡的敏感性因素进行评价，为滑坡危险区的划分提供较好的依据。上述研究都为支持向量机在滑坡中的应用提供较好的实践依据，但各种预测模型具有其适用性，因此将量子算法引入支持向量机的优化过程中，仍需进行必要的研究，本文在预测过程中，构建的误差修正阶段，对降低预测误差，提高预测精度，具有重要的意义。

因此，本文将量子算法和粒子群算法同时引入支持向量机的优化过程中，探讨支持向量机的全局优化，并采用马尔科夫链对滑坡的预测误差进行修正，建立滑坡变形的递进式预测模型，以达到对滑坡变形预测的递进式预测研究，探讨该方法在滑坡变形预测中的应用可行性，验证其有效性和适用性。

1　基本原理

1.1支持向量机

支持向量机能实现输入信息在高维空间的投射，进而实现非线性问题在高维空间的线性处理。该理论采用机械学习方法，能很好解决非线性、小样本及高维数等问题，具有较好的全局优化能力，具有较高的预测精度。在支持向量机的预测过程中，估计函数可表示为

(1)

同时，不敏感损失函数可以实现对估计函数的转化，并将不敏感函数ε表示为

(2)

而在上述转化过程中，具有如下约束条件：

(3)

式中：ξi,ξi*为松弛因子;C为惩罚因子;b为偏置量。

另外，为达到全局优化的目的，应进行二次规划求解，并采用对偶理论进行转化，并将对偶式表示为

(4)

而在二次规划的过程中，具有如下约束条件：

(5)

最后可将支持向量机的预测模型表示为

(6)

1.2量子粒子群优化支持向量机[6]

量子粒子群优化支持向量机是采用粒子群法和量子法对支持向量机进行参数优化，进一步提高优化变量在搜索区域内的最优值。将两种优化过程的基本原理介绍如下：

1.2.2粒子群优化算法

粒子群优化算法是一种能够模仿鸟群觅食行为的优化算法，其基本思想是将优化问题或对象设定为N维空间中的一个点，将其称为“粒子”。在优化过程中，各粒子在每次迭代中的速度是由其目前的速度、位置的当前最优解进行调整和修正，进而实现对粒子位置的优化。粒子速度及位置的迭代可表示为

(7)

式中：i为第i个粒子;d为粒子维数;t为粒子第t代;w为惯性权重系数;c1为认知权重系数;c2为社会权重系数;r1,r2为[0,1]之间的随机数。

1.2.2量子优化算法

粒子群优化主要是通过改变粒子的速度和位置，不断搜寻最优点，但在该过程中，粒子的运动线路是在经典力学状态下进行的，因此粒子群优化的区域具有一定的缺陷，缺少全局的优化。为实现支持向量机在预测过程中的全局最优，本文将量子优化算法和粒子群优化算法进行结合，通过量子算法对粒子群算法的改进，实现粒子搜寻轨迹的不确定性，达到粒子在全局的最优解。

综上所述，本文采用量子粒子群优化算法对支持向量机进行优化求解，最大限度地实现需优化变量在全局内达到最优或接近最优。本文将适应值的函数定义为

(8)

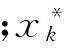
1.3MC误差修正模型

为达到进一步提高预测精度的目的，本文在优化支持向量机预测结果的基础上，再对预测误差进行修正，实现对滑坡变形的递进预测。

结合马尔科夫链的基本原理，将预测值的相对误差进行划分，共划分为n个区间，即S=[S1，S2，…，Sn]，并将由状态Si经过m步转变到Sj状态的概率表示为

(9)

式中：Mij(m)为状态转移所需的次数；Mi为Si状态的个数。

同时，将第m步时状态的转移矩阵表示为

(10)

利用位移转移矩阵，可以实现对预测值误差的修正，其过程是选取距预测时步最近的n个实测值，并根据转移矩阵中的第i个实测值经过m步转变到预测状态时步的概率，将n个概率进行求和，将最大值的误差状态和预测的相对误差时的状态看作为同一状态。

本文将预测相对误差的中点看作最大可能的预测相对误差，并将可能的预测值表示为

(11)

式中：F(x)为修正后预测值；f(x)为预测值；ΔU，ΔD为预测相对误差的上下限；Δ*为平均相对误差。

1.4预测步骤

本文结合上述各方法的基本原理，建立滑坡变形的递进式预测模型，其预测步骤为：

1)基于滑坡的变形数据，采用支持向量机对滑坡变形进行预测，作为滑坡变形预测的基础预测模型；

2)利用量子粒子群优化算法对支持向量机的预测进行优化，并对比优化前后的预测值，验证本文优化模型的适用性，完成对滑坡变形的一阶递进预测；

3)基于预测相对误差，构建出MC误差修正模型的转移矩阵，实现对滑坡变形预测值的进一步修正，完成对滑坡变形的二阶递进预测，得到本文滑坡变形的最终预测值。

2　实例分析

2.1工程概况

本文实例来源于文献[7]，滑坡区域所处的地质环境较为复杂，为一公路滑坡，由上到下的地层分布主要是填土、根植土、残坡积层及冲洪积层、枣市组泥质粉砂岩、砾岩等。同时，滑坡所处地区降雨较为充沛，岩层吸水易软化，易形成滑坡。在K1503+495～K1503+535区间的边坡在降雨作用下，出现变形，并有下滑的迹象。在滑坡上布设4个监测点，采用固定式测斜探头对滑坡的变形进行监测，通过对滑坡变形的现场监测，共监测24个监测周期，滑坡的变形情况如图1所示。

图1　滑坡累计变形曲线

2.2一阶递进预测分析

结合支持向量机模型及优化支持向量机模型的基本原理，对滑坡的4个监测点数据进行预测，并选取第19～24周期的数据作为验证样本，通过预测得出滑坡一阶递进模型的结果如表1所示。

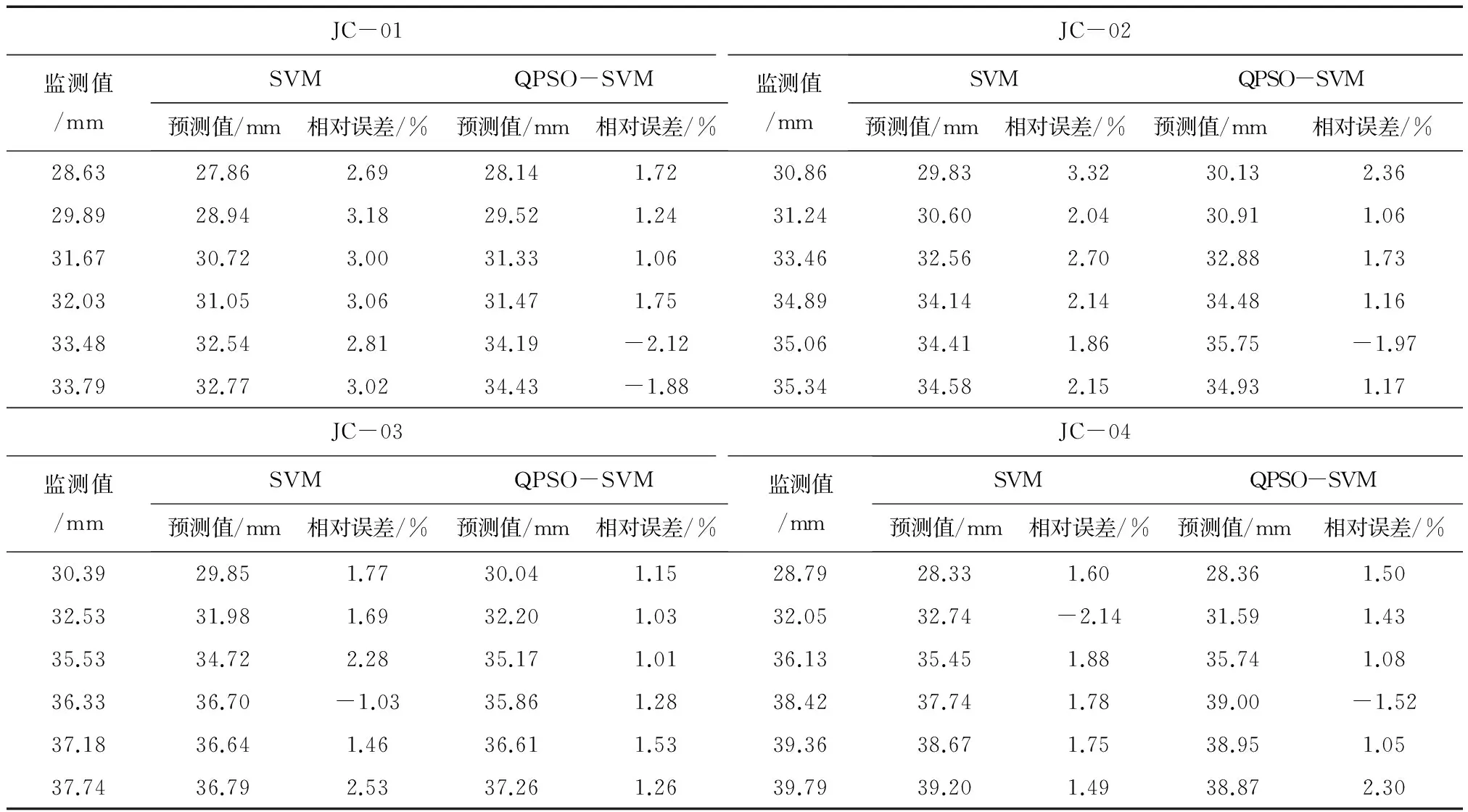
表1　滑坡一阶递进预测结果统计

对比各监测点在一阶递进前后的预测结果可知，通过对支持向量机预测模型的优化，均不同程度提高预测精度，支持向量机预测模型的预测相对误差多在2%～4%之间，而优化支持向量机预测模型的预测相对误差多在1%～2%之间，但相互之间也具有一定的差异，如不同监测点在不同预测模型及各监测周期的预测相对误差具有较大的不同和差异。在支持向量机预测模型中，各监测点在不同周期预测值中的最大相对误差为3.32%，最小相对误差为-2.14%，而在优化支持向量机的预测模型中，各监测点在不同周期预测值中的最大相对误差为2.36%，最小相对误差为-2.11%。

综上所述，各预测模型的预测结果具有一定的差异，且通过模型优化，提高预测精度，验证本文一阶递进预测模型具有其有效性，也证明递进预测的必要性。

2.3二阶递进预测分析

基于一阶递进预测的结果，结合二阶递进预测的MC误差修正模型，对滑坡的变形进行进一步的误差修正，二阶递进预测模型的结果如表2所示。

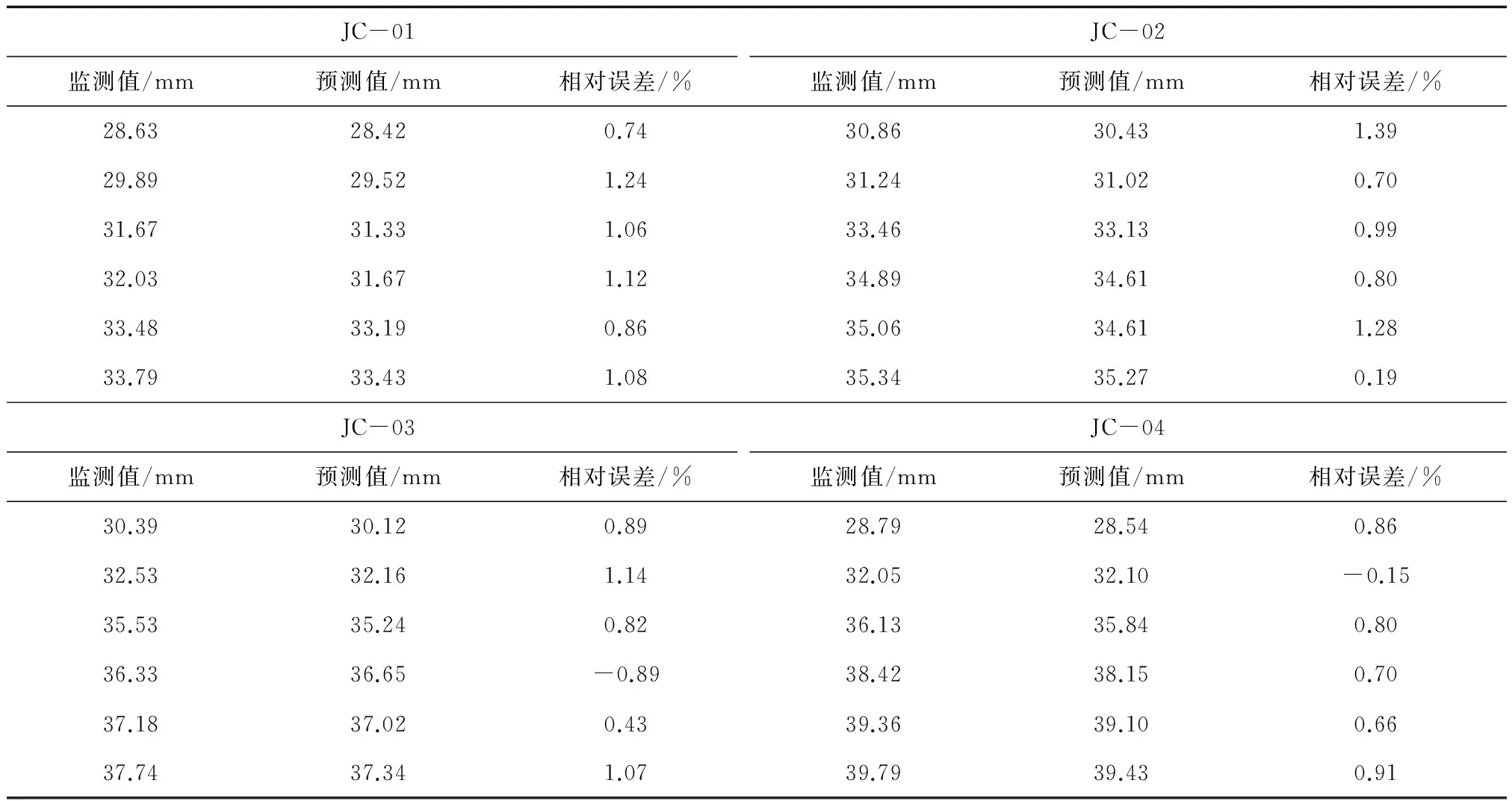
表2　滑坡二阶递进预测结果统计

由表2可知，不同监测点在不同周期节点的预测值具有一定的差异，相对误差多在0～2%之间。在JC-01监测点的预测结果中，最大相对误差为1.24%，最小相对误差为0.74%；在JC-02监测点的预测结果中，最大相对误差为1.59%，最小相对误差为0.19%；在JC-03监测点的预测结果中，最大相对误差为1.14%，最小相对误差为-0.89%；在JC-03监测点的预测结果中，最大相对误差为0.91%，最小相对误差为-0.15%。综合得出二阶递进预测模型具有较高的预测精度，验证本文预测模型的有效性。

2.4不同阶段预测结果分析

本文采用相对误差的期望及方差来评价预测模型，期望用于评价预测模型的精度，方差用于评价模型的稳定性，通过对各个阶段预测结果的统计，结果如表3所示。

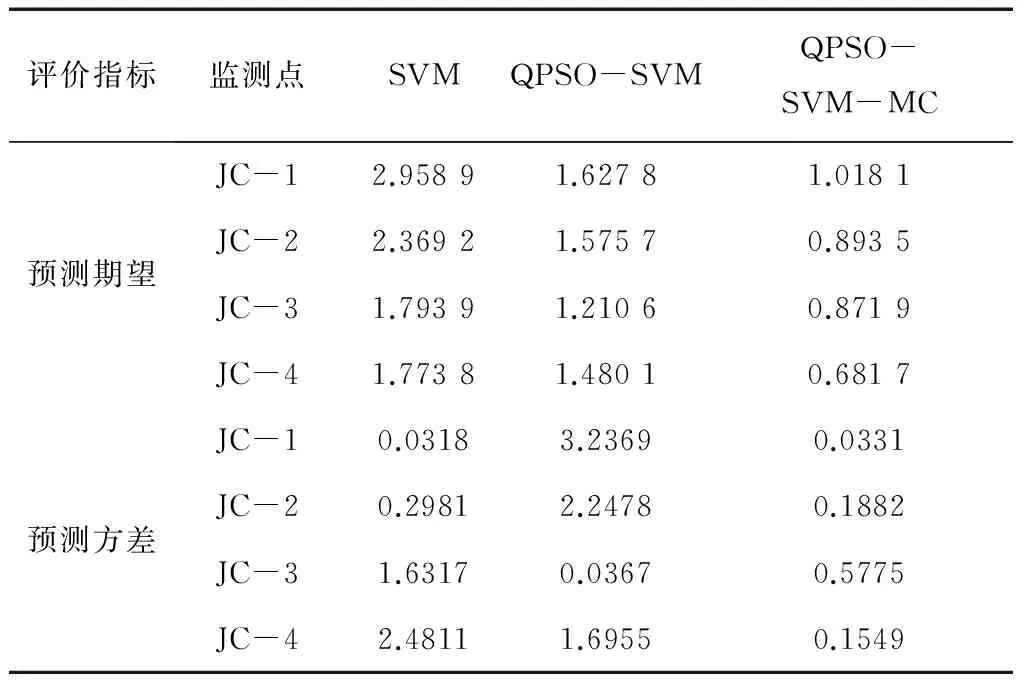
表3　不同预测模型结果对比

由表3可知，在预测相对误差期望方面，不同监测点均表现出随预测阶段的递进，期望值越小，说明预测精度随递进预测，精度得到提高，其中最小预测相对误差在JC-04，期望值为0.681 7，且不同监测点在不同预测模型中的预测效果也具有一定的差异；在预测相对误差方差方面，不同监测点在不同预测模型中的值也具有一定的差异，但在QPSO-SVM-MC预测模型中，各监测点的预测方差均较小，验证本文递进预测模型的有效性。

3　结论

1)通过利用量子算法和粒子群算法对支持向量机预测模型的优化，提高预测精度，得出本文量子粒子群优化支持向量机预测模型的有效性。

2)通过利用马尔科夫链对上一阶段预测误差的修正，建立MC误差修正模型，得出修正后的预测相对误差多在0～2%之间，进一步有效提高预测精度。

3)通过多阶段不同预测模型的组合，利用递进预测的思路，有效减小相对误差，并增加预测结果的稳定性，为滑坡的变形预测提供一种新的思路。

[1]黄发明,殷坤龙,张桂荣,等. 多变量PSO-SVM模型预测滑坡地下水位[J]. 浙江大学学报(工学版),2015(6):1193-1200.

[2]赵艳南,牛瑞卿,彭令,等. 基于粗糙集和粒子群优化支持向量机的滑坡变形预测[J]. 中南大学学报(自然科学版),2015(6):2324-2332.

[3]杨虎,吴北平,陈美华,等. 基于粒子群优化的WA-SVM模型在滑坡位移预测中的应用[J]. 安全与环境工程,2014(4):13-18.

[4]张俊,殷坤龙,王佳佳,等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J]. 岩石力学与工程学报,2015(2):382-391.

[5]谭龙,陈冠,王思源,等. 逻辑回归与支持向量机模型在滑坡敏感性评价中的应用[J]. 工程地质学报,2014(1):56-63.

[6]李越超. 基于QPSO-LSSVM的边坡变形预测[J]. 山地学报,2015(3):374-378.

[7]刘超云,尹小波,张彬. 基于Kalman滤波数据融合技术的滑坡变形分析与预测[J]. 中国地质灾害与防治学报,2015(4):30-35.

[责任编辑：张德福]

Research on the application of progressive prediction model to landslide deformation prediction

CHEN Wei

(Shaanxi Railway Institute，Weinan 714000，China)

In order to improve the landslide deformation prediction accuracy, this paper uses the quantum algorithm and particle swarm optimization algorithm to optimize the support vector machine, and the Markoff chain to correct the error of landslide deformation, and constructs the progressive prediction model of landslide deformation. The results show that: the quantum algorithm and the particle swarm algorithm of support vector machine can be optimized to overcome the difficulties in selecting the parameters of support vector machine and to realize the prediction process of global optimization. After MC error correction model is used to predict of landslide deformation value of the error correction, it can improve the prediction accuracy and predictive value of stability, verify the feasibility and effectiveness of the prediction model, and provide a new prediction method for the prediction of the deformation of landslide.

landslide; support vector machine; particle swarm optimization; error correction

10.19349/j.cnki.issn1006-7949.2016.11.008

2015-12-21

谌伟(1976-)，男，讲师,硕士.

P642.2;TU196

A

1006-7949(2016)11-0038-05