开缝式圆管压电超声换能器研究
刘世清, 陆志刚, 樊叶萍, 李凤鸣
(浙江师范大学 物理与电子信息工程学院,浙江 金华 321004)
0 引 言
超声换能器作为功率超声振动系统的核心组成部分,其作用是产生大功率超声振动能量并加以利用[1-2].针对不同应用需求,需要设计不同结构的超声换能器.在液体超声处理技术领域,目前应用较广的浸没式超声换能器主要有圆管或圆柱型等几种结构类型[3-8].此类换能器主要通过大功率纵向振动压电超声换能器激励金属圆管或圆柱的一端,使之产生径向振动辐射超声能量.这种纵向→径向振动模式转换是通过泊松效应实现的,因而圆管或圆柱的径向振动振幅较小,且波长较长,其辐射声场均匀性及辐射效率有待进一步提高.
相比于纵向振动,弯曲振动振子的声辐射效率较高.基于此,本文提出一种开缝式圆管复合压电超声换能器,其由大功率夹心式压电换能器、变幅杆及开缝式金属圆管纵向复合而成,通过在圆管壁上开狭缝的方式将超声换能器的基频纵向振动转换为圆管壁的高阶弯曲振动,以实现声能辐射.本文对这种开缝式圆管复合压电换能器的弯曲振动特性开展了理论和数值仿真分析.该弯曲振动辐射超声换能器不仅波峰数密度大,而且具有较大的位移振幅,特别适合于超声降解、乳化及声化学反应等液体介质处理技术领域.
1 换能器结构及振动分析
图1所示为一种新型结构的开缝式圆管复合压电超声换能器.该换能器由大功率夹心式压电超声换能器、阶梯型变幅杆、开缝金属圆管振子纵向复合而成.金属圆管壁沿其长度方向均匀透开了一系列平行狭缝,其一端在换能器变幅杆纵向激励下,圆管管壁将作高阶横向弯曲振动,从而实现声能的径向辐射.由于纵向夹心式换能器的设计理论比较成熟,本文基于谐振设计原理,首先对开缝圆管壁及其端盖的弯曲振动特性进行单独理论研究,进而对复合换能器的振动特性进行数值仿真分析.
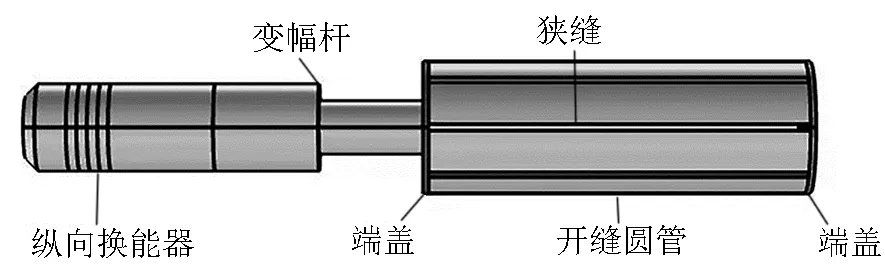
图1 开缝式圆管复合压电超声换能器结构示意图
2 开缝圆管振子的弯曲振动
2.1 圆形端盖的弯曲振动
换能器阶梯型变幅杆输出端与开缝薄壁圆管底部的端盖相固连,端盖为薄圆盘结构,在变幅杆轴向激励下作平面弯曲振动,并将之转换为圆管壁的高阶次横向弯曲振动.为简化处理,将其隔离出来进行单独研究,如图2所示.
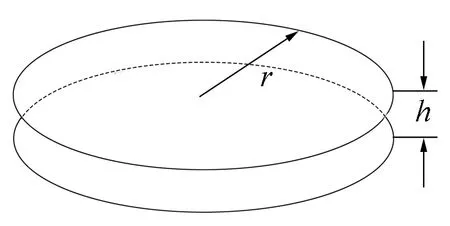
图2 开缝圆管端盖图示
当圆管端盖厚度甚小于其直径(一般厚径比≤1/5),可将其近似为薄圆盘.在此假设条件下,薄圆盘(薄板)的剪切及扭转惯性可以忽略.对于厚度和半径分别为h和r的端盖,其平面弯曲振动的微分方程为[9]
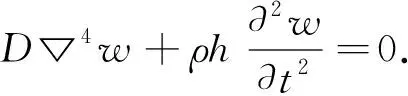
(1)
式(1)中:w为薄板的挠度;设k4=ρhω2/D,ω为圆频率,D=Eh3/[12(1-σ2)]为材料的弯曲刚度;E为材料的弹性模量;ρ为材料密度;σ为材料泊松比.式(1)通解为
w(r,t)=[AJ0(kr)+BY0(kr)+CI0(kr)+
DK0(kr)]ejωt.
(2)
式(2)中:J0(kr),Y0(kr)分别为零阶第一类和零阶第二类贝塞尔函数;I0(kr),K0(kr)分别为零阶第一和第二类修正贝塞尔函数.由于薄圆盘作弯曲振动时,其中心r=0处横向位移为有限值,因此系数B,D均为零,即式(2)可写作
w(r,t)=[AJ0(kmr)+CI0(kmr)]ejωt.
(3)
下标m为振动阶次.对于简支边界下薄圆盘的面内弯曲振动,其边界处的挠度w及弯矩M均为零,即
w(r)=0;M(r)=0.
(4)
由式(3)~式(4)得
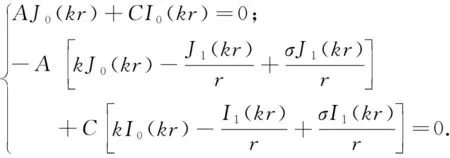
(5)
由式(5)可得到简支边界条件下薄圆盘的弯曲振动共振频率方程为
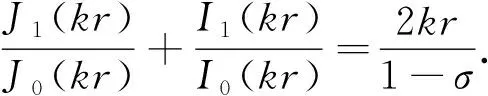
(6)
令式(6)的解为βm,即βm=kmr,则简支边界条件下弯曲振动圆盘的第m阶共振频率为
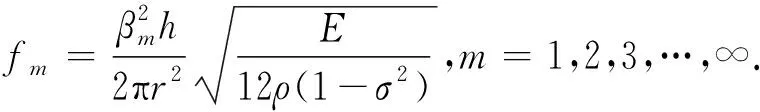
(7)
2.2 管壁弧形条的弯曲振动
如图3、图4所示,开缝圆管即为在管壁上沿长度方向等弧间隔透开一系列狭缝而成.假设管壁厚度较小,且开缝数目足够多,则每一弧形长条可近似作为一细长的等截面矩形截面梁来处理.
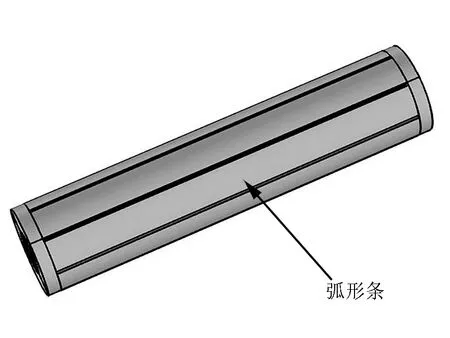
图3 开缝圆管结构图示 图4 弧形条单元图示
由于圆管底部端盖在换能器阶梯型变幅杆驱动下产生平面弯曲振动,与其相连的各弧形条将受到横向弯矩作用而产生弯曲振动,各质点位移方向沿径向.由于弧形条长度远大于其横向尺寸,故可采用Euler-Bemoulli梁理论对其横向弯曲振动进行分析.理论分析中忽略转动惯量和剪切形变的影响,仅考虑弯曲加速度和力的平衡,则有

(8)
式(8)中:Q=∂M/∂x为剪力;M=-EI∂θ/∂x为弯矩;θ=∂w/∂x为挠度角;w为挠度;E为材料的弹性模量;I为转动惯量;S为梁的横截面积.将表达式代入式(8),分离变量并不考虑时间项得
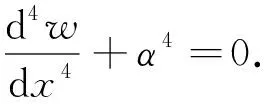
(9)
式(9)中,
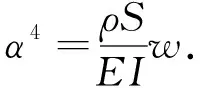
(10)
式(9)的通解为
w=Acos(αx)+Bcosh(αx)+
Csin(αx)+Dsinh(αx).
(11)
对于两端简支的等截面梁,其边界处的挠度w及弯矩M均为0,即
w(0)=0;w″(0)=0;w(L)=0;w″(L)=0.
(12)
由式(11)及边界条件式(12)得
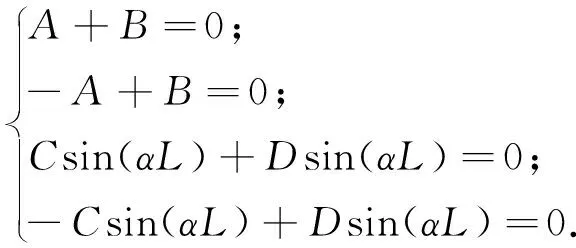
(13)
由式(13)得两端简支等截面梁的弯曲振动共振频率方程
sin(αL)=0.
(14)
令式(14)的解为γn,即γn=αnL,n为振动阶次.由此得固有频率的表达式为
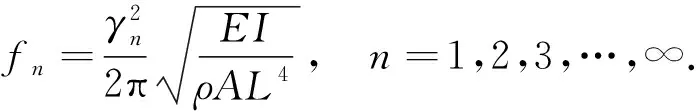
(15)
频率方程反映了振子的共振频率与其材料及几何尺寸之间的相互依赖关系.给定振子的材料及几何参数即可求出共振频率,或者给定共振频率和材料参数求振子的尺寸.
算例1:在进行振动系统设计时,通常先给定振子的共振频率和材料参数,再依据频率方程求出相应的几何参数.依据上述共振频率方程,对开缝圆管壁及其圆盘端盖的弯曲共振频率进行了理论与数值仿真计算.选取圆管材料为6061Al,材料特性参数如下:密度ρ=2 700 kg/m3,泊松比σ=0.33,弹性模量E=70 GPa;开缝数N=12;表1中的管半径R、管长L、端盖厚度h及理论频率f为给定值;依据频率方程计算得到管壁厚度H与对应的弯曲振动阶次n及相应的共振频率仿真值fe如表1所示.Δ为共振频率理论与仿真值之间的相对误差.由表1可知,开缝圆管振子的高阶弯曲共振频率理论与仿真结果符合较好.
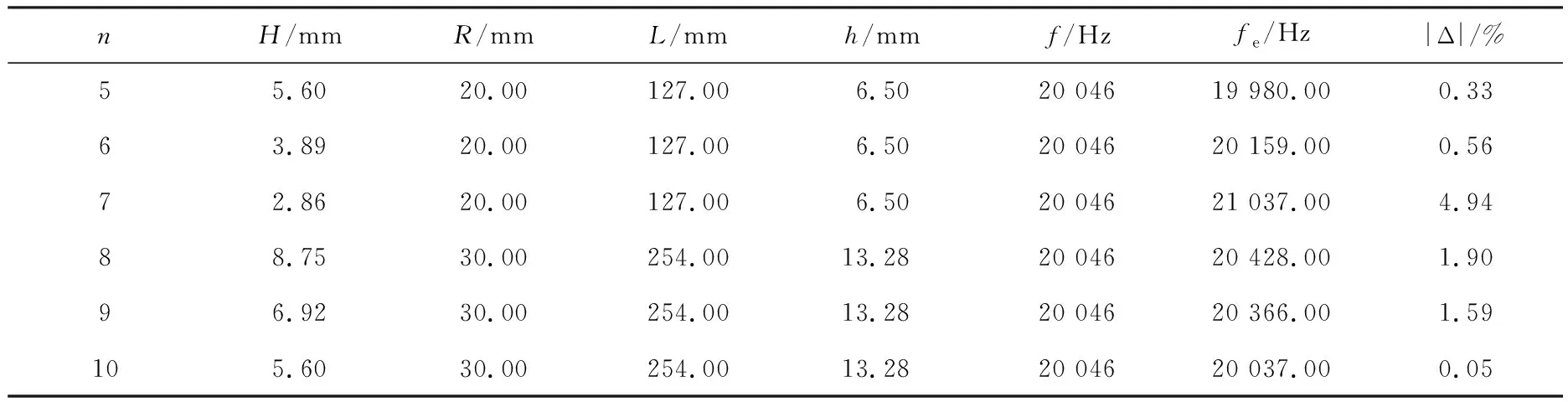
表1 开缝圆管振子弯曲振动共振频率理论与仿真结果
3 数值仿真
3.1 开缝圆管弯曲振动频率特性
共振频率是振动系统的重要特性参量,其依赖于振子的材料及几何参数.为探究开缝圆管半径、长度、管壁厚度及端盖厚度对其振动特性的影响,利用COMSOl Multiphysics有限元仿真软件对开缝圆管的尺寸进行参数化扫描,得到弯曲振动共振频率随其几何尺寸变化关系的仿真结果如图5、图6所示.数值仿真计算中材料特性参数如前述给出,圆管壁狭缝数目为10条,狭缝宽2 mm.
由图5、图6可知,开缝圆管的弯曲共振频率随其半径和长度的增大而降低,随其管壁及端盖厚度的增大而升高.

图5 共振频率随管半径的变化关系 图6 共振频率随管壁厚度的变化关系
3.2 换能器振幅特性
位移振幅是振子的重要特性参数之一,如在超声加工、超声波液体处理等领域,总希望工具头或辐射器具有尽可能大的位移振幅,以提高超声能量的传递或辐射效率.以下对开缝圆管振子与夹心式压电换能器组成的复合系统振幅特性进行有限元数值仿真分析.采用谐振组合设计方法,即分别对全波长夹心式压电换能器(含半波长阶梯变幅杆)和开缝圆管辐射器进行仿真设计.仿真建模参数如下:半波长换能器前、后盖板材料为6061硬铝,长度分别为60 mm和25 mm,直径均为50 mm,材料参数如前述;压电陶瓷为PZT-4,尺寸Φ50×Φ25×6,共4片;半波长阶梯变幅杆材料为钢,大端、小端长度均为60 mm,直径分别为50和30 mm;开缝圆管材料为6061硬铝,管长、管径、管壁及端盖厚度分别为254.0,60.0,6.9及13.3 mm; 管壁开缝数为8,缝宽2 mm.在上述给定参数条件下,全波长换能器纵向振动基频共振频率、开缝圆管第9阶高次弯曲谐振频率及二者纵向复合后的换能器的共振频率分别为20 235,20 366和19 232 Hz.
利用 COMSOL 有限元软件对开缝圆管复合压电换能器的振动模态进行了仿真,结果如图7所示.由图7可以看出,换能器与圆管端盖分别工作于基频纵向振动模式和第1阶平面弯曲振动模式,而开缝圆管壁工作于第9阶弯曲谐振模式,且具有较大的波峰数密度和振幅.
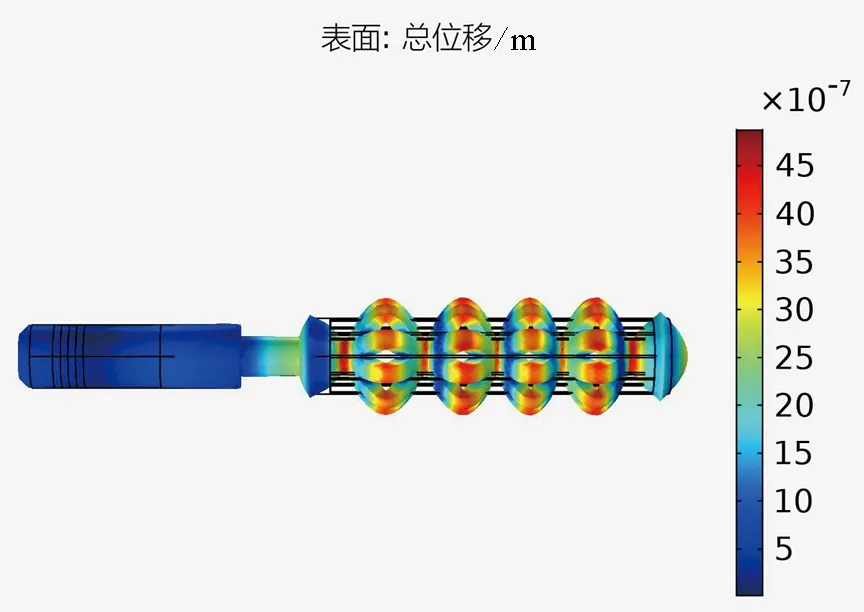
图7 开缝圆管复合压电超声换能器模态振型(f=19 232 Hz)
通过提取复合压电换能器沿轴向的位移振幅分布,结果如图8所示.图8(a)为全波长换能器的轴向位移分布;图8(b)为开缝圆管振子管壁的弯曲振动位移分布.由图8可知,开缝圆管壁的最大弯曲振幅约为换能器变幅杆输出端纵向最大位移振幅的2倍.可见,通过开狭缝的方式可提高换能器输出端的位移振幅,从而可较大幅度提高此类换能器在介质中的声辐射效率.
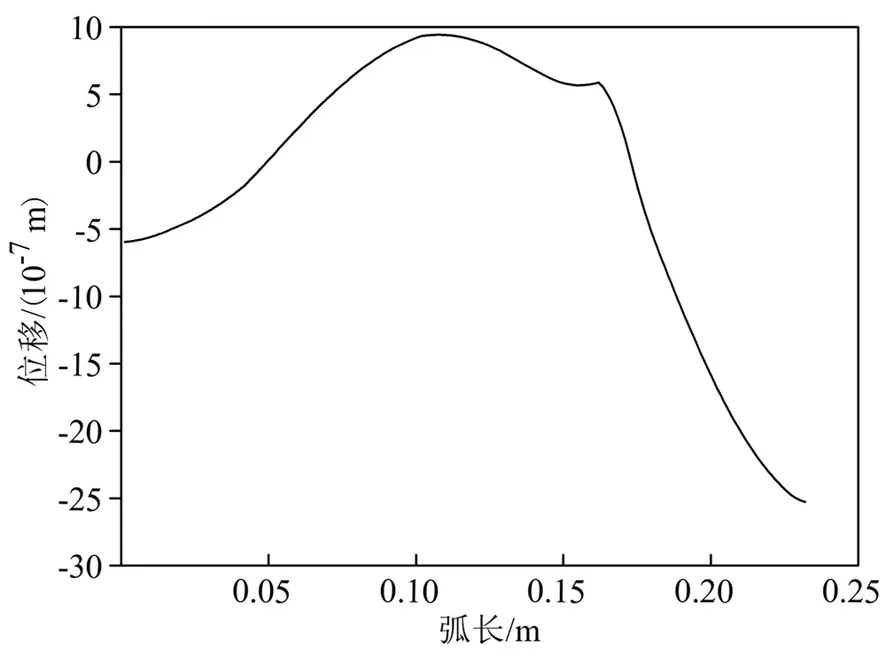
(a)换能器轴向位移分布
显然,作为浸没式液体处理超声换能器,振动时较大的体积形变量意味着更高的声辐射效率.为此,通过有限元法提取开缝圆管辐射器前10阶弯曲谐振下的表面振动位移,并对振子表面积分得到其体积形变量随振动阶次的变化关系如图9所示.
由图9可以看出,开缝圆管的体积形变量并非随其振动阶次的升高而增大,而是存在一极大值.对于本文研究的开缝圆管,其体积形变量极大值对应的弯曲振动阶次为第4、第5阶.进一步通过有限元分析发现,在相同的换能器驱动载荷下,开缝圆管辐射器的最大体积形变量约为同尺寸无缝圆管辐射器的3倍,意味着通过管壁开狭缝的方式能较大幅度地提高圆管型压电超声换能器的声辐射效率.

图9 开缝圆管弯曲振动体积形变量与振动阶次n的关系
4 结 论
本文对一种新型的纵弯振动模式转换开缝式圆管压电超声换能器的振动特性进行了理论和有限元数值仿真研究,给出了圆管端盖平面弯曲振动及管壁弧形单元的横向弯曲振动频率方程.对开缝圆管的弯曲振动共振频率与其几何尺寸的关系进行了有限元仿真研究,并对开缝圆管复合压电超声换能器的振幅特性进行了数值仿真分析,研究结果表明:
1)开缝圆管的弯曲振动共振频率随其半径和长度的增大而降低,而随其管壁及端盖厚度的增大而升高.
2)弯曲振动具有振幅放大作用,本文研究的开缝圆管最大弯曲振幅约为其激励端变幅杆最大纵向振幅的2倍;其振动体积形变量约为相同驱动载荷下同尺寸无缝圆管的3倍.
3)开缝圆管体积型形变量随其振动阶次的变化存在极大值,并非振动阶次越高体积形变量越大.
此外,本文研究的开缝式圆管复合压电超声换能器不仅具有较高的弯曲波振幅,而且具有较高弯曲波峰数密度与较大的体积形变量.因此,弯曲振动振子的声辐射效率较高,在超声清洗、水处理及声化学等液体处理领域极具应用前景.

