开缝蜂窝结构电磁/力学综合性能设计
杨森 ,陈海燕 ,郏亚威,姚鑫,孙启峰
(1.国家电磁辐射控制材料工程技术研究中心,四川 成都 611731;2.多频谱吸波材料与结构教育部重点实验室,四川 成都 611731;3.电子科技大学,四川 成都 611731)
蜂窝吸波材料具有密度小、重量轻、强度高[1-2]和吸波性能优异等特点,被广泛应用在航空航天、建筑、交通等领域。随着蜂窝吸波材料研究的不断进展,涌现出很多的新型蜂窝复合结构,包括填充型[3]、嵌入型[4]、串联型[5]、层次性[6]、负泊松比型[7]、负刚度[8]等。在过去的二十多年,国内外对蜂窝材料在不同加载条件下的基本力学响应,包括拉伸、压缩、屈曲、剪切和疲劳做了大量研究[9-12]。多功能蜂窝复合材料,如吸波蜂窝复合材料的研究也有长足发展。如罗辉等[13-14]设计的一种双层吸波结构,蜂窝上表面加匹配层作为阻坑匹配,蜂窝下表面加吸收层得到的蜂窝夹层结构具有轻质及宽带吸收的特点。Kwak 等[15]设计的双蜂窝芯三层蒙皮的镀镍玻璃织物蜂窝夹层结构,扩大了吸波入射角范围。总的来说,蜂窝吸波复合材料在朝着轻质、高强度及更好吸收性能的方向发展,蜂窝吸波结构的多功能设计有待进一步研究。
为了满足蜂窝吸波材料多功能的应用,在蜂窝内部嵌入天线和雷达等电子模块器件,出现了基于蜂窝夹层板进行预埋的设计方法,最早在20 世纪90 年代由洛克希德马丁航天公司在进行多功能结构设计中提出[16]。即将蜂窝芯局部挖空,把高度集成的电子模块埋入芯内部并进行保护加固设计,使航天器的设计在轻量化方面有了质的飞跃。毕中臣等[17]对蜂窝纸板进行开槽处理,结果表明开槽可以降低其起始屈服应力,提高蜂窝平台区的缓冲性能。马科峰等[18]从实验角度研究了传统芳纶纸蜂窝芯、开槽芳纶纸蜂窝芯以及有孔芳纶纸蜂窝芯的主要力学性能。夏明凯等[19]用数值模拟的方法对金属蜂窝夹层板侧压强度和破坏模式的影响进行了研究。上述研究都针对蜂窝的力学方面,结果表明开缝蜂窝的力学性能有所降低。而对于开缝蜂窝的电磁性能,国内外的研究较为鲜见,开缝蜂窝的电磁/力学综合设计有待深入研究。
本文在完整蜂窝的基础上对其进行开缝处理的设计,研究了其开缝后电磁/力学性能的变化。力学方面主要研究在单轴静态压缩下,开缝率对蜂窝结构力学的位移载荷关系特性的影响;电磁方面主要探究不同类型开缝对蜂窝结构X 波段两种极化下吸波性能的影响。
1 开缝蜂窝结构的力学性能
蜂窝结构单元为一种正六边形单元周期结构,如图1 所示。L为蜂窝的L 方向的长度,W为蜂窝W 方向的长度,T为蜂窝的高度,L1为蜂窝的边长,t为蜂窝壁的厚度,θ为蜂窝壁的夹角。

图1 (a)Nomex 蜂窝实物图;(b) Nomex 蜂窝的参数示意图Fig.1 The sample of the Nomex honeycomb.(a)Physical picture;(b) Dimention parameters
Nomex 蜂窝比较柔软,尺寸较小,很难开出规则形状,本文从仿真角度研究开缝蜂窝的力学性能。仿真参数L=60 mm,W=60 mm,T=20 mm,L1=1.83 mm,t=0.1 mm,θ=120°。
在完整模型的基础上,开5 个相同的缝隙,如图2(a)所示,L2为缝隙的长度,W2为缝隙的宽度,T2为缝隙的高度。共9 种缝隙,缝隙长度L2分别为10,30,50 mm,缝隙宽度W2分别为2,4,6 mm,缝隙高度T2都是20 mm。
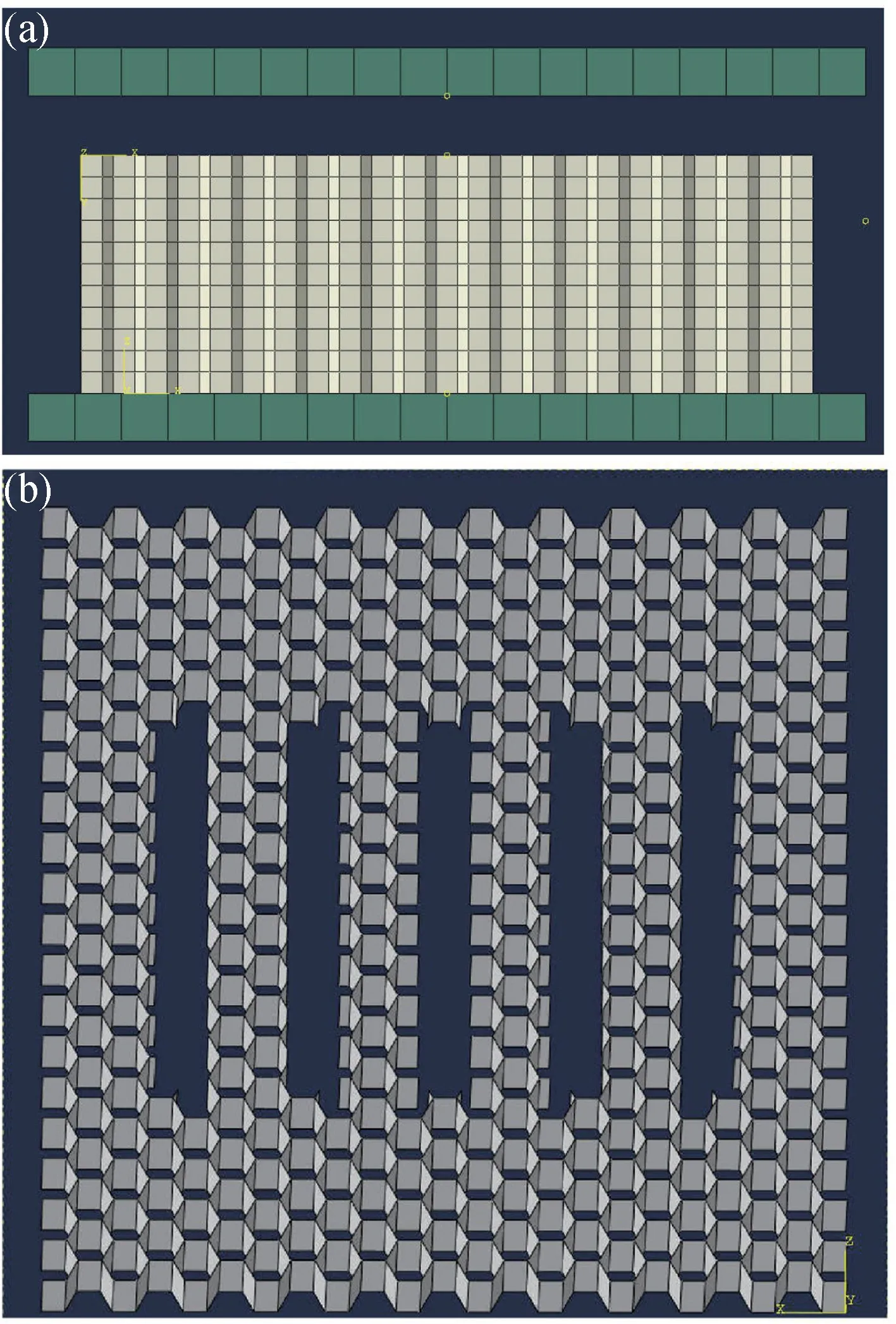
图2 (a)仿真模型图;(b)开缝蜂窝模型Fig.2 The Nomex honeycomb model.(a) Simulation model;(b) Slotting details
用有限元分析软件LS-DYNA 对蜂窝结构在压缩下的力学性能进行仿真。首先对蜂窝结构进行整体建模,先建立单蜂窝模型,然后进行旋转复制和布尔运算,得到蜂窝模型;再建立5 个长方体模型,通过相减,得到开缝蜂窝的模型,如图2(a)所示。为了模拟实验条件,蜂窝上下面各设定一个刚体,上刚体以恒定速度v向下移动,下刚体固定不动,如图2(b)所示。蜂窝材料采用弹塑性材料[20-22]模型,蜂窝材料参数为: 密度0.66×10-3g/mm3;弹性模量4400 MPa;泊松比0.3;屈服强度80 MPa。蜂窝整体接触属性设置为自接触,刚体与蜂窝的接触为面面接触;LSPREPOST 专用后处理软件,提取反作用力和观察压缩过程中的变形。
如图3 所示,开缝尺寸为2 mm×30 mm×20 mm 的位移-载荷曲线,开缝蜂窝压缩的过程可以分为三个阶段[23-25]。第一阶段AB 段,呈线性,此阶段蜂窝处于弹性形变阶段,其斜率为蜂窝T 方向的弹性模量。B 点是弹性形变的峰值点,蜂窝在B 点屈服,弹性阶段积累的能量由于蜂窝屈服破坏而瞬间释放,载荷有明显下降,一般把B 点称为蜂窝的屈服强度。第二阶段CD 段,蜂窝进入塑性形变阶段,此阶段蜂窝壁弯曲渐进折叠,载荷在一定范围内小幅变化,蜂窝吸收能量主要在塑性变形CD 段。第三阶段DE 段是致密化阶段,蜂窝孔壁完全折叠,蜂窝结构彻底破环。
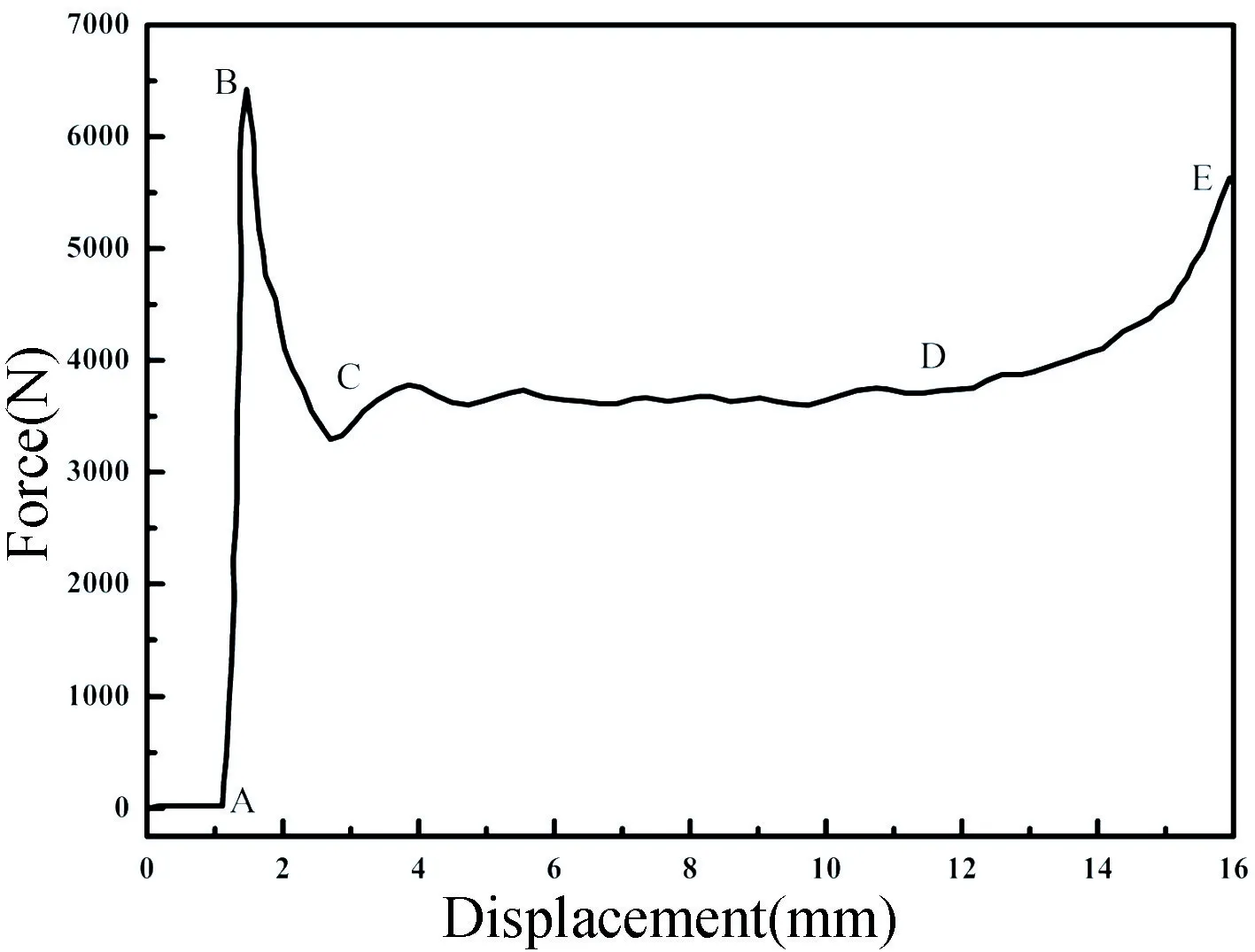
图3 开缝尺寸2 mm×30 mm×20 mm 蜂窝的位移-载荷曲线Fig.3 Load-displacement curve of the honeycomb with the slotting size of 2 mm×30 mm×20 mm
如图4 为仿真得到9 种开缝结构的位移-载荷曲线,其中,No-slot 代表没有开缝的蜂窝,Slot-W2-L2表示缝隙的宽度和长度。
由图4 可知,在准静态平面压缩载荷下,蜂窝开缝后的力学性能有较大变化,位移载荷曲线向下偏移,说明蜂窝开缝后的屈服强度、平均平台应力减小;随着开缝尺寸增加,蜂窝的弹性模量基本不变,屈服强度、平均平台应力、比吸能减小。值得注意的是,开缝蜂窝在准静态压缩过程中的曲线的三个形变阶段仍然保持一致。
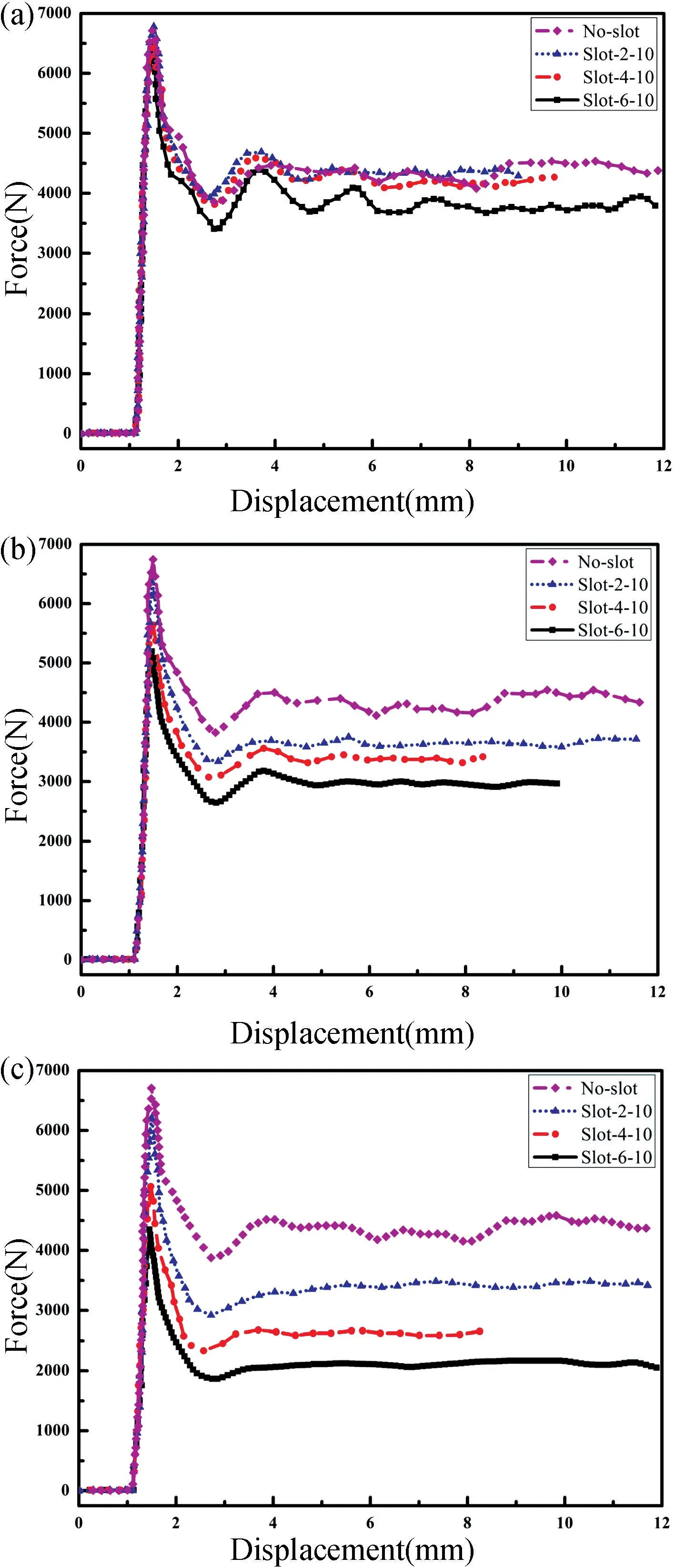
图4 不同开缝蜂窝的位移-载荷曲线。(a)开缝长度10 mm;(b)开缝长度30 mm;(c)开缝长度50 mmFig.4 Load-displacement curves of the slotted honeycombs with various slotting length.(a) Slotting length is 10 mm;(b) Slotting length is 30 mm;(c) Slotting length is 50 mm
由图4 可以建立开缝尺寸与开缝蜂窝静态压缩屈服强度、平均平台应力之间的关系,以此评估其他开缝尺寸参数下蜂窝的抗压能力。如表1 是由仿真计算得到的不同开缝尺寸蜂窝平面压缩的峰值应力和平均平台应力。
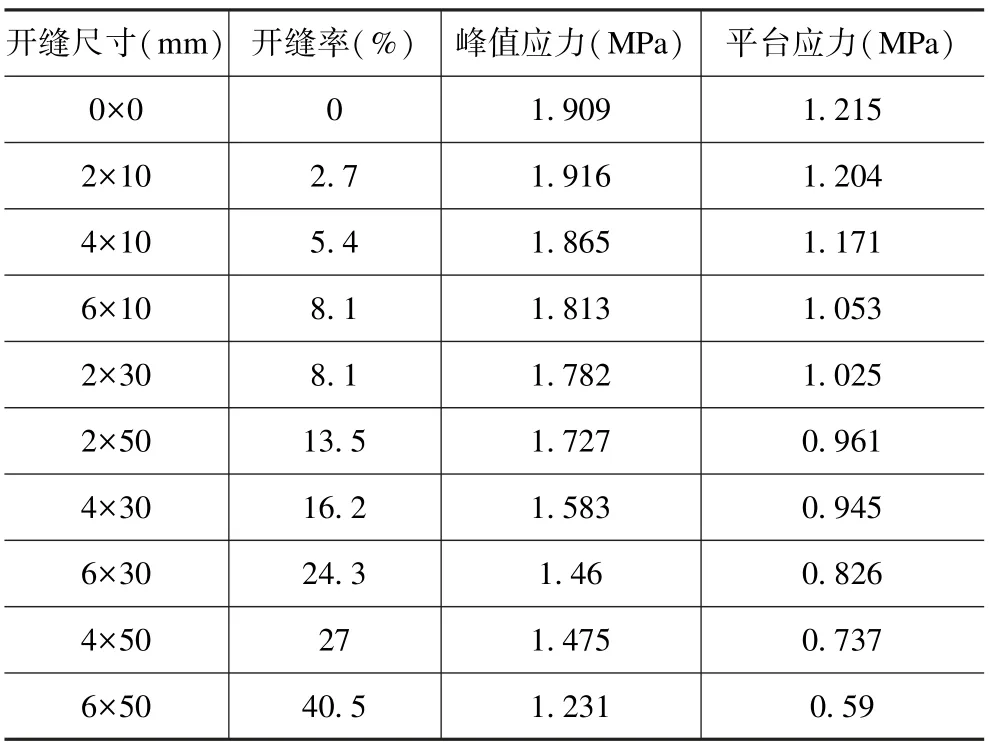
表1 9 种开缝尺寸的峰值应力和平均平台应力的值Tab.1 Simulated peak and plateau stress values of the Nomex honeycomb with variable slotting sizes
由图4(a)可知,没有开缝、开缝尺寸2 mm×10 mm 和开缝尺寸4 mm×10 mm 的三条曲线相互交叉,变化很小;由表1 可知,开缝率为5.4%时,峰值应力下降2.3%,平台应力下降3.6%。开缝率在5.4%之内时,开缝蜂窝的峰值应力和平台应力变化很小;开缝率超过5.4%后,峰值应力和平台应力随开缝率的增大明显减小,呈直线下降。从拟合曲线预测任意尺寸开缝蜂窝的峰值应力和平台应力,再根据无缝蜂窝的弹性模量,就可以模拟出任意尺寸开缝蜂窝的位移-载荷曲线,从而评估开缝蜂窝单轴平面压缩的力学性能。
对上述开缝蜂窝的仿真模型及结果进行实验验证。实验所用蜂窝如图1(a),蜂窝参数与仿真参数保持一致。所用实验仪器为万能拉力试验机,在常温常压下进行单轴平压实验,设备压头上面放置压力传感器,压头匀速向下运动,速度2 mm/min,实验获得位移-载荷曲线,结果如图5 所示。
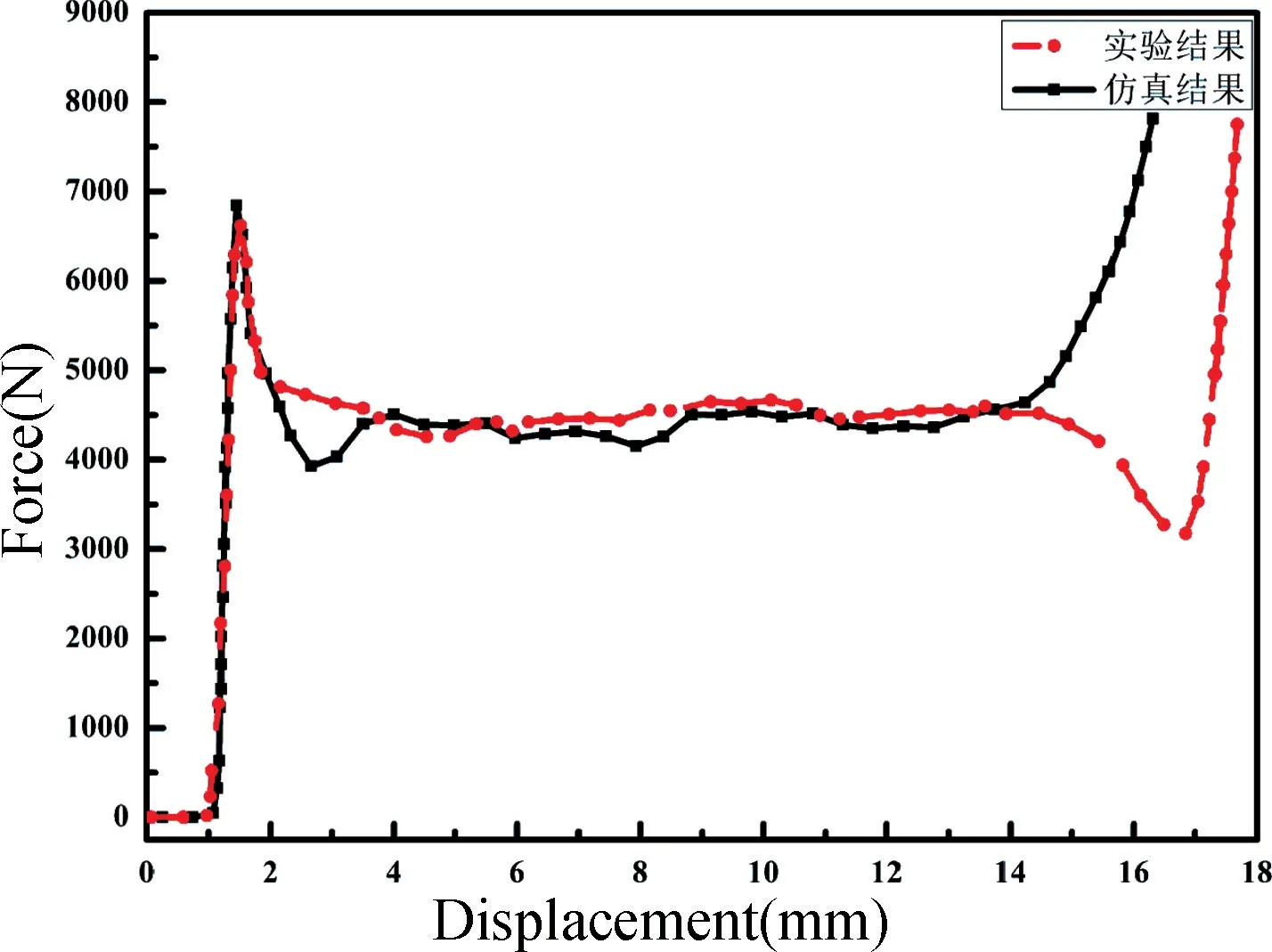
图5 实验和仿真的位移-载荷曲线Fig.5 Experimental and simulated load-displacement curves of the considered honeycomb structures
从图5 可以看出,实验获得的位移-载荷曲线和仿真曲线吻合较好,蜂窝压缩过程中的三个阶段一致,验证了所建立的蜂窝平压仿真模型的正确性,可以通过该仿真方法模拟实验来得到开缝蜂窝的位移-载荷曲线,从而分析其力学性能。对比图3 和图5,开缝蜂窝与无缝蜂窝的位移-载荷曲线的三个阶段保持一致,表明开缝蜂窝在重量减轻的同时,与无缝蜂窝单轴平压力学特性类似。
2 开缝蜂窝结构的电磁性能
2.1 不同开缝长度
为实现蜂窝的电磁/力学综合设计,开缝蜂窝的电磁模型在开缝参数上需与力学模型保持一致,即蜂窝分别以不同的长度、宽度及高度开缝,本节研究缝隙的尺寸(开缝长度和宽度)对电磁性能的影响。
蜂窝是以正六边形胞元为基本单元的周期结构,根据蜂窝的等效电磁参数理论,把浸渍吸波涂层的Nomex 蜂窝结构当成吸波平板,赋予吸波材料的属性,在平板上进行开缝。吸波材料介电常数的实部和虚部如图6 所示。

图6 吸波材料的介电常数Fig.6 Delectric constant of absorber material
用电磁分析软件FEKO 仿真蜂窝结构的单站RCS。蜂窝面板尺寸200 mm×200 mm×10 mm,面板倾斜角22°,θ=90°,φ: 0°~60°,底层加PEC,频率设为X波段三个频点: 8,10,12 GHz,极化方式为线性hh极化和vv 极化。
为研究开缝不同长度对RCS 的影响,蜂窝面板开缝数量为15 个,缝隙尺寸相同,如图7 所示,缝隙宽度w3固定为2.5 mm,缝隙高度均为10 mm,缝隙长度L3分别设计为50,100,150,190 mm。仿真结果如图8 所示。
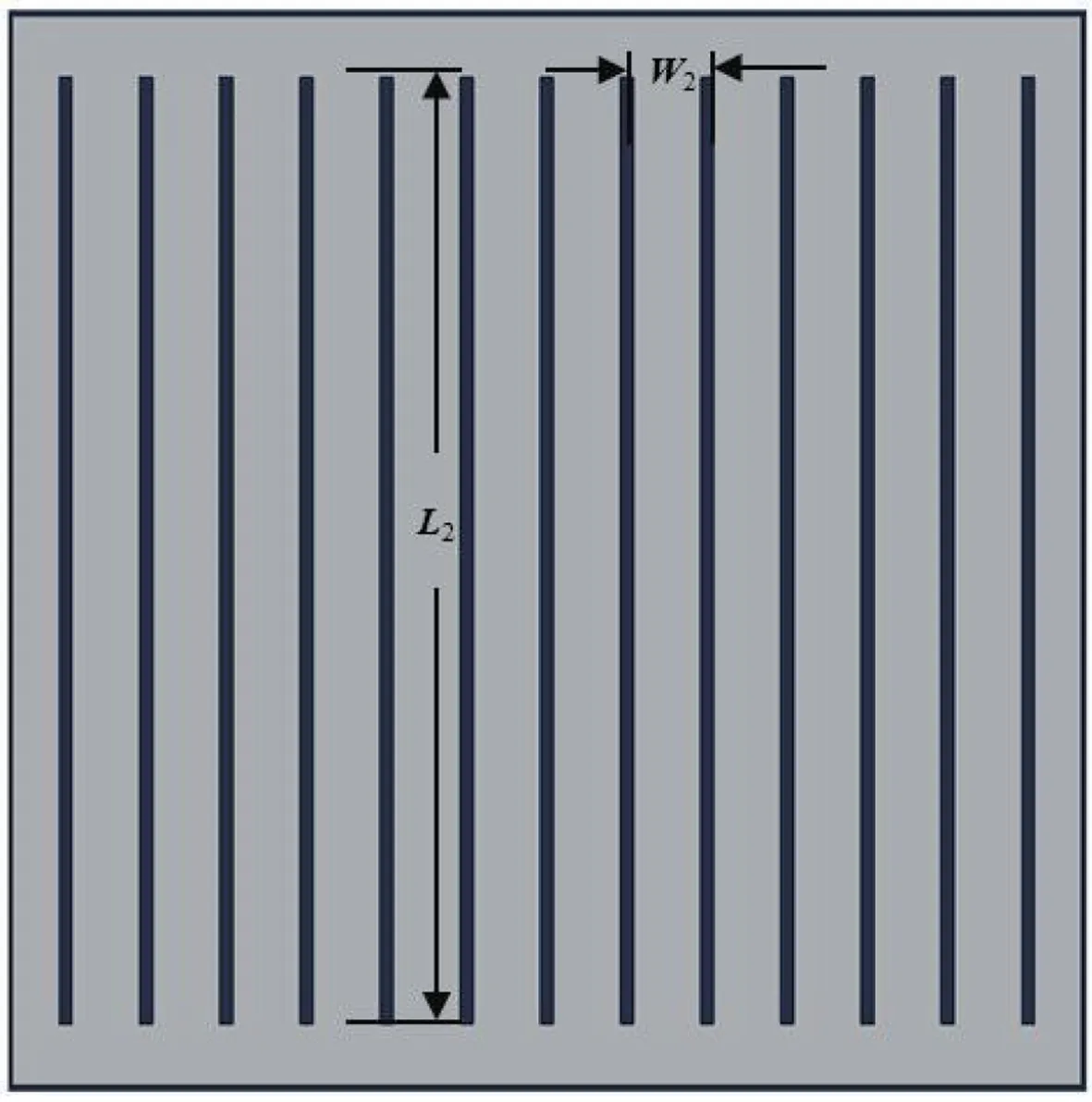
图7 吸波面板开缝模型Fig.7 Slotting model of the absorbing panel
2.2 不同开缝宽度
仿真参数设置与2.1 节一致,开缝尺寸w3分别为2,4,6,8 mm,L3为177.5 mm,高度为10 mm,研究开缝不同宽度对RCS 的影响。如图9 为不同开缝宽度的RCS 仿真结果。
由图8,9 可知,当旋转角φ在小角度时(0°~3°,在此RCS 的值小于-30 dBm2),开缝蜂窝面板在hh 极化,8 GHz 和10 GHz 频率下,吸波性能相较于未开缝蜂窝都有所增加;但在12 GHz 下,不同开缝长度的蜂窝吸波性能均变好,不同开缝宽度时,开缝宽度在2 mm 时性能变好,在4,6,8 mm 时吸波性能变差。而在vv 极化,不同长度开缝和不同宽度开缝的蜂窝,8 GHz 时吸波性能差,10 GHz 时吸波性能好,12 GHz时吸波性能又变差。对于极化而言,不同开缝条件在vv 极化下的吸波性能均高于hh 极化。
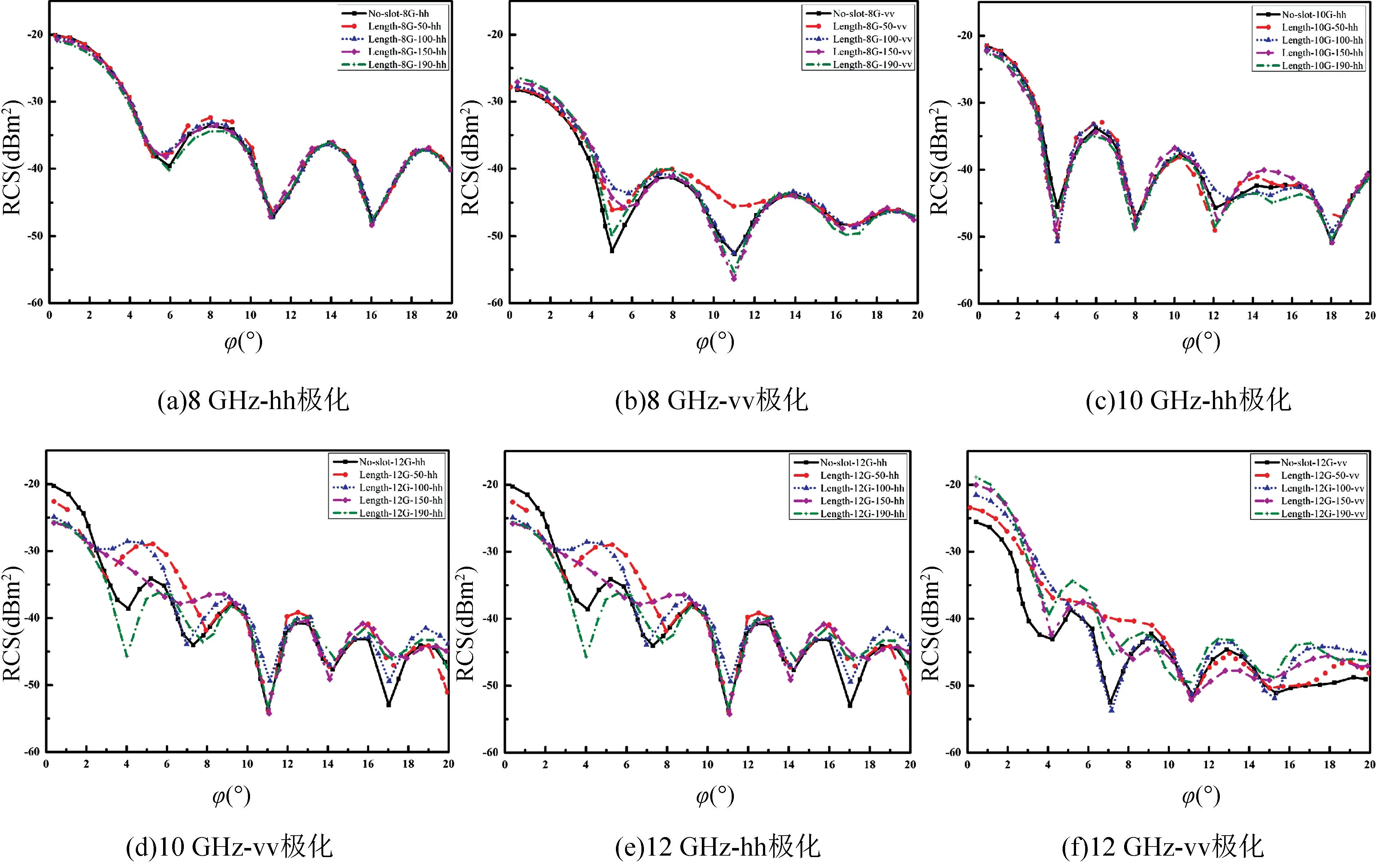
图8 不同开缝长度蜂窝反射率仿真结果Fig.8 The reflectivity of simulation of the honeycomb absorbing structures with variable slotting lengths
图9 不同开缝宽度蜂窝反射率仿真结果Fig.9 The reflectivity simulation of the honeycomb absorbing structures with variable slotting widths
2.3 不同开缝方式
仿真参数设置与2.1 节一致,其中2.1 节和2.2节开缝都是规则开缝,开缝高度都为10 mm。电磁波照射到蜂窝面板上,会有反射和吸收。为了增大电磁波与蜂窝面板的接触,使电磁波在蜂窝内多次反射吸收,达到较好的吸波性能,本节蜂窝上下面板T/2 高度5 mm 开不同的缝隙。蜂窝面板开缝数量为15 个,第一种开缝方式为: 第一个面板不开缝,作为对照组;第二个面板规则开缝,开缝尺寸为177.5 mm×2.5 mm×10 mm,作为对照组;而第三个面板开缝上下不同缝长,其中上缝: 177.5 mm×2.5 mm×5 mm,下缝:1.5.5mm×2.5 mm×5 mm;第四个面板开缝上下不同缝宽,上缝: 177.5 mm×2.5 mm×5 mm,下缝: 177.5 mm×8 mm×5 mm,如图10(a)、(b)所示。第二种开缝方式为: 四个面板同第一种开缝尺寸,第一、第二块面板同第一种开缝方式;第三个面板把第一种开缝方式的上缝长177.5 mm、下缝长185.5 mm 改为上缝长185.5 mm、下缝长177.5 mm,即上下缝长翻转;第四块面板把第一种开缝方式的上缝宽2.5 mm、下缝宽8 mm 改为上缝宽8 mm、下缝宽2.5 mm,即上下缝宽翻转,如图10(b)所示。两种开缝方式的RCS 仿真结果如图11,12 所示。

图10 第一种开缝方式。(a)第三块面板;(b)第四块面板Fig.10 The first slotting way.(a) The 3th panel;(b) The 4th panel
由图11,12 可知,对RCS 值影响最大的是当旋转角φ在小角度(0°~3°)时。对于不同的开缝方式,hh 极化时,8 GHz 和10 GHz 频率下,开缝后吸波性能略有增加;但是12 GHz 时,第一种方式开缝后性能变好,第二种方式开缝后,规则开缝和上下不同缝长,吸波性能变好,上下不同缝宽时,吸波性能变差。而在vv 极化下,对于不同的开缝方式,开缝后8 GHz 时吸波性能变差,10 GHz 时吸波性能变好,12 GHz 时吸波性能又变差。对于极化来说,8 GHz 和10 GHz 时,不同方式开缝后在vv 极化下的吸波性能均高于hh 极化。
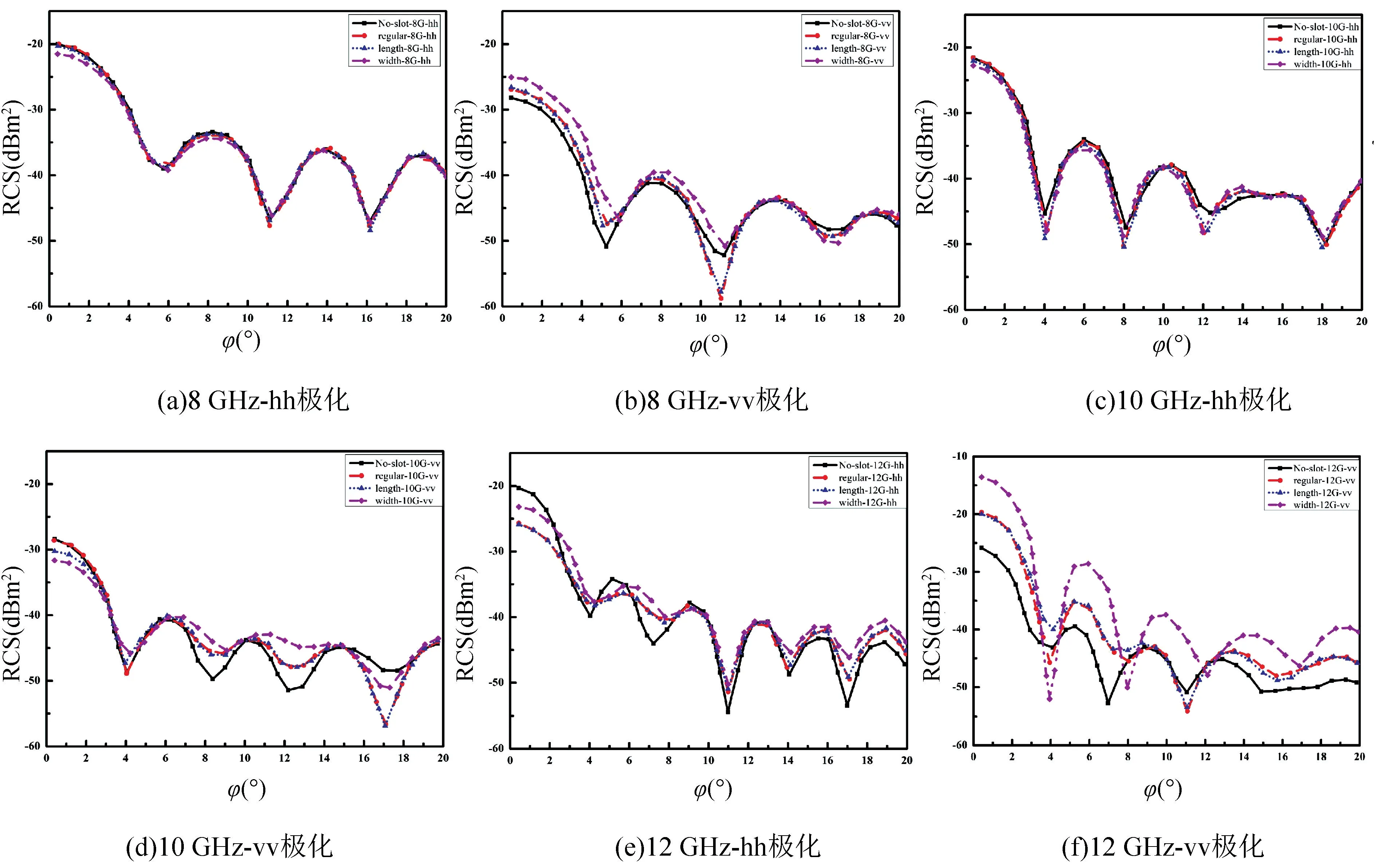
图11 第一种开缝方式仿真结果Fig.11 Simulation results of the honeycomb absorbing structures with the 1st slotting scheme
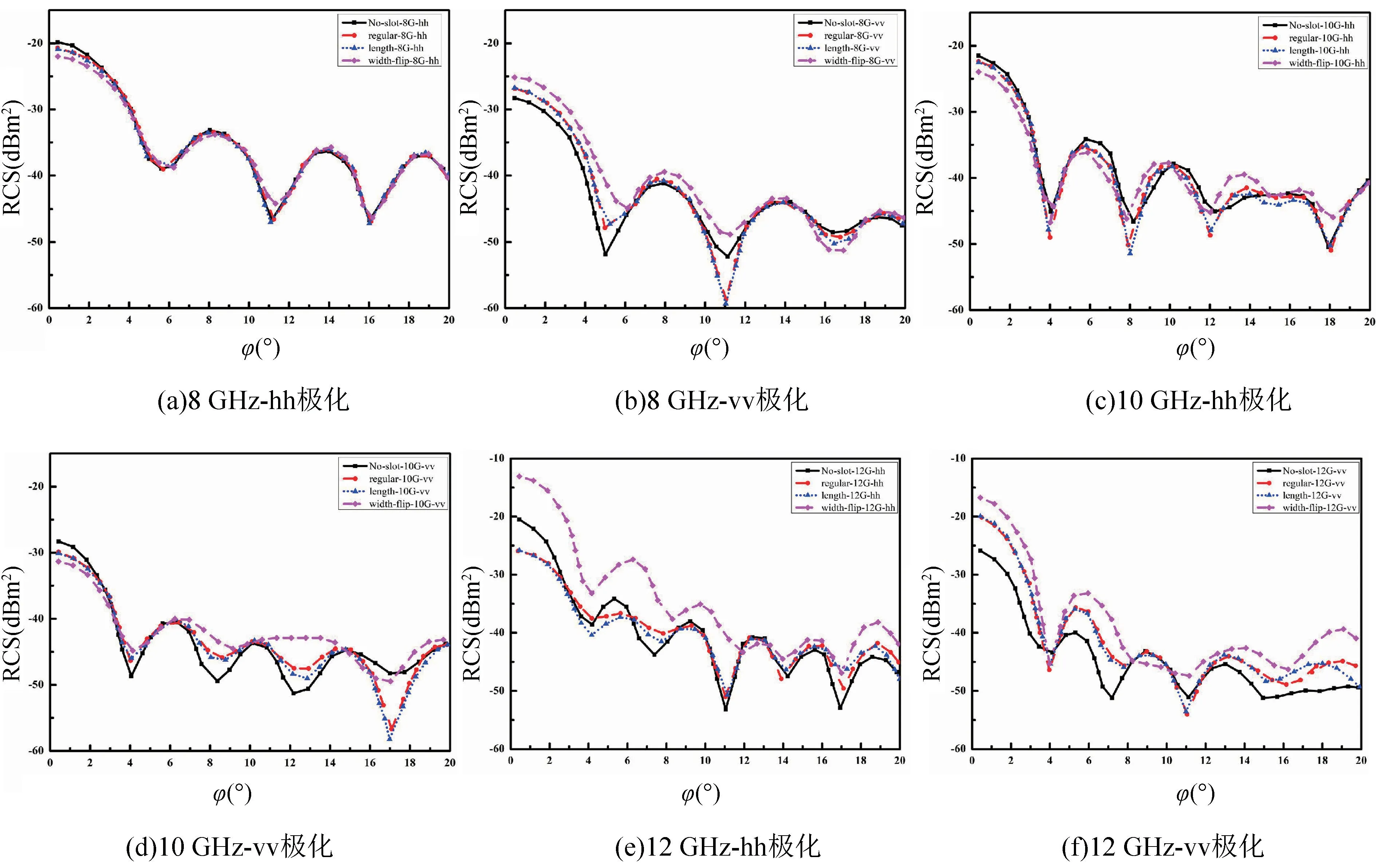
图12 第二种开缝方式仿真结果Fig.12 Simulation results of the honeycomb absorbing structures with the 2nd slotting scheme
3 结论
本文针对传统蜂窝吸波结构,研究了不同开缝方式对开缝蜂窝吸波结构电磁/力学性能的影响。开缝后的蜂窝在压缩过程中的位移-载荷曲线与传统蜂窝一致,蜂窝开缝率在5.4%之内,开缝蜂窝在压缩下的力学性能变化较小;随着开缝率的增大,其力学性能明显降低。电磁方面,在hh 极化时,8 GHz 和10 GHz频率下,蜂窝开缝后吸波性能都有所增加;vv 极化时,8 GHz 和12 GHz 频率时,开缝后吸波性能变差,10 GHz 时,开缝后吸波性能变好。对于极化来说,8 GHz 和10 GHz 时,蜂窝开缝后在vv 极化下的吸波性能均优于hh 极化。

