一种用于BDD网络可靠性分析的启发式排序新方法
潘竹生, 李闻白, 林飞龙
(1.浙江师范大学 数学与计算机科学学院,浙江 金华 321004;2.浙江师范大学 经济与管理学院,浙江 金华 321004)
0 引 言
二元决策图即BDD(binary decision diagram)及其扩展型在电路验证[1]、紧凑马尔可夫链表达式[2-4]、编程中对大型元组集的有效处理[5]、符号模型检验[6-8]和各种类型系统[9-11]的可靠性分析等领域有着广泛的应用,因此,快速高效地构建BDD模型成为最近20年的一个研究热点,内容主要包括变量排序研究和模型构建方法研究.
变量排序[12]严重影响BDD模型大小.在极端情况下,不同质量的变量排序对应的BDD模型大小可以跨越几个数量级[13].所以,寻找优质排序是一个非常重要的问题.然而,寻找最优排序是一个NP完全问题[13].在实际应用中,只能采用启发式排序[14-15]策略,如基于广度优先搜索BFS(breadth-first-search)和深度优先搜索DFS(depth-first-search)[16-18]的排序.在网络可靠性分析领域,文献[19]指出,对于规则网络,BFS策略优于DFS.文献[15,17]指出,对于一般网络,BFS具有较好性能;就BFS排序策略而言,排序起点对排序结果有重大影响.文献[20]指出:1)源点(默认排序起点)一般不是最佳排序起点;2)Square Lattice网络的最佳排序起点分布在4个角上.在考虑节点和边都可能随机失效的情况下,文献[21-22]提出了新的启发式排序策略,在规则网络中的大量实验表明,新的策略优于BFS和DFS.文献[23]针对带社区结构的物联网,提出带权重的BFS和DFS排序.文献[24]结合网络结构特征提出了一种排序策略选择方法,用于构建精简BDD模型.文献[25]重点研究指标数据,用于指导设计排序策略.在模型构建方面,Kuo等[15]提出了基于边扩展图的自底向上的BDD构建方法;Hardy等[17]提出了基于边界集的自顶向下的BDD构建方法.这2种方法适合处理节点完好的网络可靠性分析.在节点和边都可能随机独立失效时,Pan等[26]提出了基于依赖集的模型构建方法;Kawahara 等[27]考虑节点失效时依赖于该节点的边都失效的实际提出了更为高效的BDD构建方法;Yeh等[28]提出二叉加法树(binary addition tree,BAT)算法评估二元状态网络的可靠性.
最近20年,尽管学界在BDD模型构建方法上取得了一些进展,但在启发式排序上鲜有成果.本文考虑节点完好的应用场景,从分析基于边界集的BDD模型构建方法入手,分析影响BDD模型大小的因素,研究排序起点选择方法和启发式排序策略,建立新的启发式排序方法.
1 可靠性网络和BDD模型
1.1 可靠性网络
可靠性网络通常表示为一个无向图G=(V,E,K),其中V是节点集,表示网络系统中的实体;E是边集,表示实体之间的连接;K⊆V是网络中的关键节点(|K|≥2),表示网络中的关键实体,|K|和|V|分别表示关键节点集K和节点集V的大小.所谓网络可靠性,是指K中节点能正常通信(如存在一条连通路径)的可能性.根据集合K大小的不同,将可靠性网络分为3类:2-端可靠性网络(|K|=2)、K-端可靠性网络(2<|K|<|V|)和All-端可靠性网络(|K|=|V|).本文考虑2-端可靠性网络,也称(s,t)网络,其中称s为源点,t为汇点,研究节点s和t之间的连通性.如图1所示,其网络可表示为G=({s,n1,n2,t},{e1,e2,e3,e4,e5},{s,t}).

图1 桥接网络
1.2 BDD模型
在可靠性网络中,网络可靠性问题可以表示为一个等价的布尔函数.BDD是一个有向无环图,通常用来编码布尔函数.基本编码规则如图2所示,其中x为函数f的一个布尔变量,表示网络中的一个部件,fx=0是x=0时的孩子节点(记为左孩子),表示部件失效时的布尔函数,fx=1是x=1时的孩子节点(记为右孩子),表示部件正常工作时的布尔函数.即根据部件失效与否,函数f可以表示为f=p·fx=1+(1-p)·fx=0.其中:p表示部件x正常工作时的概率;fx=0和fx=1仍为布尔函数,可以持续向下分解,直到所有部件考虑完毕,从而得到最终的BDD模型.
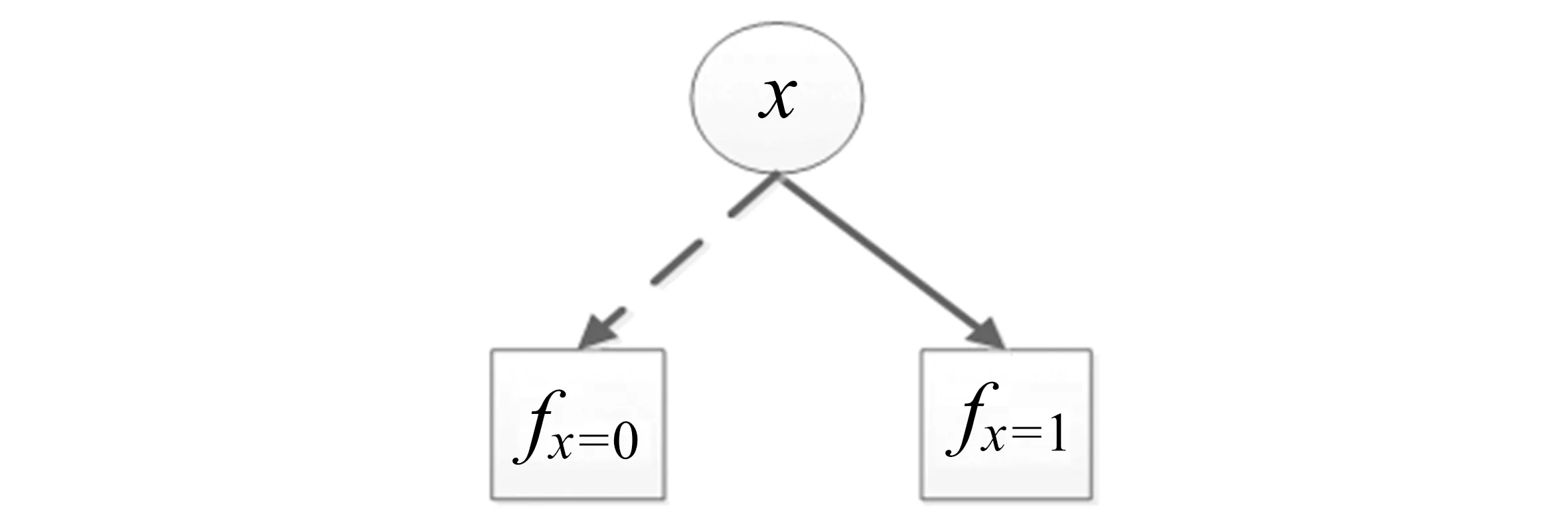
图2 BDD和布尔函数f=p·fx=1+(1-p)·fx=0
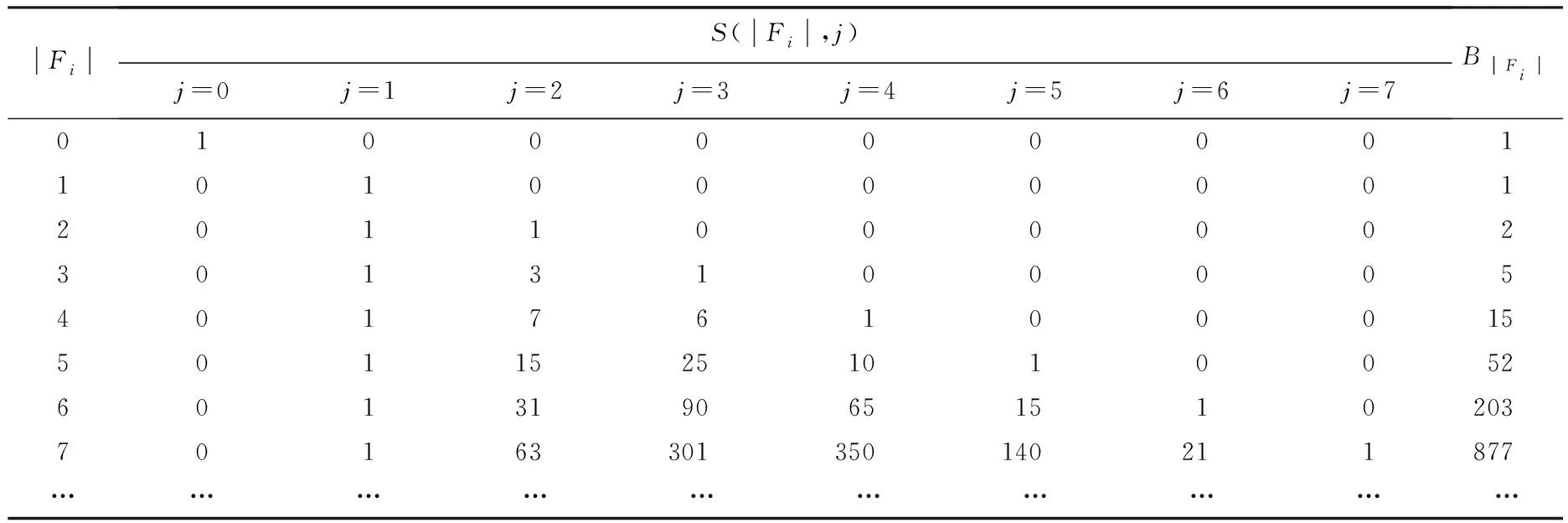
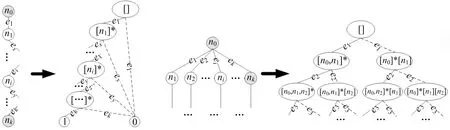
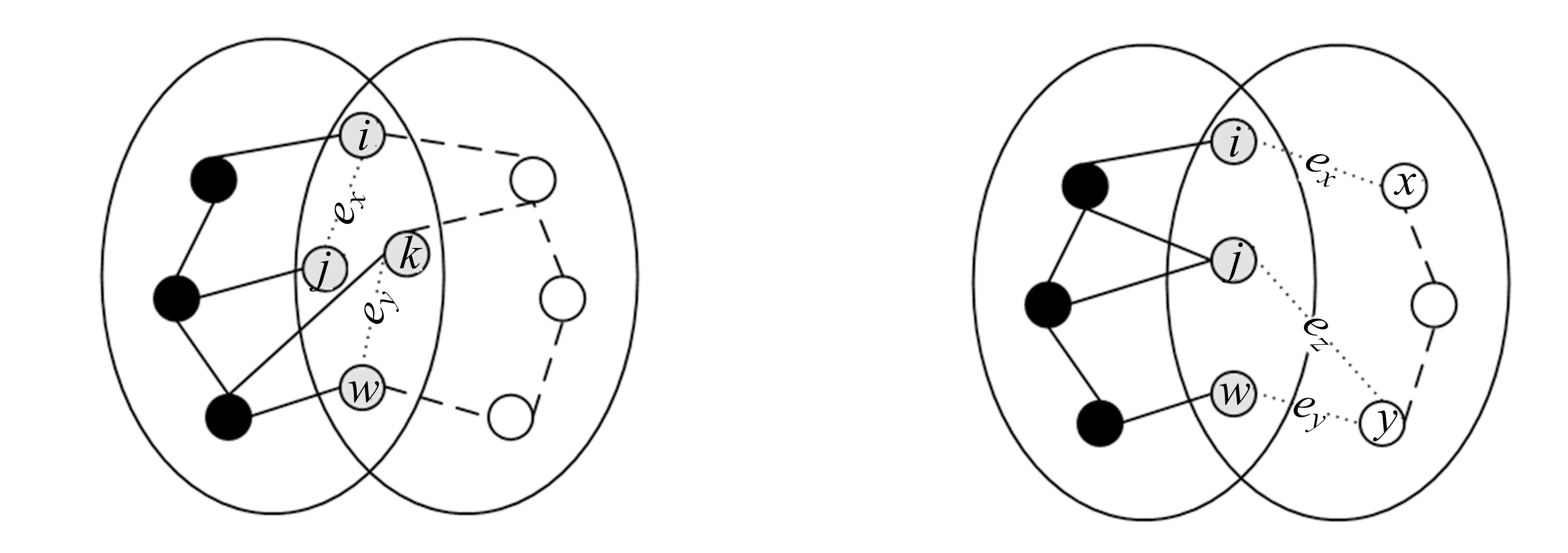
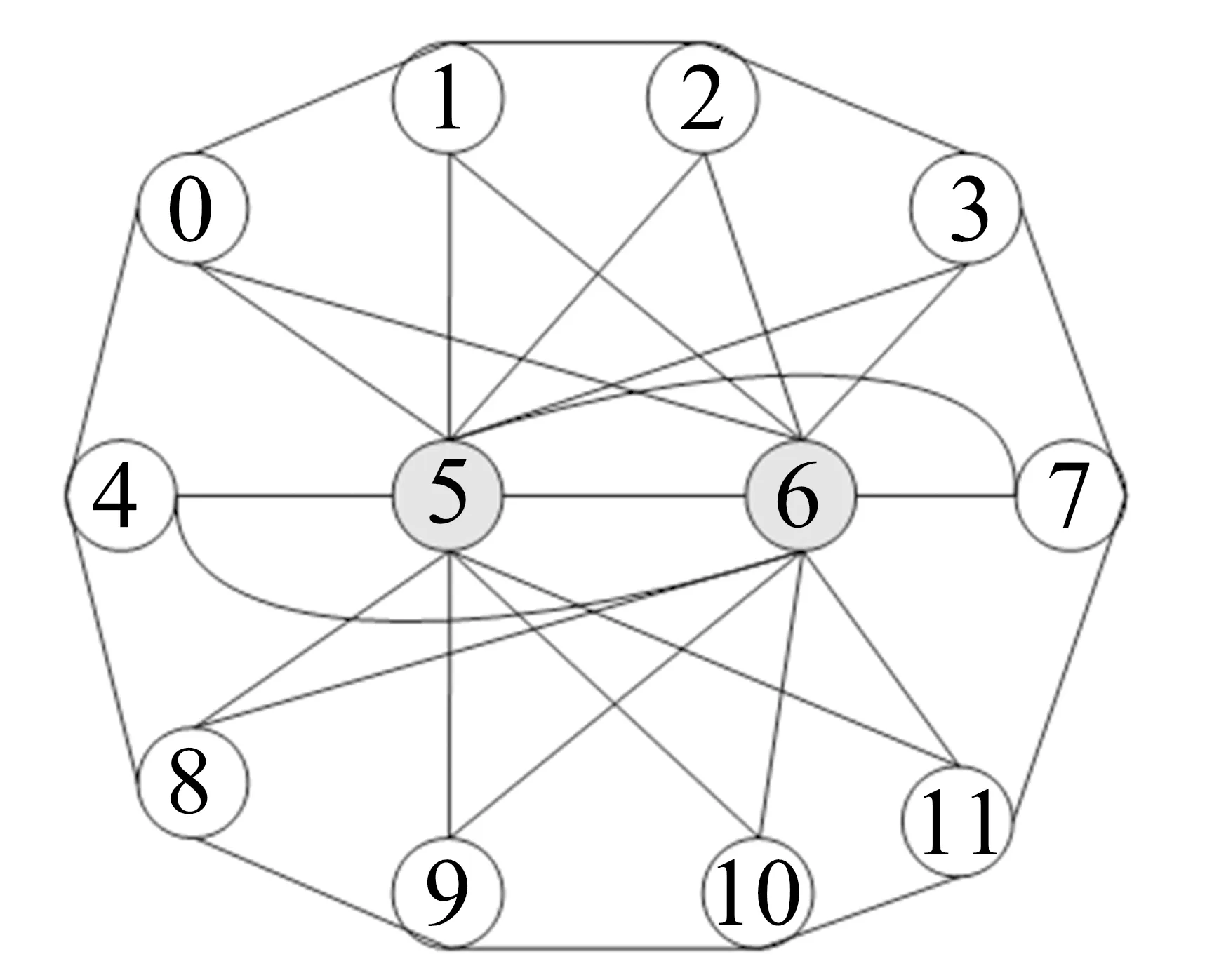
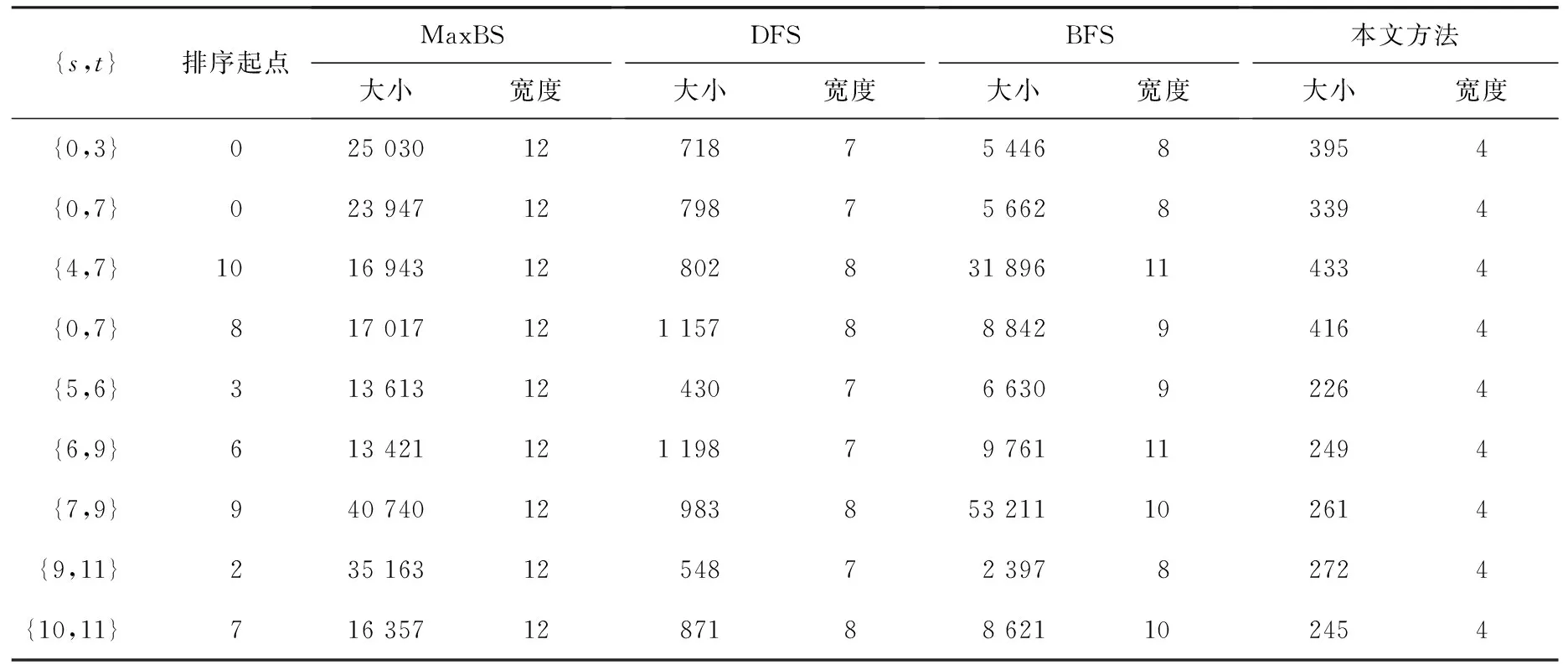
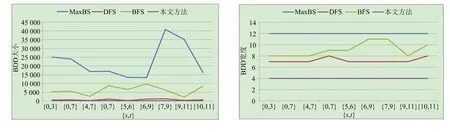
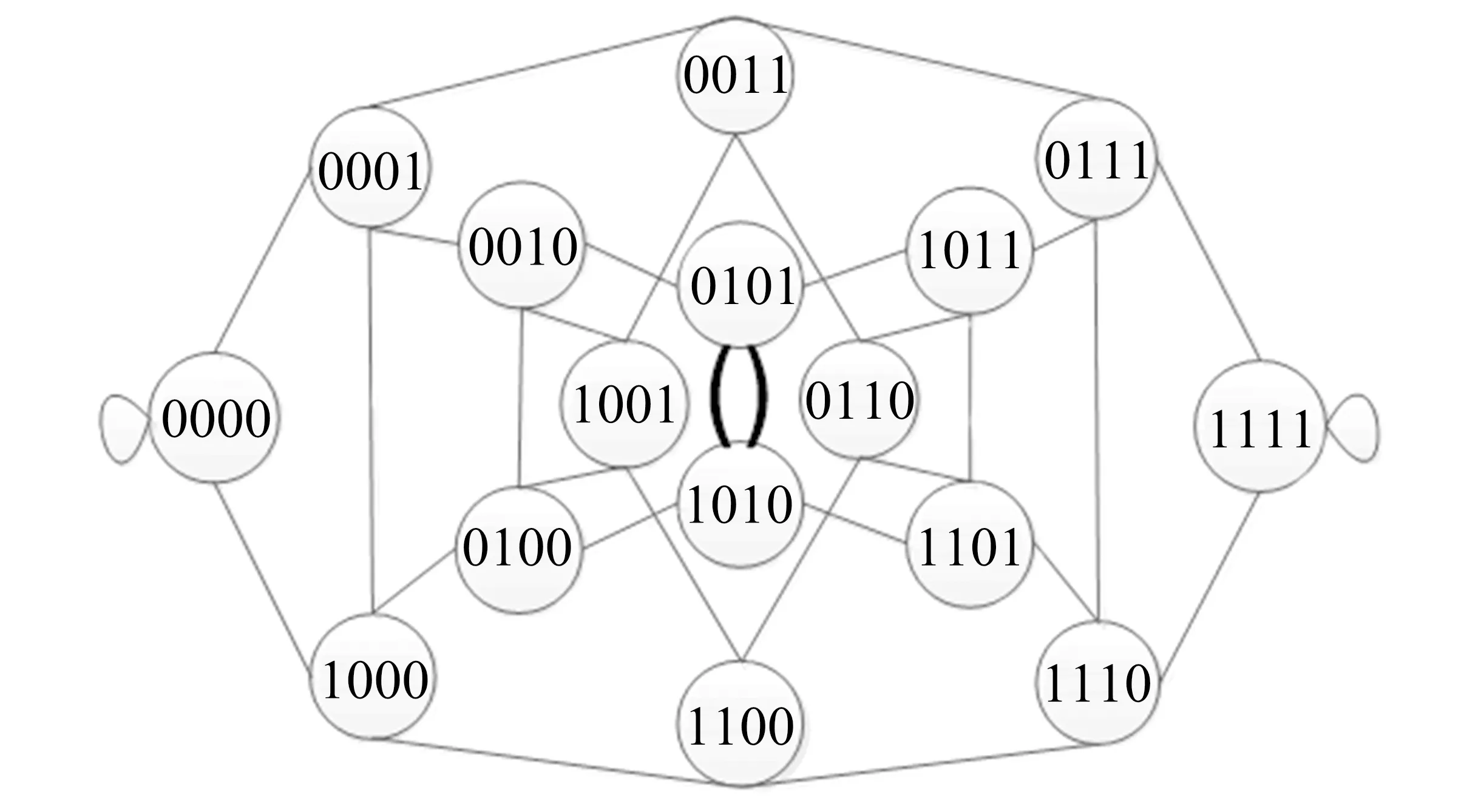
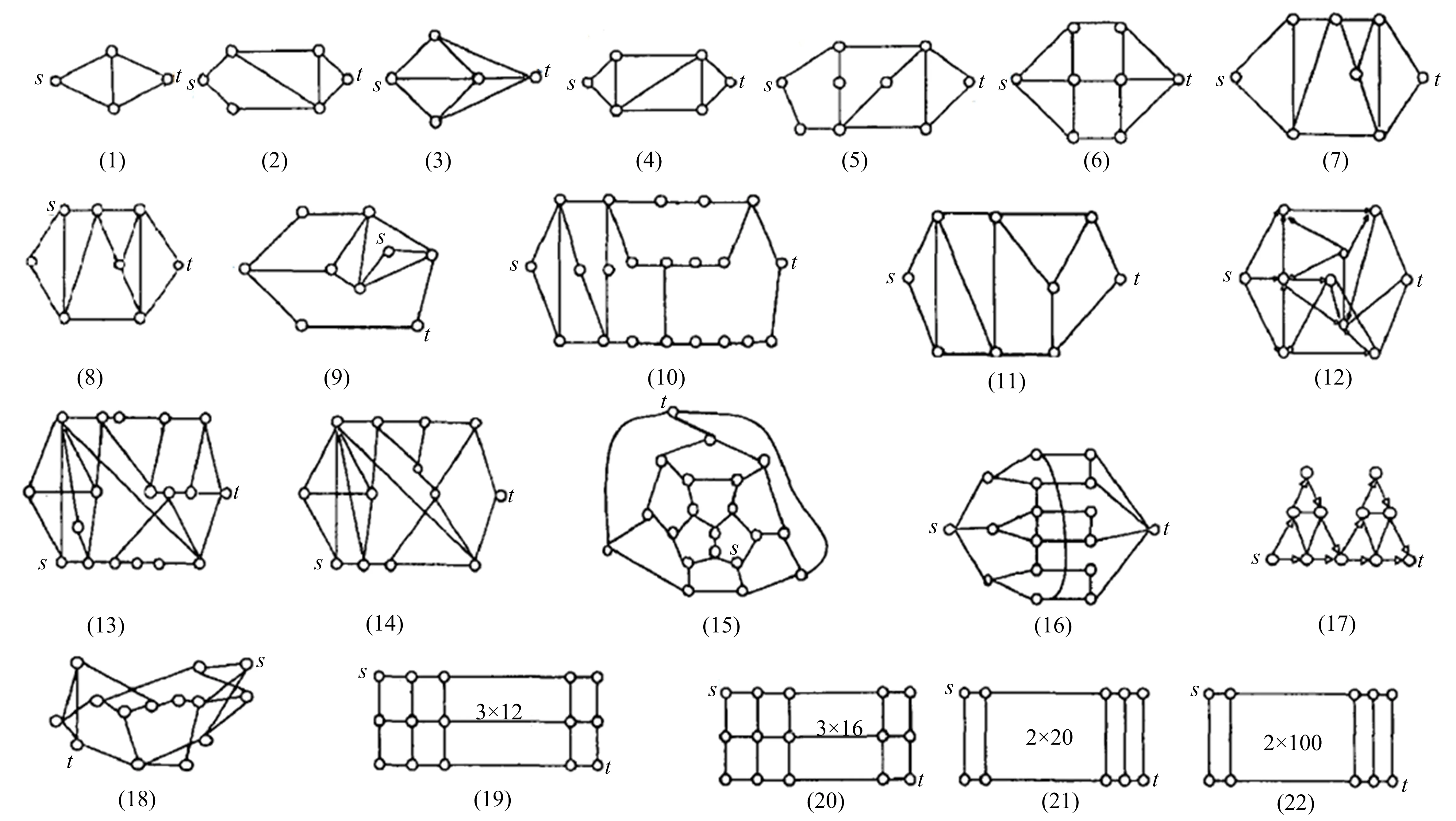
显然,在自顶向下的分解过程中,所考虑部件的出现顺序可以不同.设有布尔函数f=x1x2+x3x4+x5x6,若按部件序x1 (a)低质量排序 (b)高质量排序 定义1(边界集,boundary set) 对于网络G=(V,E,K),假设用边序o=e1≤e2≤…≤e|E|,ei∈E,i∈[1,|E|]来指导生成BDD模型,|E|表示边的数目.当处理第k条边ek时,对应的边界集Fk可定义为 Fk={v|v是ei和ej的一个公共端点,并且ei∈Ek和ej∈E-Ek},Ek={e1,e2,…,ek}. 集合Fi中节点的数目定义为第i层边界集的长度,记Fmax为最大边界集的长度,即 Fmax= max{|Fi|,i= 1,2,3,…,|E|}. 表1 排序o的各层边界集及边界集长度 如图1所示的桥接网络,设有边序o=e1≤e2≤e3≤e4≤e5,则各层边界集及边界集长度如表1所示.因此,最大边界集长度Fmax为2. 定义2(分区,partition) 在用BDD编码网络时,需要建立分区[15]来标记网络特征.分区由若干块构成,块由边界集中的节点构成.具体构建规则如下: 1)若边界集中的2个节点vi和vj通过已经处理的边能够连接在一起,则它们在同一块中,记为[vi,vj],否则处在不同的块中,记为[vi][vj]; 2)若某一块中的节点通过已经处理的边能够和至少1个来自集合K的节点连通,则该块标记为带“*”(称为块加星操作),如[vi,vj]*表示块[vi,vj]与集合K中的某点连通. 分区能有效表征网络[15],如图1所示网络,约定边序o=e1≤e2≤e3≤e4≤e5.显然,考虑边e1时,分区[s,n1]*和[s]*[n1]有效区分了e1正常工作和失效这2种状态,即表征了对应的子网,如图4所示.另外,利用分区标识技术,还可以高效地识别出其中存在的同构,如图4中L2所示,基于分区[n1,n2]*,[n1]*[n2] 和[n1][n2]*,在边e3正常工作时,都得到新的分区[n1,n2]*,识别出了同构,这也符合实际.在同一边序下,分区相同的2个子网同构. 图4 边界集、分区和BDD模型生成过程 引入分区后,可以通过操作分区,在指定边序的约束下,按自上向下方式一层一层构建BDD模型.具体算法如下: 算法1 1)创建BDD模型的根节点分区root,初始化为空 2)初始化哈希表hash,用于记录当前层的所有可能分区,初始化队列preQueue,curQueue用于存放分区 3)preQueue.push(root) 4)fork=1 to |E| do 5) while preQueue do 6)Pk=preQueue.pop() 7)tp=genThenPartition(Pk,ek) 8)ep=genElsePartition(Pk,ek) 9) if所有关键点已在tp的一个块中thenPk.getBDD().then = true 10) else if 有一个关键点被孤立thenPk.getBDD().then = false 11) else 12) iftp不在哈希表hash中 then 13) curQueue.push(tp) 14) hash.put(tp) 15)Pk.getBDD().then=tp.getBDD() 16) if所有关键点已在ep的一个块中thenPk.getBDD().else = true 17) else if 有一个关键点被孤立thenPk.getBDD().else = false 18) else 19) ifep不在哈希表hash中 then 20) curQueue.push(ep) 21) hash.put(ep) 22)Pk.getBDD().else=ep.getBDD() 23) end while 24) preQueue=curQueue; 25) curQueue.clear() 26)end for 27)return root 如图1所示的桥接网络,约定边序为e1 第1层,边为e1=(s,n1),其中“s”为关键点,边界集F1={s,n1}.当边正常工作时,节点“s”和“n1”合并到一个块,得分区[s,n1]*;当边失效时,节点“s”和“n1”分属2个块,得分区[s]*[n1]. 第2层,边为e2=(s,n2),由于关联于节点“s”的边即将全部处理完成,所以边界集F2={n1,n2}.考虑第1层分区[s,n1]*,当边e2正常工作时,得分区[n1,n2]*,失效时,得分区[n1]*[n2];考虑分区[s]*[n1],当边e2正常工作时,得分区[n1][n2]*, 失效时,关键节点“s”被隔离,所以指向false. 第3层,边为e3=(1,n2),边界集F3={n1,n2}.当边正常工作时,基于第2层的各分区都生成了相同的分区[n1,n2]*,所以共享之;当边失效时,分别指向各自的分区[n1,n2]*,[n1]*[n2]和[n1][n2]*. 利用相同的规则,计算边界集,生成分区,得到完成的BDD模型. 分区有效表征了网络状态,如图4所示,每个网络代表一个BDD节点.因此,计算出分区的数目,也就得到了BDD模型的大小.首先从边界集入手,讨论边界集大小与分区数目的关系.根据定义2,在给定第i层边界集Fi和不考虑块加“*”操作的前提下,包含j个块的分区数目是一个第二类斯特林数S(|Fi|,j),而包含任意块数的分区总数是一个贝尔数B|Fi|.表2列举了边界集大小和贝尔数之间的关系. (1) (2) 表2 边界集大小、斯特林数和贝尔数之间的关系 显然,随着边界集的增大,贝尔数急剧增大,且速率远大于成倍增长速率.若能控制住边界集大小,就能有效控制住贝尔数. 定义3(BDD宽度W) 设用Wi表示第i层BDD节点数目的最大理论值,则BDD模型的宽度W定义为 (3) 考虑块加“*”操作.在可靠性网络G=(V,E,K)中,由于最多有|K|个关键节点,所以分区中最多包含|K|个带“*”块.关键节点单独成块时,取得最大值|K|.此时,第i层边界集Fi所对应的分区数目,即第i层BDD节点数目的最大理论值Wi可以按式(4)计算. (4) 例如,边界集F={1,2,3}且|K|=2时的所有可能分区:[1,2,3],[1,2,3]*,[1,2][3],[1,2]*[3],[1,2][3]*,[1,2]*[3]*,[1,3][2],[1,3]*[2],[1,3][2]*,[1,3]*[2]*,[1][2,3],[1]*[2,3],[1][2,3]*,[1]*[2,3]*,[1][2][3],[1]*[2][3],[1][2]*[3],[1][2][3]*,[1]*[2]*[3],[1]*[2][3]*,[1][2]*[3]*,[1]*[2]*[3]*. 显然,引入加“*”操作后,分区总数目大大增加. 比较式(2)和式(4),引入带“*”操作后,随着边界集的增大,BDD节点数目的最大理论值以更大的速率快速增长.从最大理论值角度看,在排序过程中,越晚引入关键节点到边界集就越有利于控制最大理论值. 另一方面,深入研究本文所述BDD模型的生成过程,发现某一层实际BDD节点数目的实际值和已经处理的边数及网络结构特征有关.最好情况,第i层BDD节点数为1;最坏情况,第i层BDD节点数为2i,如图5所示.由于同构子网的存在及网络结构特征的差异,一般情况下,第i层BDD节点数目的实际值大于1而小于2i,如图4所示.所以,如果能找到一种排序,使得每层边界集足够小,从而使得BDD节点数目最大理论值大大小于该层BDD数目的最坏情况,那么此排序将会是一种优秀的排序. (a)最好情况 (b)最坏情况 基于边界集的启发式排序采用贪心策略,在排序过程中尽可能优先选择使边界集足够小的边. 根据本文的BDD模型构建方法,第k层分区以第k-1层分区为基础,结合第k条边ek在网络中的连接情况而建立,即由Fk-1构建Fk.为表述方便,设边ek的2个端点分别为u和v,根据u和v在Fk-1和Fk的存在性得边界集大小变化的所有情况,见表3. 表3 边界集大小变化 由表3所示,新的边界集Fk,其大小满足式(5),且不失一般性.所以,在设计边选择策略时,可以优先考虑2个端点都在当前边界集中的边,然后考虑有一个端点不在边界集中的边,这样才能使当前边界集最小.2个端点都不在边界集的情形不用考虑,因为该情形下不可能得到最小的边界集. |Fk-1|-2≤|Fk|≤|Fk-1|+2. (5) 策略1优先选择2个端点u和v都在边界集中的边.若存在多条满足条件的边,则选择节点度和小的边.若节点度和也相同,则先选择与先进入边界集的节点相关联的边.如图6所示,候选边ex和ey,由于边ex的节点度和小于边ey,所以边ex先排. 策略2选择一个端点u在边界集中的边,且该端点度最小,另一端点v有更多的边关联于当前边界集.否则,选择边e=(u,v),u在边界集中,v有最小的度.如图7所示,节点i和w的度最小,但节点y有2条边关联于边界集,所以边ey先排.之后节点y加入新的边界集,边ez的选择适用策略1. 图6 策略1示意图 图7 策略2示意图 关键节点的引入时机也是一个重要影响因素,所以当候选边关联于关键节点时,该边延迟排序. 基于边界集的启发式排序,其最终排序结果除了和排序策略相关外,还与排序的初始条件有关. 定义4(边界集总长度) 对于给定K-端网络G=(V,E,K),设有一个边序列o=e1≤e2≤e3≤…≤e|E|,ci∈E,i∈[1,|E|],则关于序列o的边界集总长度(记为LTBS(o))定义为 其中,|Fi|为序列o的第i层边界集长度.在确定排序起点之前,先计算不同排序起点的边界集总长度LTBS(O(vi)),其中O(vi)表示以vi为排序起点的一种排序结果,选取边界集总长度值最小的那个节点作为排序起点.NS(V)表示在节点集V中取排序起点. NS(V)=vi⟺LTBS(O(vi))=min{LTBS(O(vi)),vi∈V}. 基于边界集的启发式排序主要包含2个部分:1)排序起点选择;2)排序过程推进.在过程推进中,采用贪心策略,确保每层生成的边界集长度尽可能小.具体算法如下: 算法2 1)选择一个节点v∈V,节点v拥有最小的边界集总长度 2)初始化边界集F0={v} 3)whileFk≠Ø do //策略1: 4) for alle(u,v)∈E-Ek,u,v∈Fkdo 5) order.add(e),G.delete(e),update(Fk) 6) end for //策略2: 7) 选择一点u∈Fk且u的度最小,在u的邻接点中选择一点v,且v拥有最多的未排序边关联于Fk 8) order.add(e(u,v)),G.delete(e(u,v)),update(Fk) 9) 选择一点u∈Fk且deg(u)最小,在u的邻接点中选择一点v,且v的度最小 10) order.add(e(u,v)),G.delete(e(u,v)),update(Fk) 11) end while 12) return order 选择星型网络和De-Bruijn网络分别验证本文提出的启发式排序策略和排序起点选择方法,搜集相关文献的样本网络,用来比较常用启发式排序的性能,并在工程实际网络中进一步验证本文提出的启发式排序方法. Star网络(见图8)中的节点(除去中心节点)具有相似的结构特征,可以最大限度地降低对排序策略的影响.为了更好地说明排序策略,建立了4类排序:1)以快速最大化边界集(MaxBS)的方式建立边排序,即优先选择节点不在边界集中的边进行排序;2)以深度优先搜索(DFS)方式建立边排序,理论上边界集长度每次增1,直到所有节点都加入边界集;3)以广度优先搜索方式(BFS)建立边排序;4)以最小化边界集方式(本文方法)建立边排序. 图8 Star网络 实验步骤如下,实验结果如表4所示. 1)随机选择一个排序起点,根据4种不同排序策略建立边排序; 2)随机选择节点对,建立BDD模型,计算BDD模型大小和BDD宽度. 表4 Star网络的BDD模型大小和宽度 4种排序中,MaxBS的排序结果与排序起点无关,其余3种与排序起点的选择有关.在相同的排序策略下,可以建立不同的排序结果,而不同的排序结果指导生成不同大小的BDD模型,如表4,即使求解相同的问题(计算节点对{0,7}的可靠度),也能生成不同大小的BDD模型.比较BDD模型宽度和模型大小的关系,所得结果见图9.由图9可得,对于不同的排序策略,当BDD模型宽度较小时,对应的模型大小也较小;反之,当模型宽度较大时,模型大小较大.控制BDD模型宽度,有利于控制BDD模型大小. (a)模型大小 (b)模型宽度 在De-Bruijn网络(见图10)中,不同排序起点有不同的边界集总长度.采用本文提出的启发式排序策略时,各排序起点对应的边界集总长度如表5所示,节点“0”“1”和“8”拥有最小的边界集总长度. 图10 De-Bruijn网络(Order=4) 表5 各排序起点的边界集总长度 以下实验说明选择排序起点的必要性,实验过程如下,实验数据如表6、表7所示. 表6 BDD模型大小位序分布 表7 边界集总长度大小位序分布 1)采用本文启发式排序策略,根据不同排序起点建立不同的边排序(共16种); 2)根据16种排序分别为每个节点对(共120对)生成等价的BDD模型; 3)选择拥有最小边界集总长度的节点作为起点时,统计对应的BDD模型大小位序的分布; 4)选定最小BDD模型时,统计边界集总长度大小的分布. 由表6和表7看出:当选择拥有最小边界集总长度的节点作为排序起点时,最小BDD模型占18.6%,前4小BDD模型占比高达91.7%.对应地,当取最小BDD模型时,最小边界集总长度占55.8%,前4小BDD模型占88.3%.由此可得,选择拥有最小边界集总长度的节点作为排序起点时,可以大概率提升排序质量,从而指导生成更小的BDD模型. 本文在相关文献中搜集了22个2-端可靠性网络,如图11所示,采用基于边界集的BDD构建方法,结合本文提出的启发式排序,生成等价BDD模型,计算可靠度值和模型大小,实验结果如表8所示,其中DFS和BFS的数据来自文献[15],“*”表示原BDD构建方法无法生成BDD模型. 图11 样本网络 表8 DFS,BFS和本文方法性能比较 表8数据表明,BFS略优于DFS,而本文提出的启发式排序全面优于BFS和DFS. BDD模型大小严重影响基于BDD的网络可靠性分析方法性能,而BDD模型大小由所采用的变量大小决定,所以寻找优质排序是所有基于BDD分析方法的核心问题.本文从研究基于边界集的BDD构建方法入手,深入分析各层BDD节点的产生过程,总结启发式数据:BDD宽度和边界集总长度,提出排序起点选择方法和尽可能确保BDD宽度小的排序策略.大量实验表明,本文提出的启发式排序方法优于BFS,具有很好的应用价值.在今后的工作中,将进一步研究关键节点和网络结构特征对排序质量的影响,寻找更为优秀的启发式排序.
2 基于边界集的BDD模型构建方法
2.1 边界集和分区

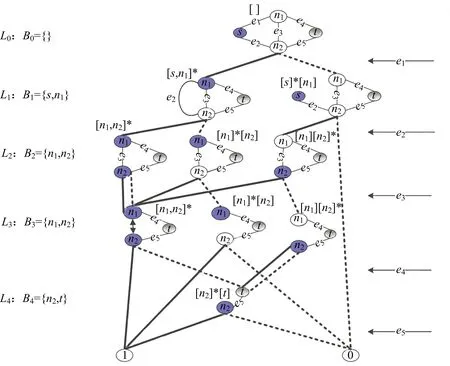
2.2 BDD模型构建
2.3 BDD模型大小分析
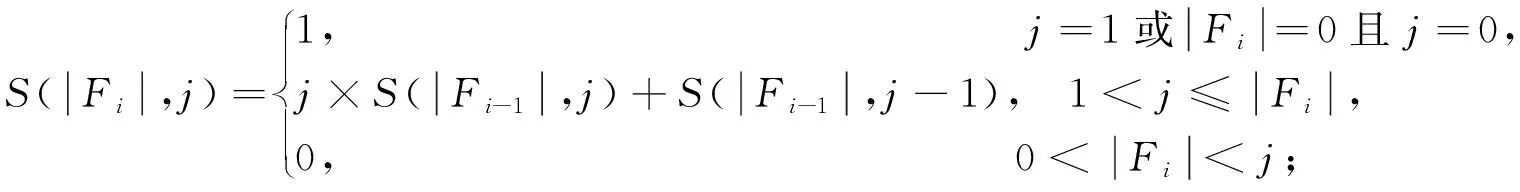
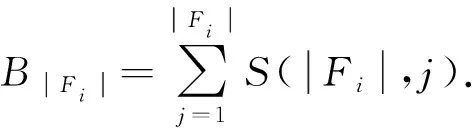


3 基于边界集的启发式排序策略
3.1 排序策略设计

3.2 排序起点选择
3.3 基于边界集的启发式排序算法
4 实验和结论
4.1 Star网络
4.2 De-Bruijn网络


4.3 样本网络

5 结 语

