3维不可压Boussinesq方程在BMO-1空间和各向异性Lorentz空间中的正则性准则
周 沙, 罗虎啸
(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
0 引 言
本文研究如下的 3 维不可压Boussinesq方程组:
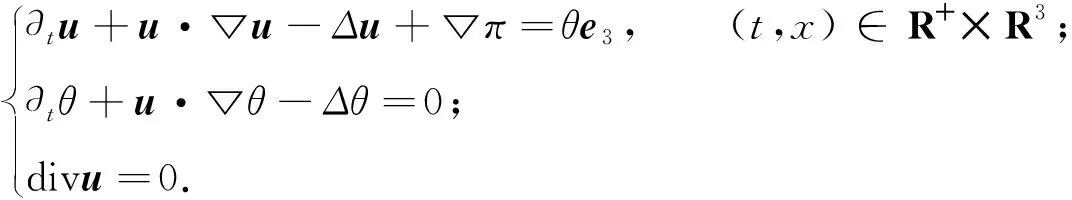
(1)
式(1)中:u=(u1(x,t),u2(x,t),u3(x,t))表示速度;θ=θ(x,t)表示温度;π=π(x,t)表示压力;u0和θ0表示初始速度和初始温度,且在分布意义下▽·u0=0;e3=(0,0,1).Boussinesq方程组是流体力学中一类非常重要的数学模型,它是速度场与温度场耦合而形成的方程,描述了一种热力对流现象.该方程组在大气科学、地球物理科学和海洋环流中有着广泛应用[1].
当θ=0时,方程组(1)退化为经典的3维Navier-Stokes方程组.Navier-Stokes方程组光滑解的全局存在性和唯一性一直以来是一个公开问题.因此,许多学者给出了解的正则性准则.例如,文献[2-3]证明:若u满足经典的Serrin型准则
则解u是正则的.更多关于正则性的结果见文献[4-6].

(2)
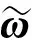
对于3维Boussinesq方程组(1),Ishimura等[8]获得了第1个爆破准则,即
▽u∈L1(0,T;L∞(R3)).
则解(u,θ)在[0,T]上是正则的.文献[12]证明:若▽u满足条件
则解(u,θ)在[0,T]上是正则的.
本文的结果如下:
定理1假定(u,θ)是方程组(1)的一个光滑解,初值(u0,θ0)∈H3(R3).若进一步假定ω=▽×u满足
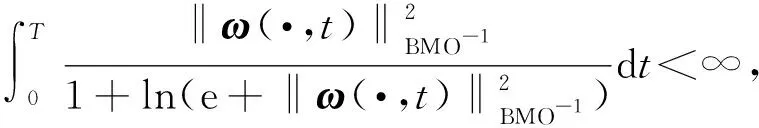
(3)
则解(u,θ)在[0,T]上是正则的,即 (u,θ)∈C([0,T];H3(R3)).
注1条件(3)可看作如下正则性条件的对数型改进:
注2文献[7]考虑的是涡度的2个分量在BMO-1空间中的正则性准则,而本文考虑的是涡度在BMO-1空间中的对数型正则性准则.从形式上看,本文的结果与文献[7]的结果不同.若把文献[7]中初值u0的正则性提高到H3,则条件(2)也可以改成相应的对数型准则.
近几年来,许多学者就Boussinesq方程组(1)关于压力π的正则性问题进行了研究.例如,文献[13-14]得到了在不同的Besov空间中π的正则性准则.最近,文献[15]证明:若π满足
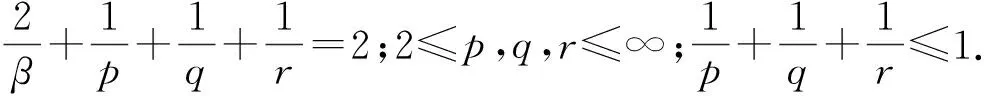
受上述工作的启发,本文借助于各向异性Lorentz空间中的一些不等式,将文献[15]的结果推广到各向异性Lorentz空间.其中关于各向异性Lorentz空间见下文定义5.
定理2假定(u,θ)是方程组(1)的一个弱解,初值(u0,θ0)∈H1(R3)∩L4(R3).若进一步假定π满足

(4)

1 基本概念
为方便起见,先来回顾一下3维Boussinesq方程组(1)的弱解定义.
定义1若定义在R3×(0,T)的函数(u,θ)满足如下条件,则称(u,θ)是方程组(1)的弱解:
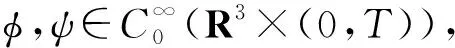
定义2[16]BMO空间由局部可积函数f组成,使得
这里是对R3中所有的球B取上确界.
在BMO空间的基础上,给出 BMO-1空间的定义.
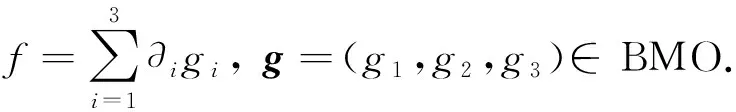
其范数定义为
下面回忆Lorentz空间和各向异性Lorentz空间的基本定义.
设(X,M,ν)是非原子测度空间.对一个定义在X上的实值或复值的ν测度函数f,它的分布函数定义为
df(σ)=ν{x∈X:|f(x)|>σ},σ>0,
f*(t)=inf{σ:df(σ)≤t}(t>0)是f的递减重排.
定义4[17]设(p,q)∈[1,∞]2,Lorentz空间Lp,q(X,M,ν)是由‖f‖Lp,q<∞的所有定义在X上的实值或复值的ν测度函数f组成的集合.其中:
设f=f(x1,x2,x3)是一个定义在R3的可测函数,f*(t)=f*1,*2,*3(t1,t2,t3).其中f*1,*2,*3(t1,t2,t3)是f(x1,x2,x3)的多元递减重排.
定义5[18]设多重指标p=(p1,p2,p3),q=(q1,q2,q3).pi和qi满足:若0 的所有可测函数f的集合. 下面介绍在定理1证明过程中要用到的重要的引理. ‖Λs(fg)-fΛsg‖Lp≤C(‖▽f‖Lp1‖Λs-1g‖Lp2+‖Λsf‖Lp3‖g‖Lp4). 接下来给出在各向异性Lorentz空间中的Hölder不等式和相关的范数估计. 引理3[20]设1≤p1,p2,q1,q2≤∞,则对于任意的f∈Lp1,q1(Rn),g∈Lp2,q2(Rn),有 ‖fg‖Lp,q≤C‖f‖Lp1,q1‖g‖Lp2,q2. 定理1的证明根据解的局部存在理论,对于初值为(u0,θ0)∈H3(R3)的方程组(1)在[0,T)上存在唯一解,T>0.因此,为了证明定理1,只需证明 (5) 首先,给出方程组(1)基本的能量估计.为了叙述方便,将方程组(1)中的第1个方程记为(1)1、方程组(1)中的第2个方程记为(1)2.方程(1)1和(1)2两边分别与u,θ作内积可得 由Gronwall不等式得 接下来估计ω=▽×u及▽θ.方程(1)1两边取旋度,所得方程两边与ω作L2内积;同样地,方程 (1)2两边与Δθ作L2内积.把2个式子相加后可以得到 对于I1,根据引理1和Young不等式,有 I1≤C‖ω‖BMO-1(‖▽(▽u)‖L2‖ω‖L2+‖▽u‖L2‖▽ω‖L2)≤ (6) 对于I3,用相同的方法得到 I3≤C‖▽u‖BMO-1‖▽θ‖L2‖Δθ‖L2≤ (7) 对于I2,运用Hölder不等式和Young不等式,有 (8) 因此,结合式(6)~式(8),有 (9) 这里使用了如下的空间嵌入关系和插值不等式: 由条件(3)可知,对于任意的ε>0,存在T0∈(0,T),使得 记 (10) 则式(9)即为 (11) 对式(11)在[T0,t]上运用Gronwall不等式,有 C0exp(2Cεln(e+X(t)))≤C0(e+X(t))2Cε. (12) 式(12)中,C0是依赖于T0的常数. 下面对‖u‖H3进行估计.在方程(1)1两边同时作用Λ3,再与Λ3u作L2内积;同样地,在 (1)2两边同时作用Λ3,再与Λ3θ作L2内积.将2个式子相加,利用divu=0的条件,得到 (13) 对于I11,根据引理 2、Gagliardo-Nirenberg不等式和Young不等式,有 (14) 结合式(12)和式(14),有 对于I13,用同样的方法可得到 I13≤C(‖▽u‖L3‖Λ3θ‖L3+‖▽θ‖L3‖Λ3u‖L3)‖Λ3θ‖L3≤ 对于I12,由Hölder不等式、Young不等式及式(10)得到 把I11,I12和I13的估计代入式(13),得 (15) 定理1证毕. 定理2的证明根据解的局部存在结果可知,以 (u0,θ0)∈H1(R3)∩L4(R3)为初值的方程组(1)在[0,T)上存在唯一解,T>0.因此,为了证明定理2,只需证明 (16) 首先,对方程(1)2两边在R3上积分,利用divu=0的条件,计算出 进一步有 这就得到了θ的L1估计.再对方程(1)2运用最大值估计,得到θ的L∞估计,即 从而有θ的全局先验估计,即 ‖θ(·,t)‖Lp≤‖θ0‖Lp, ∀t∈[0,T], 1≤p≤∞. (17) 运用散度公式和Young不等式,M1可以被估计为 (18) 接下来,为了处理式(18)中不等号右边的第1项,需要估计‖π‖Lp和‖▽π‖Lp,1 -Δπ=∂i∂j(uiuj)-∂3θ,i,j=1,2,3. 因此, -Δ▽π=∂i∂j(ui▽uj+uj▽ui)-∂3▽θ, 从而 ▽π=RiRj(ui▽uj+uj▽ui)-R3Rθ; 其中: 表示 3 维空间下的里斯变换.利用里斯变换在Lp(1 ‖▽π‖Lp≤C(‖|u||▽u|‖Lp+‖θ‖Lp)≤C(‖|u||▽u|‖Lp+‖θ0‖Lp)≤ C(‖|u||▽u|‖Lp+1); 进而,应用引理3、引理4和Young不等式对式(18)中不等号右边第1项进行估计,得 (19) 这里用到下面的不等式: (20) 对于M2,运用Hölder不等式和Young不等式得到 (21) 将式(20)和式(21)代入式(17)得到 (22) 下面使用Young不等式,可计算出 为了简化计算,记 因此,可以将式(22)转化为 进一步有 运用Gronwall不等式,即有 (23) 结合式(4),可以推断出 (24) 定理2证毕. 本文是在前人研究成果的基础上,运用能量方法,得到了3维Boussinesq方程在BMO-1空间和各向异性Lorentz空间下解的2个正则性准则.在本文研究的基础上,将来还可以进一步研究Boussinesq方程在更优的空间下关于速度的某一方向偏导的正则性准则.2 引 理
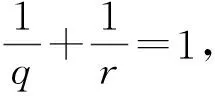
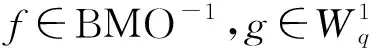


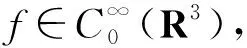
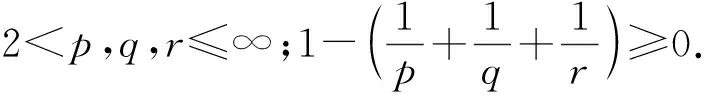
3 定理的证明
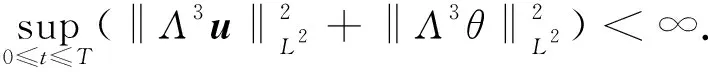
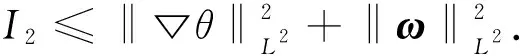



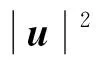
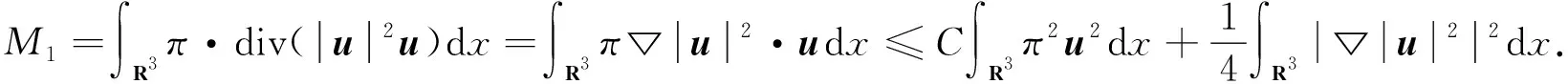
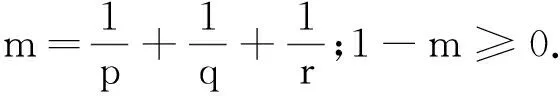
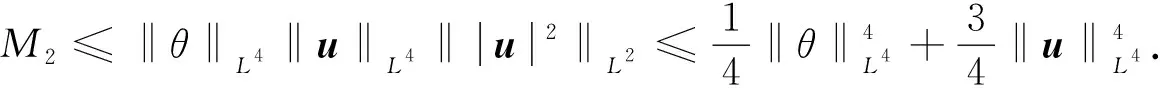


4 结 语

