半无限板边缘裂纹的权函数解法与评价1)

童第华吴学仁胡本润陈勃

(北京航空材料研究院，北京100095)

固体力学

半无限板边缘裂纹的权函数解法与评价1)

童第华吴学仁2)胡本润陈勃

(北京航空材料研究院，北京100095)

权函数法是求解裂纹体在任意受载条件下的应力强度因子和裂纹面位移等断裂力学参量的高效、高精度方法，与有限元等数值方法相比,在求解效率和可靠性方面均具有明显优势.针对半无限板边缘裂纹，系统分析了在国际断裂力学界较有代表性的Wu-Carlsson、Glinka-Shen和Fett-Munz三种解析形式的权函数法，进而以在远端均匀加载下的半无限板边缘裂纹面位移Wigglesworth解析解导得的权函数及其对应的格林函数解(即裂纹面受一对单位集中力作用下的应力强度因子)为基准，沿整个裂纹长度对3种权函数的精度逐点进行比较，并与文献中基于其他方法求得的权函数做了广泛对比，包括Bueckner,Hartranft-Sih以及Wigglesworth利用不同解析方法推导出的高精度的权函数.研究了3种参考载荷(均布/正反向线性分布应力、集中力)及其不同组合，以及裂纹嘴位移的几何条件对权函数精度的影响.结果表明，基于一种参考载荷下的裂纹面张开位移比基于两种参考载荷下的应力强度因子所得到的权函数具有更高的精度，而且后一种方法的精度明显受到所选参考载荷组合的影响；裂纹面位移在裂纹嘴处三阶导数等于零的条件对基于一个参考解的权函数精度的改进效果较小.最后给出了利用各种权函数方法计算得到的4种载荷条件下的应力强度因子，并对结果进行了比较.

半无限板,边缘裂纹,权函数法,格林函数,应力强度因子

引言

承受各种载荷作用下的裂纹应力强度因子(K)计算是断裂力学分析中的关键环节.利用有限元法(FEM)或边界元法(BEM)等数值方法计算各种载荷情况和不同长度裂纹的应力强度因子，则往往要付出大量时间，例如高梯度的应力集中、热应力、残余应力和基于塑性诱发的裂纹闭合问题等.

权函数法[12]是一种求解裂纹在任意载荷条件下的应力强度因子和裂纹面位移等断裂力学参量的高效、高精度方法.自Bueckner[1]和Rice[2]提出权函数法以来，许多学者对其作了深入的研究[313].权函数解法的独特优势在于，把影响裂纹尖端应力强度因子和裂纹面位移的两个因素(载荷和几何)作了变量分离.权函数本身仅包含裂纹的几何特征和载荷/位移边界条件，而与载荷无关.一经确定，权函数就成为一个独立于载荷而仅与裂纹几何特性及边界条件有关的函数，可用来不受限制地求解裂纹在任意载荷条件下的应力强度因子.文献[11-12]系统论述了权函数法，并用它求解了大量裂纹问题.

许多学者提出了确定权函数的不同方法.以半无限板边缘裂纹为例，最具代表性的有3种：一是Wu-Carlsson[4]根据假设的裂纹面张开位移的级数展开式，利用裂纹尖端场的特点、自洽条件、裂纹嘴位移和裂纹面位移在裂纹嘴处二阶导数为零的条件推导权函数；二是Glinka-Shen[8]根据假定的权函数表达式形式，利用两种参考载荷情况下的应力强度因子和裂纹面位移在裂纹嘴处二阶导数为零的条件推导权函数系数；三是Fett-Munz[12]根据解析极限情况、一种参考应力强度因子解和裂纹面位移在裂纹嘴处1～3阶导数都等于零的条件推导权函数.在工程实际应用中，具体方法的选择取决于确定权函数的复杂程度和计算精度.本文系统推导了半无限板边缘裂纹的以上3种权函数，对计算精度进行了深入分析.在此基础上与文献中的结果进行了广泛对比，包括Bueckner[14]、Hartranft-Sih[15]，以及Wigglesworth[16]利用解析手段推导出的高精度的权函数.

Wu-Carlsson权函数法[11]只需要一种参考载荷情况的应力强度因子解和裂纹嘴位移.而Glinka-Shen[8]提出的确定权函数的方法则需要两种参考载荷情况的应力强度因子解.裂纹面均布载荷是最简单的加载形式，一般将其选为第1种参考载荷，而关于第2种参考载荷选取对权函数精度的影响问题，文献中鲜见报道.本文针对半无限板边缘裂纹情况，选择正向线性分布载荷和反向线性分布载荷作为第2种参考载荷，研究其选取对权函数精度的影响.此外还分析了裂纹面位移在裂纹嘴处三阶导数等于零的条件对提高权函数精度的作用.

在上述研究的基础上，选择了4种相对复杂的加载形式(不同次数的幂函数加载和裂纹面受反向线性载荷作用)，利用以上3种权函数法求解其应力强度因子，并对结果进行了比较分析.

1 边缘裂纹问题的各种权函数解法

根据权函数理论，应力强度因子可以根据权函数m(a,x)和无裂纹情况下假想裂纹处的应力分布σs(x)乘积的积分求得

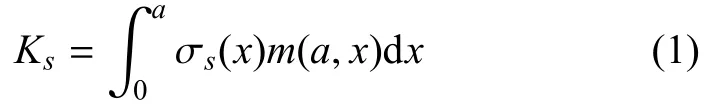
式中,a和x分别是裂纹长度和沿裂纹面的坐标；Ks为载荷情况为s的应力强度因子；σs(x)为载荷情况为s的假想裂纹处的应力分布.式(1)的权函数m(a,x)可以表达为

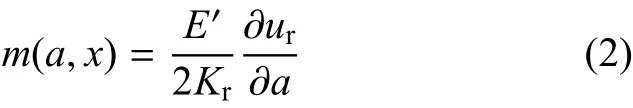
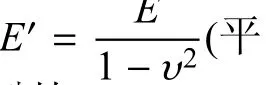
利用式(2)的权函数求解K，首先需要确定不同裂纹几何的裂纹面位移ur与裂纹长度a和坐标x之间的函数关系，而ur很难用解析式表示.下面以半无限板边缘裂纹为例(如图1所示)，讨论较有代表性的3种方法，即Wu-Carlsson[11]、Glinka-Shen[8]和Fett-Munz权函数法[6].

图1 半无限板边缘裂纹Fig.1 An edge crack in a semi-infinit plate

1.1 Wu-Carlsson权函数

对于受多项式分布应力作用下的边缘裂纹，设裂纹面位移的级数展开形式为[11,13]

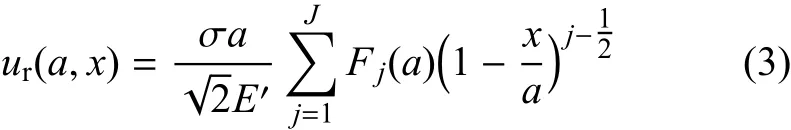
式中,下标r代表参考载荷情况；多项式级数展开的最大项数J取决于可以利用的力学条件数量.对于本文讨论的边缘裂纹问题，所用的4个条件为：(1)裂纹尖端区的裂纹面位移和K的比例关系；(2)自洽条件；(3)裂纹面位移在裂纹嘴处的二阶导数为零；(4)参考载荷作用下裂纹嘴处的位移.上述条件可表达为

条件1

条件2

式中

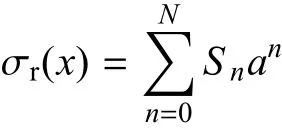
条件3

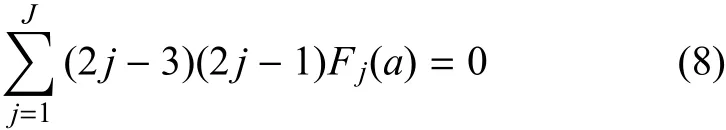
条件4

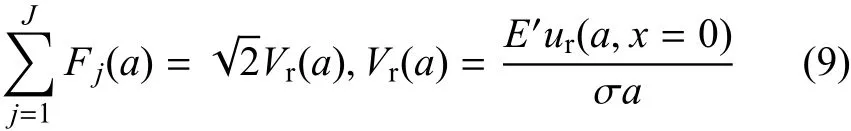
F1(a)～F4(a)的表达式为[11,13]

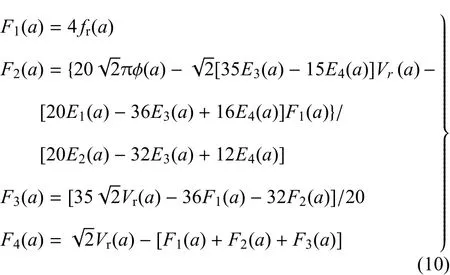
对于半无限板边缘裂纹，选取裂纹面均布应力做为参考载荷(如图2(a)所示)，其无量纲应力强度因子和无量纲裂纹嘴位移的精确解分别为fr=1.1215，Vr=2.9086，且n=0,S0=1,于是简化为Ej=2/(2 j+1).将它们代入式(10)，得到：F1=4.4860，F2=-0.7635，F3=0.3453，F4=0.0456.

图2 半无限板边缘裂纹受不同的载荷作用Fig.2 An edge in a semi-infinit plate subjected to various loading cases

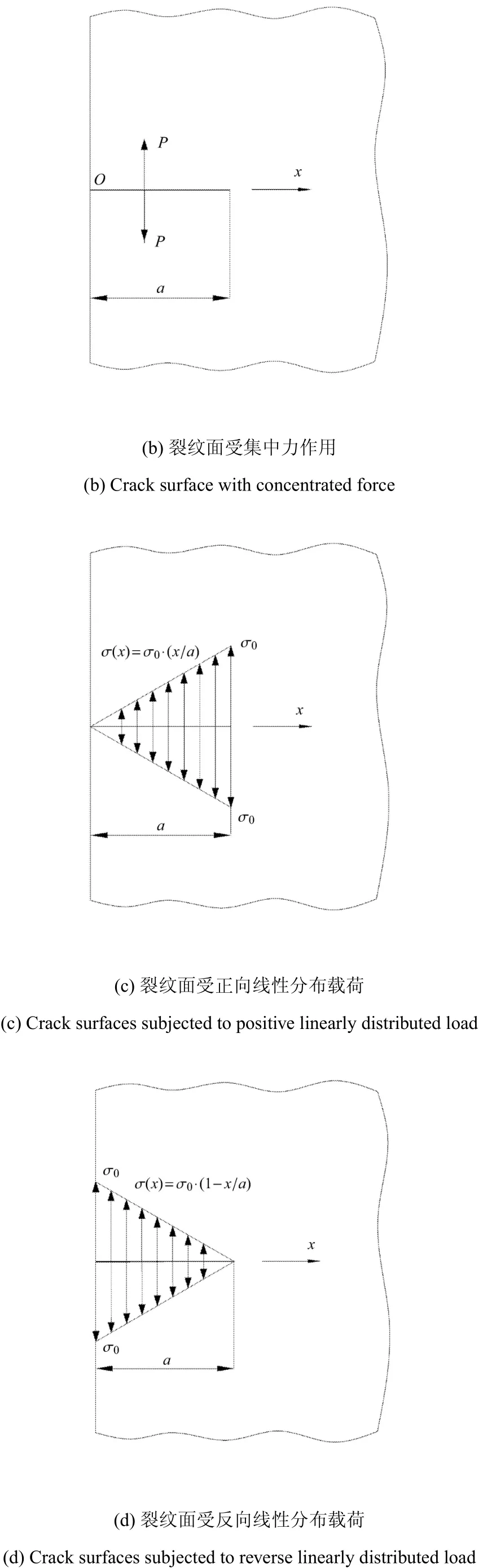
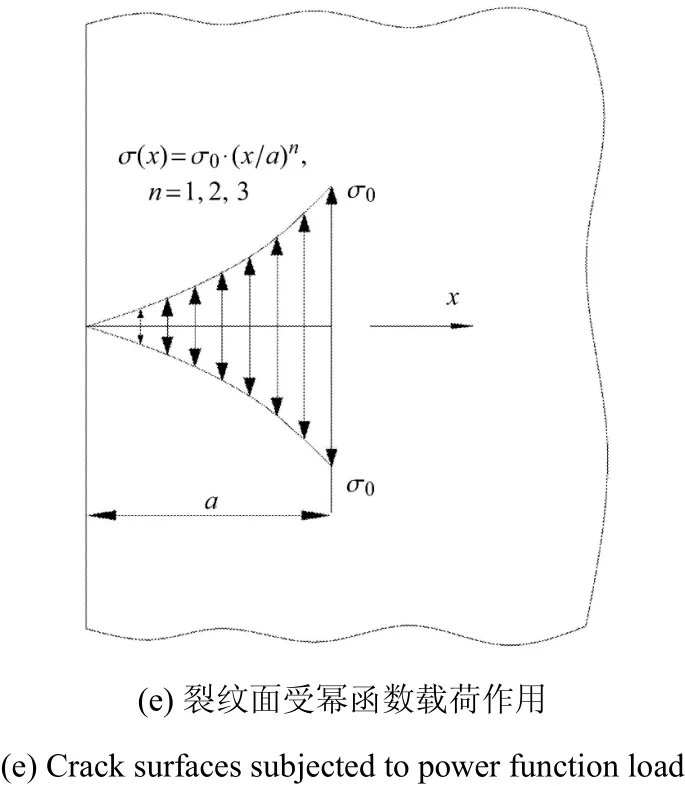
图2 半无限板边缘裂纹受不同的载荷作用Fig.2 An edge in a sem i-infinit plate subjected to various loading cases

将F1～F4代入式(3)，得到半无限板边缘裂纹的裂纹面位移表达式.基于此表达式和式(2)可以直接确定权函数，其结果可以表示为[11,13]

式中

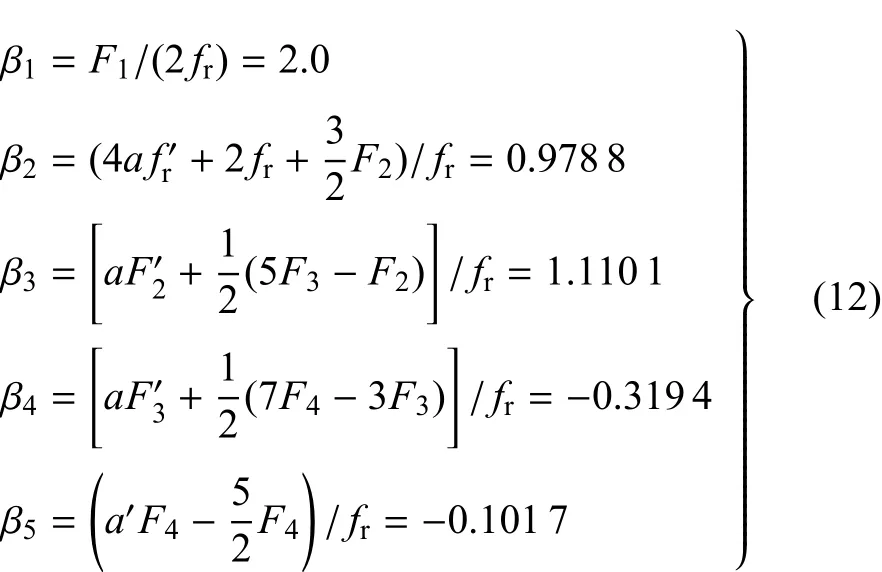
1.2 Glinka-Shen权函数

Glinka-Shen[8]直接假设权函数的一般表达式为

Glinka-Shen[8]认为，对于大部分裂纹几何，式(13)一般取4项即可保证精度.在4项的权函数表达式中有3个待定参数M1,M2和M3.采用3种不同参考应力强度因子或两种不同参考应力强度因子加上边缘裂纹的裂纹面位移在裂纹嘴处二阶导数为零来确定未知参数M1,M2和M3.对于大部分裂纹几何，3种不同参考应力强度因子的获取难度要远大于第2种组合条件，因此大多选用第2种组合条件(见式(14)～式(17))来确定上述3个未知参数.

条件1

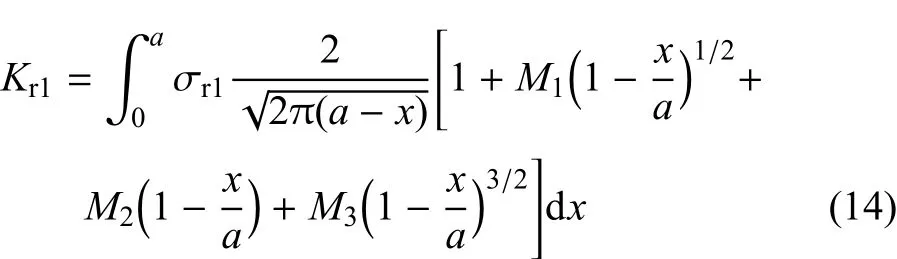
式中,σr1为第一种参考载荷情况下假想裂纹处的应力分布；Kr1为载荷σr1作用下的应力强度因子.

条件2

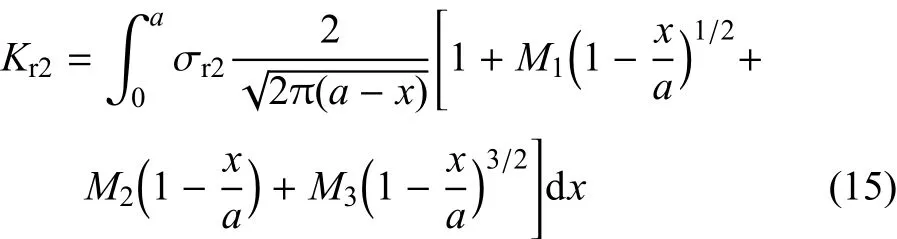
式中,σr2为第二种参考载荷情况下假想裂纹处的应力分布；Kr2为载荷σr2作用下的应力强度因子.

条件3

由于裂纹面位移u(x,a)和权函数m(a,x)存在式(2)的关系，因此条件3也可写为

对于半无限板边缘裂纹，Glinka-Shen[8]选取的第一种参考载荷情况为裂纹面受均布载荷作用(如图2(a)所示)，第2种参考载荷情况为裂纹嘴受集中力作用(如图2(b)所示，x=0)，对应的应力强度因子分别为

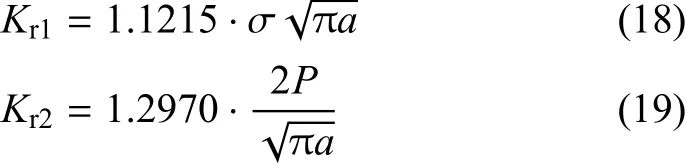
将式(18)和式(19)代入式(14)、式(15)和式(17)可以求得式(13)权函数系数：M1=-0.85154,M2=3.00000和M3=-1.31422.

1.3 Fett-M unz权函数

Fett-Munz[12]假定权函数的一般表达式为

利用以下5个条件确定半无限板边缘裂纹权函数的系数D0～D5.分别为解析极限情况、一种参考应力强度因子解和边缘裂纹的裂纹面位移在裂纹嘴处一阶、二阶和三阶导数都等于零的条件(见式(16)和式(17)的关系)，上述5个条件表示为

条件1

条件2

条件3～条件5

根据上述5个条件，确定了半无限板边缘裂纹权函数的系数[12]D0～D5：D0=0.58852,D1=0.031854,D2=0.463397,D3=0.227211,D4=-0.828528,D5=0.351383.

1.4 权函数精度评价——格林函数法

由以上所确定的权函数计算给定应力分布下的应力强度因子，并与已知的高精度应力强度因子解对比，是评估权函数准确性的一种常用方式.但这种方式实际上并不能准确地评价权函数精度,因为由权函数计算应力强度因子，需要对权函数与无裂纹体假想裂纹面应力分布的乘积沿整个裂纹面做积分.由于积分具有平均效应，所以由积分计算得到的应力强度因子，并不能真实体现权函数本身的准确性.一般而言，当应力分布不发生符号改变时，由于平均效应，应力强度因子的结果误差将小于权函数的最大误差，而当应力分布沿裂纹面有剧烈变化，甚至多次改变应力方向时，应力强度因子的结果误差可能会显著地大于权函数最大误差，有些情况甚至会有数量级的差别.所以，评价权函数本身精度的最佳方法是对权函数沿裂纹面逐点进行比较[11]，即比较格林函数.这种比较方式不会引入任何误差.

格林函数G(a,x)又被称为影响函数，它代表裂纹面在任意位置x受一对单位集中力作用时(图2(b))的无量纲应力强度因子(式(24)).格林函数与裂纹面受一对单位集中力作用下的应力强度因子是逐点对应的，与权函数m(a,x)的关系见式(25).本文采用格林函数评价各种权函数法结果的准确性.

2 半无限板边缘裂纹格林函数解

除上述3种最为常见的权函数解法外，其他学者也用不同的方法给出了半无限板边缘裂纹的格林函数解，例如Bueckner[14](见式(26))和Hartranft-Sih[15](见式(27))(Tada手册[17]中采用的格林函数公式).为了对比上述5种半无限板边缘裂纹格林函数解的精度，以Wigglesworth[16]的半无限板边缘裂纹在远端均匀加载下的高精度裂纹面位移解析表达式推导出的格林函数解做为基础(见式(28))进行比较，结果见图3.

式中

式(29)中,C0～C12分别为

图3表明，以Wigglesworth格林函数[16]为基准，各种格林函数最大相对差别分别如下：Bueckner[14]为1.57%,Wu-Carlsson[11]为0.56%,Fett-Munz[12]为0.23%,Hartranft-Sih[15]为0.78%,Glinka-Shen[8]为8.21%.

图3 半无限板边缘裂纹不同权函数方法求得的格林函数Fig.3 Green’s functions foran edge crack in a sem i-infinit plate derived from di ff erentweight functionmethods

3 参考载荷的选取对G linka-Shen权函数法和Wu-Carlsson权函数法的影响

Glinka-Shen的通用权函数法[8]需要两种参考载荷情况的应力强度因子解作为已知条件来推导权函数，而Wu-Carlsson权函数法[11]只需要一种参考载荷情况的应力强度因子解和裂纹嘴位移.裂纹面受均布应力作用(如图2(a)所示)作为最简单的载荷情况被Glinka-Shen[8]和Wu-Carlsson[11]选用为一种参考载荷情况.Glinka-Shen[8]选用的另一种载荷情况是裂纹嘴受集中力作用(如图2(b)所示，x=0).为了考察文献[8]的方法中参考载荷的选取对权函数精度的影响，本文选取以下3种参考载荷情况的组合来分析参考载荷的选取对权函数精度的影响，分别为：(1)裂纹面受均布应力作用和裂纹嘴受集中力作用(见1.2节)；(2)裂纹面受均布应力和正向线性变化的载荷(如图2(a)和图2(c)所示)；(3)裂纹面受均布应力和反向线性变化的载荷(如图2(a)和图2(d)所示).对于Wu-Carlsson权函数法[11]，分别选取了裂纹面受均布应力(如图2(a)所示)、正向线性变化(如图2(c)所示)和反向线性变化(如图2(d)所示)作为参考载荷情况.

对于裂纹面受正向线性变化载荷(如图2(c)所示)，其应力强度因子和裂纹嘴位移[17]为

对于裂纹面受反向线性变化载荷(如图2(d)所示)，其应力强度因子和裂纹嘴位移[17]为

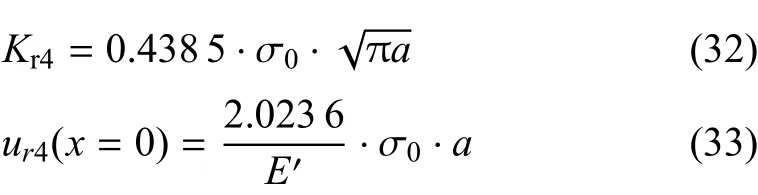
基于Glinka-Shen权函数法[8]，将式(18)和式(30)代入式(14)和式(15)中，求得参考载荷为均布载荷和正向线性变化载荷情况下权函数式(13)的系数为M1=-0.67923,M2=3.0000和M3=-1.65885.将式(18)和式(32)代入式(14)和式(15)中，可以求出参考载荷为均布载荷和反向线性变化载荷情况下权函数式(13)系数为M1=-0.67924,M2=3.0000和M3=-1.65874,其相应的格林函数如图4(a)所示.1.2节中参考载荷为均布载荷和裂纹嘴集中力情况下的格林函数也在图4(a)中给出(M1=-0.85154,M2=3.00000和M3=-1.31422).

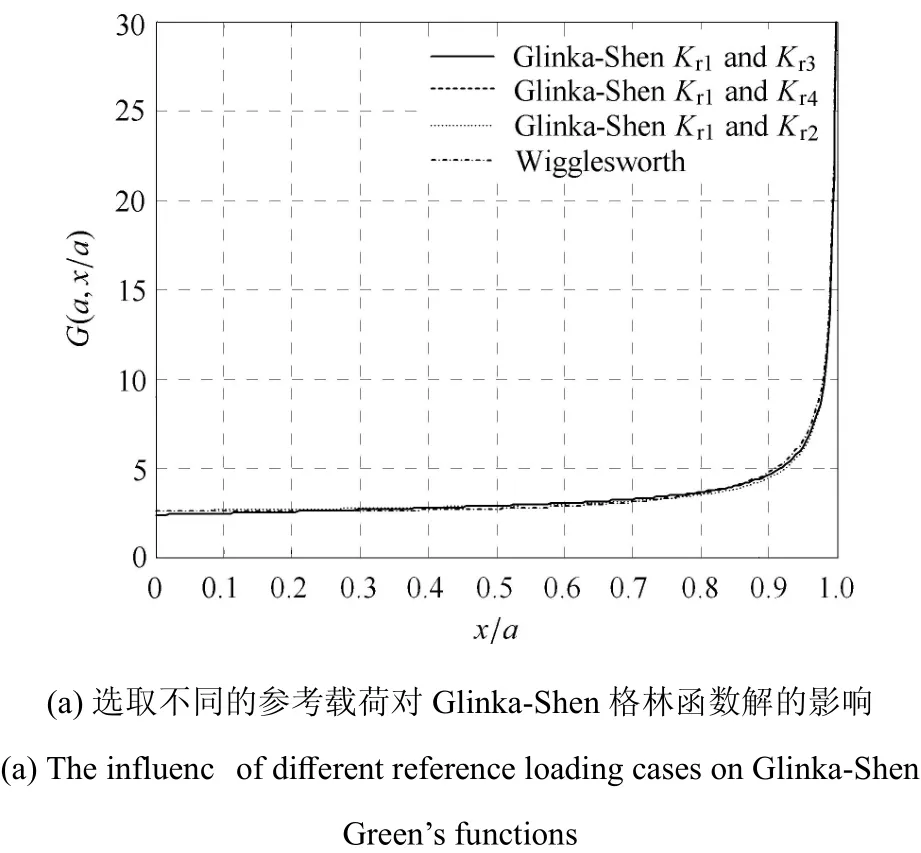
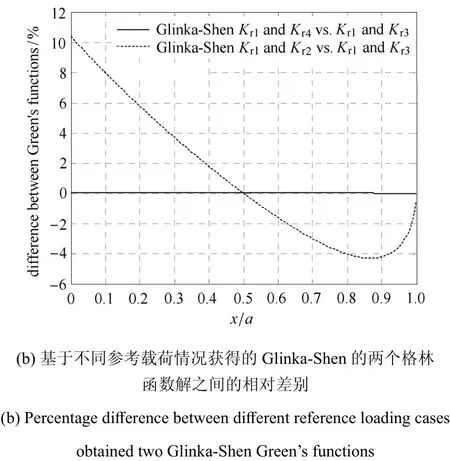
图4 选取不同的参考载荷对Glinka-Shen格林函数解的影响Fig.4 The influenc of di ff erent reference loading caseson Glinka-Shen Green’s functions

基于Wu-Carlsson权函数法[11]，将式(30)和式(31)代入式(10)和式(12)中，可以求出参考解为正向线性变化载荷情况下式(11)的系数β1～β5分别为2.0000，0.7914，2.1704，-1.6836和0.3867.将式(32)和式(33)代入式(10)和式(12)中，可以求出参考解为反向线性变化载荷情况下式(11)的系数β1～β5分别为2.0000，1.4864，-0.9096，2.0061和-0.9107，其相应的格林函数如图5(a)所示.1.1节中参考载荷为均布载荷情况下的格林函数也在图5(a)中给出.

图4表明，Glinka-Shen格林函数(基于均布载荷和正向线性变化载荷)和Glinka-Shen格林函数(基于均布载荷和反向线性变化载荷)基本一致,相对差别在0.01%以内；而均布载荷和裂纹嘴集中力进行组合得到的格林函数与均布载荷和正向线性变化进行组合得到的格林函数之间最大差别则为10.1%.图5表明，基于Wu-Carlsson权函数法，正向线性变化载荷作为参考解得到的格林函数与均布载荷情况下得到的格林函数之间最大差别为1.76%；反向线性变化载荷作为参考解得到的格林函数与均布载荷情况下得到的格林函数之间最大差别为1.31%.这说明Glinka-Shen利用两个参考解以及u′′=0的条件得到的格林函数精度明显受到所选参考载荷的影响，而不同参考载荷对Wu-Carlsson格林函数的影响则很小.

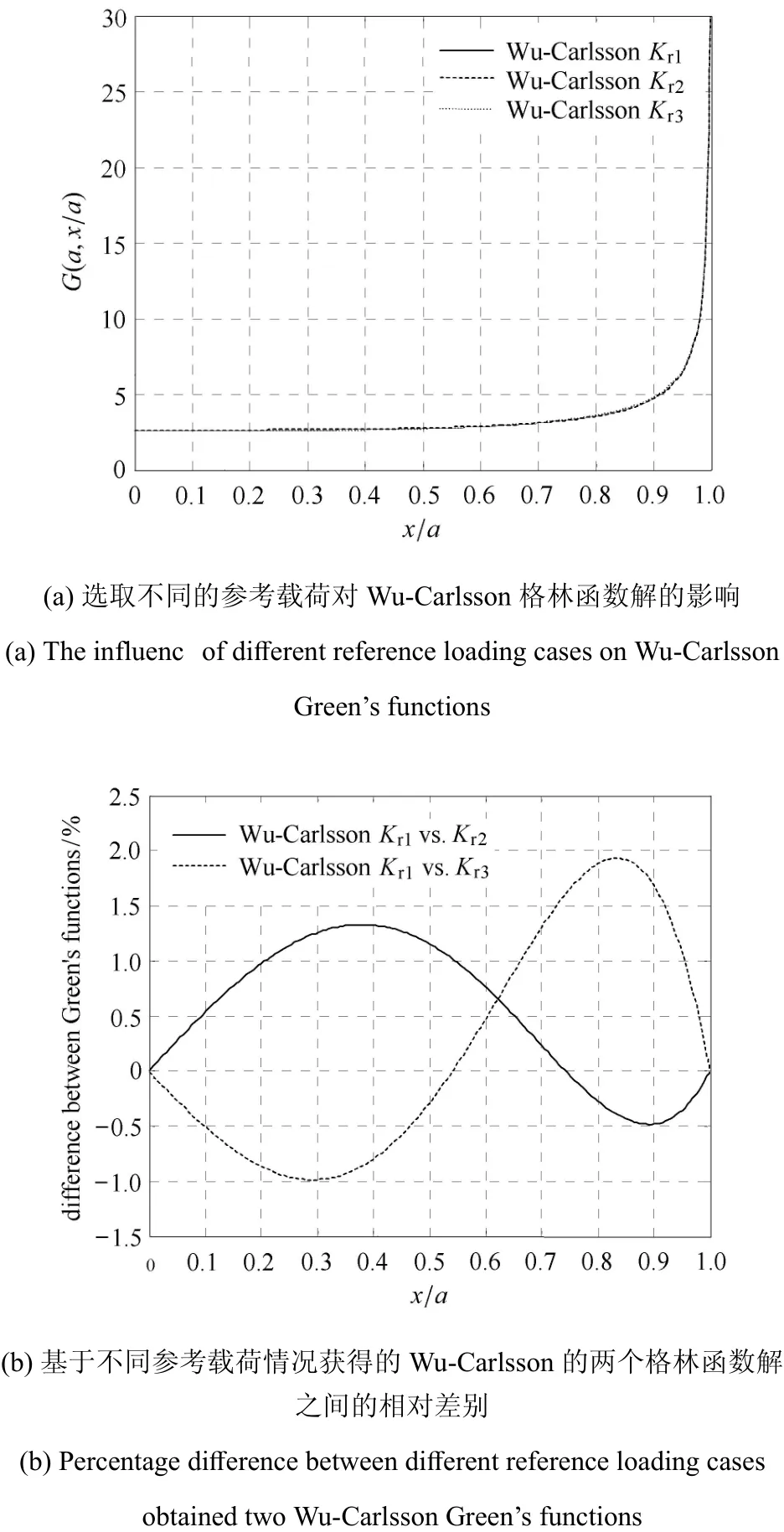
图5 选取不同的参考载荷对Wu-Carlsson格林函数解的影响Fig.5 The influenc of di ff erent reference loading caseonWu-Carlsson Green’s functions

4 条件u′′′=0对Wu-Carlsson权函数精度的影响

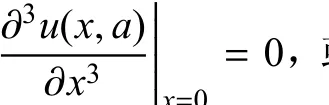
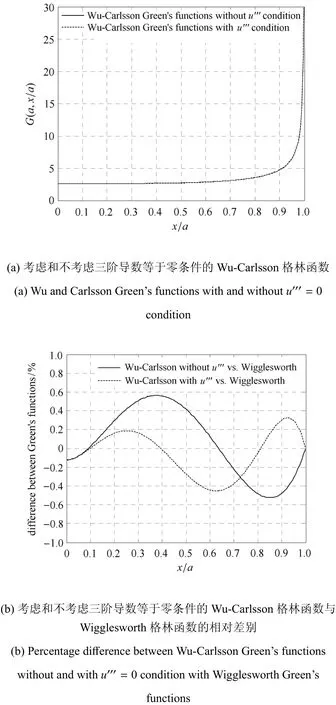
图6 考虑和不考虑三阶导数等于零条件对Wu-Carlsson格林函数解的影响Fig.6 The influenc ofw ithoutand w ith u′′′=0 condition on Wu-Carlsson Green’s functions

Wu-Carlsson权函数法[11]只用了1.1节中的4个条件.如果在这4个条件基础上再加条件u′′′=0，则求得式(3)的系数为F1～F5分别为4.4860,-0.4957,-0.6726,1.2167和-0.4210；式(11)的系数为β1～β6分别为2.0000,1.3370,-1.2784,4.6967,-4.4013和1.3138.考虑和不考虑u′′′=0条件的格林函数如图6所示.图6表明，未考虑该条件的Wu-Carlsson格林函数与Wigglesworth格林函数的最大差别为0.56%，加入该条件后则为0.45%.可见u′′′=0条件对Wu-Carlsson格林函数精度改进效果较小，因此可以舍弃.

5 半无限板边缘裂纹在各种载荷作用下的应力强度因子权函数解

针对半无限板边缘裂纹情况，基于权函数法，选取4种裂纹面受载荷情况，分别为裂纹面受幂函数载荷作用(σ(x)=σ0(x/a)n其中n=1,2,3)(如图2(e)所示)和裂纹面受反向线性分布载荷作用(σ(x)=σ0[1-(x/a)])(如图2(d)所示).分别利用上述多种权函数解，求解了这4种受载情况下的应力强度因子，并与W igglesworth[16]解进行对比，结果见表1.

表1显示,基于Wu-Carlsson,Fett-Munz,Hartranft-Sih,Bueckner的权函数解和基于Wigglesworth解得到的半无限板边缘裂纹受不同载荷情况下的应力强度因子解的相对差别整体都在1%之内；而基于Glinka-Shen权函数解得到的不同载荷情况下的应力强度因子相比其他方法误差较大，最大相对差别为3.99%.

表1 由各种权函数求得的半无限板边缘裂纹裂纹面受幂函数载荷和裂纹面受反向线性分布载荷作用下的无量纲应力强度因子Table 1 Based on di ff erentweight functionmethods,stress intensity factorsof an edge crack in a sem i-infinit plate crack surface subjected to power function load and reverse linear distributed load

6 结论

针对半无限板边缘裂纹，分析了Wu-Carlsson、Glinka-Shen和Fett-Munz这3种权函数法的求解精度.并与文献中已有的半无限板边缘裂纹的权函数进行了广泛对比，包括Bueckner权函数、Hartranft-Sih权函数(Tada手册中采用的权函数)，以及Wigglesworth利用解析手段推导出的高精度的权函数.利用上述权函数法，求解了裂纹面受幂函数加载和反向线性分布载荷作用下的应力强度因子，得到的主要结论如下：

(1)Wu-Carlsson和Fett-Munz权函数法的计算精度高于Glinka-Shen权函数法；

(2)Glinka-Shen推导出的权函数精度受到所选参考载荷的明显影响.而Wu-Carlsson权函数法，参考载荷的选取对权函数的影响则很小；

(3)u′′′=0条件对Wu-Carlsson权函数法计算精度改进效果很小,在实际分析中可以舍弃.

1 Bueckner H.Novelprinciple for the computation of stress intensity factors.ZeitschriftfuerAngewandteMathematik&Mechanik,1970,50(9)：529-546

2 Rice JR.Some remarks on elastic crack-tip stress fields International JournalofSolidsand Structures,1972,8(6)：751-758

3 Paris PC,M cmeeking RM,Tada H.The weight function method for determ ining stress intensity factors//Crack and Fracture,ASTM Special Technical Publication,1976

4 Wu XR,Carlsson J.The generalised weight function method for crack problemsw ithm ixed boundary conditions.JournaloftheMechanicsand PhysicsofSolids,1983,31(6)：485-497

5 ShenG,GlinkaG.Determ inationofweightfunctions from reference stress intensity factors.Theoretical&Applied Fracture Mechanics,1991,15(3)：237-245

6 FettT.Directdeterm inationofweight functions from reference loading cases and geometrical conditions.Engineering Fracture Mechanics,1992,42(3)：435-444

7 M illwaterH,WagnerD,BainesA,etal.ImprovedWCTSEmethod for the generation of 2D weight functions through implementation into a commercial finit element code.Engineering Fracture Mechanics,2013,109(0)：302-309

8 GlinkaG,Shen G.Universal featuresofweight functions for cracks in mode I.Engineering Fracture Mechanics,1991,40(6)：1135-1146

9 Wu XR,XuW.Strip yield crack analysis formultiplesitedamage in infinit and finit panels-A weight function approach.EngineeringFracture Mechanics,2011,78(14)：2585-2596

10 Wagner D,M illwater H.2D weight function development using a complex Taylorseriesexpansionmethod.Engineering FractureMechanics,2012,86：23-37

11 Wu X R,Carlsson AJ.Weight Functionsand Stress Intensity Factor Solutions.Oxford：Pergamon,1991

12 Fett T,Munz D.Stress intensity factors and weight functions.Southampton,UK：ComputationalMechanicsPublications,1997

13 Wu XR.Closed-form weight function foredgecrack problems.Acta Mechanica Sinica,1990,6(2)：151-159

14 Bueckner HF.Weight functions for thenotched bar.ZAMM-Journal ofApplied Mathematics and Mechanics/Zeitschriftf¨ur Angewandte Mathematik und Mechanik,1971,51(2)：97-109

15 Hartranft RJ,Sih GC.A lternatingmethod applied to edge and surface crack problems//Methods of Analysis and Solutions of Crack Problems.Netherlands：Springer,1973：179-238.

16 Wigglesworth LA.Stress distribution in a notched plate.Mathematika,1957,4(1)：76-96

17 Tada H,Paris PC,Irw in GR,etal.The Stress Analysis of Cracks Handbook.New York：ASMEPress,2000

18 FettT.Conditions for the determ ination ofapproximate COD fields Engineering FractureMechanics,1991,39(5)：905-914

WEIGHT FUNCTIONMETHODSAND ASSESSMENT FOR AN EDGECRACK IN A SEM I-INFINITE PLATE1)

Tong Dihua Wu Xueren2)Hu Benrun Chen Bo
(Beijing Institute ofAeronauticalMaterials，Beijing 100095，China)

Weight function method(WFM)is highly e ffi cient and accurate for the determination of stress intensity factors(SIFs)and crack opening displacements(CODs)of cracked bodies under arbitrary load conditions.Comparing to the numericalmethods such as the finit elementmethod,WFM s have distinct advantage in terms of computational e ffi ciency and reliability.Thispapermakessystematicanalysesand comparisonsof threeWFapproachesbyWu-Carlsson,Glinka-Shen and Fett-Munz,respectively,which are representative in the international fracturemechanicscommunity.By employing theW igglesworth analyticalsolutions to CODsofan edge crack in a sem i-infinit plateunderuniform tension,theWF and corresponding Green’s function(SIF fora pairof point forcesacting atan arbitrary location along the crack)are derived and used as the base for point-to-point comparison.The results are also compared w ith other existing WFs in the literature,including thoseby Bueckner,Hartranft-Sih andWigglesworth using di ff erentanalyticalapproaches.The study also includes the influenc of selection of three reference load cases,including uniform,linear and reverse-linearstress distributionsand their combinations,and geometric conditions related to CODson theWFaccuracy.Resultsshow that theWF based on COD analytical expression for one reference load case aremore accurate than thatbased on two SIFs due to two reference load cases.Furthermore,solution accuracy of the later approach is considerably a ff ected by the selected reference load case(s).Thegeometric condition that the third derivativeof COD vanishesatcrackmouth has littlee ff ecton the accuracy of one-reference-load-case-based weight function.Finally,SIFs for four load cases calculated by using variousWFM sare presented and compared.

sem i-infinit plate，edge crack，weight functionmethod，Green’s function，stress intensity factor

V215

A

10.6052/0459-1879-17-024

2017-01-20收稿，2017-04-07录用,2017-04-07网络版发表.

1)国家自然科学基金资助项目(11402249).

1)吴学仁，研究员，主要研究方向：材料与结构的疲劳与断裂.E-mail：xrwu621@163.com

童第华,吴学仁,胡本润,陈勃.半无限板边缘裂纹的权函数解法与评价.力学学报,2017,49(4)：848-857

Tong Dihua,Wu Xueren,Hu Benrun,Chen Bo.Weight function methods and assessment for an edge crack in a sem i-infinit plate.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(4)：848-857