等和线定理的认识及应用

潘振芹

(山东省济南市章丘中学)

根据高中数学教材知识易知,平面向量中三点共线的结论为已知为平面内两个不共线的向量,设,则A,B,C三点共线的充要条件为x＋y＝1.由于此类问题在各类试题中考查较多,且高频出现,所以本文着重给出平面向量中关于三点共线理论知识的拓展,即引入等和线定理,并通过举例加以具体说明,旨在帮助读者切实提高处理此类问题的求解能力,进一步提升直观想象等方面的数学核心素养.

1 等和线的定义

如图1所示,直线DE∥AB,C为直线DE上任一点,设

图1

(1)当直线DE经过点P时,容易得到x＋y＝1.

(2)当直线DE不过点P时,直线PC与直线AB的交点记为F,因为点F在直线AB上,所以由三点共线结论可知若(λ,μ∈R),则λ＋μ＝1.

2 等和线定理

3 应用举例

例1给定两个长度为1的平面向量它们的夹角为,如图2所示,点C在以O为圆心的圆弧AB上运 动,若(x,y∈R),则x＋y的最大值是_________.

图2

解析坐标法以O为坐标原点,所在的直线为x轴建立平面直角坐标 系,如图3所示,则点

图3

等和线法作l∥AB,且与已知圆弧相切于点D,连接OD交AB于点E.设x＋y＝k,则结合图4 易知:与直线AB平行且与圆弧有公共点的所有直线中,直线l距离圆心最远,此时k取得最大值,由图易得此时＝2.故x＋y的最大值为2.

图4

例2(2017年全国Ⅲ卷理12)在矩形ABCD中,AB＝1,AD＝2,动点P在以点C为圆心且与BD相切的圆上.若,则λ＋μ的最大值为( ).

解析坐标法建立如图5 所示的平面直角坐标系,则点C(2,1).

图5

设BD与圆C切于点E,连接CE,则CE⊥BD.因为CD＝1,BC＝2,所以

等和线法如图6所示,过动点P作等和线,设λ＋μ＝k,则k＝.由图易知,当等和线与EF(直线EF与圆C相切,切点为F)重合时,k取最大值,此时k＝

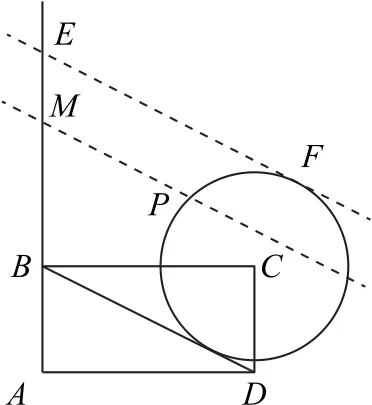
图6

又因为EF∥BD,所以＝3,即λ＋μ的最大值为3.故选A.

例3如图7所示,圆O是边长为的等边△ABC的内切圆,其与BC边相切于点D,点M为圆上任意一点,(x,y∈R),则2x＋y的最大值为( ).

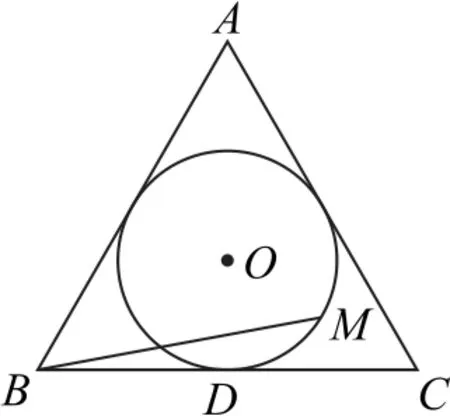
图7

解析坐标法如图8所示,连接DA,以点D为原点,BC所在直线为x轴,建立平面直角坐标系.设内切圆的半径为r,则圆心O(0,r),A(0,3),D(0,0).

图8

等和线法设内切圆与边AB相切于点E,与AC边相切于点N,易 知,如图9所示,作出值为1 的等和线DE,则AC是过圆上的点最远的等和线,此时设2x＋y＝k,则k＝＝2.

图9

从而2x＋y的最大值2.故选C.

(完)