新高考引领下一道高考切线问题引发的探究

刘江辉

(北京市首都师范大学教师教育学院)

纵观近几年的高考数学以及高考模拟题,可以发现切线问题是命题的一个热点,也是常考的一类问题,所以它成为一线教师引导学生备考的重点内容.切线问题通常以不同的知识内容作为试题背景,具有一定的综合性,有利于同时考查学生的数学核心素养.本文以一道高考真题为例,辅以变式练习,探讨此类问题的解题策略.

1 试题呈现

例(2021年新高考Ⅰ卷7)若过点(a,b)可以作曲线y＝ex的两条切线,则( ).

A.eb＜aB.ea＜b

C.0＜a＜ebD.0＜b＜ea

分析该题以指数函数作为背景,着重考查切线问题、数形结合思想及逻辑推理素养.该题打破了传统的呈现形式,检验学生灵活处理问题的能力,依据解决问题的常规思路通过数形结合把试题转化为函数零点以及函数图像交点的问题.

2 解法探究

视角1图像法

解法1图1为y＝ex的大致图像,过点(a,b)可以作曲线y＝ex的两条切线,不妨设曲线上方区域为Ⅰ区,曲线下方、x轴上方区域为Ⅱ区,x轴下方区域Ⅲ区.

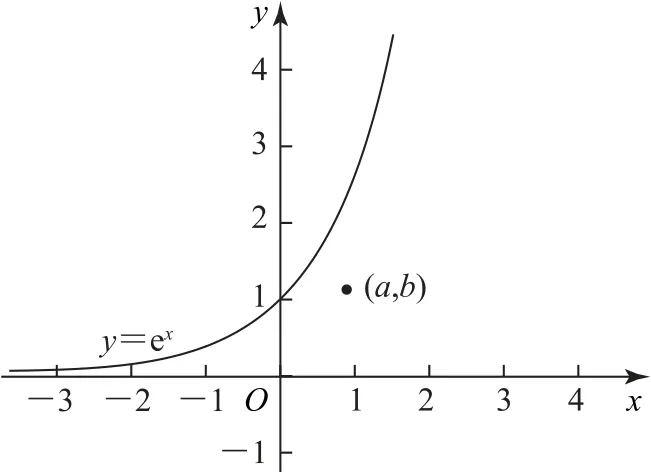
图1

当点(a,b)位于Ⅰ区时,无法作出切线;当点(a,b)位于曲线y＝ex上时,只能作出一条切线;当点(a,b)位于Ⅱ区时,能作出两条切线,且有0＜b＜ea;当点(a,b)位于x轴上时,因为x轴为y＝ex的渐近线,所以只能作出一条切线;当点(a,b)位于Ⅲ区时,只出作出一条切线.

综上,0＜b＜ea,故选D.

点评本法通过画出函数的图像,对点(a,b)的位置进行分类讨论,有助于减少运算和思维上的难度,但要求解题者具有较强的数形结合思想,因而平时要注意数学思想方法的积累.

视角2代数法

解法2设切点坐标为,因为y′＝ex,所以切线的方程为(x－x0).因为切线过点(a,b),所以(a－x0),化简可得(ax0＋1)－b＝0,则该方程有两个不同的解.

令f(x)＝ex(a－x＋1)－b,则f′(x)＝ex(ax),故f(x)在(－∞,a)上单调递增,在(a,＋∞)上单调递减,因为f(x)有两个零点,所以f(a)＞b,则b＜ea.

不妨设x1,x2为f(x)的零点,x1∈(－∞,a),x2∈(a,＋∞),则

综上,0＜b＜ea,故选D.

解法3设切点坐标为(x0,),因为y′＝ex,所以切线的方程为(x－x0).

因为切线过点(a,b),所以(a－x0),化简可得(a－x0＋1)＝b,令f(x)＝b,g(x)＝ex(a－x＋1),则函数f(x)与g(x)有两个交点.对g(x)求导有g′(x)＝ex(a－x),故g(x)在(－∞,a)上单调递增,在(a,＋∞)上单调递减,因为g(x)与f(x)有两个交点,所以b＜g(a),则b＜ea.

对于指数函数、对数函数的复合函数,我们要注意考虑它们与x轴的关系,一般用极限思想探索极端的情况.

当x→＋∞时,g(x)＜0;当x→－∞时,g(x)→0,所以b＞0.

综上,0＜b＜ea,故选D.

点评解法2和解法3都是从代数的角度出发思考问题,解法2 把问题转化为函数的零点问题,思路清晰,在证明b＞0的情况时,需要较强的发现能力.解法3把问题转化为函数图像的交点问题进行探索,难点是判断左侧函数图像的趋势,需要一定的极限思维.

3 变式拓展

变式1若过点(a,b)可以作曲线y＝lnx的两条切线,则b的取值范围是_________.

当a≤0时,f′(x)＞0在(0,＋∞)上恒成立,所以f(x)在(0,＋∞)上单调递增,不满足条件.

当a＞0 时,f(x)在(a,＋∞)上单调递增,在(－∞,a)上单调递减,所以f(x)min＝f(a)＝lna.因为g(x)＝b与f(x)的函数图像有两个交点,所以b＞lna.

点评指数函数与对数函数具有紧密的联系,改变函数的类型,运用类比的思维,将原来涉及指数函数的问题类比到对数函数中,即可得到本题,难度比原题目有所降低,却有助于对此类思想方法的领悟.

变式2若过点(a,0)可以作曲线y＝xex的两条切线,则实数a的取值范围是_________.

点评设切点坐标为(x0,x0ex0),由y′＝(x＋1)·

ex,可得切线的方程为

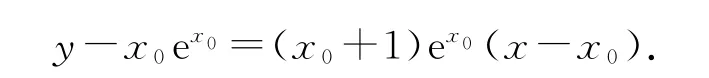
由于切线过点(a,0),故

化简得

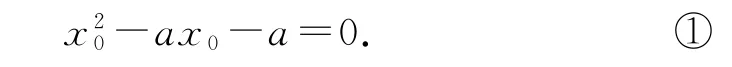
因为过点(a,0)可以作曲线y＝xex的两条切线,即方程①有两个不同的解,所以Δ＝a2＋4a＞0,解得a＞0或a＜－4.

点评对原问题进行进一步的变式拓展,融合二次函数的内容,增加问题的难度,有利于探索和归纳出解决此类问题的通性通法,为解决更高难度的问题奠定基础.

变式3已知函数f(x)＝x3－3x,过点A(1,m)(m≠－2)可以作曲线f(x)的三条切线,则m的取值范围是________.

因为过点A(1,m)可以作曲线f(x)的三条切线,所以方程①有三个不同的解.

令h(x)＝2x3－3x2＋m＋3,则h′(x)＝6x2－6x,令h′(x)＝0,解得x＝0或1.

由三次函数的图像特征可知h(x)＝2x3－3x2＋m＋3有三个零点,故h(0)h(1)＜0,即(m＋3)(m＋2)＜0,解得－3＜m＜－2.

点评三次函数是高考数学命题的重要知识点,通过思想方法的对比,以三次函数为载体,进行深层次的变式,探究切线问题,加强知识的联系,有利于强化思想方法与知识的融合,提升学生对数学知识的综合运用能力.

变式4若函数f(x)＝lnx＋(a为常数)存在两条均过原点的切线,则实数a的取值范围是________.

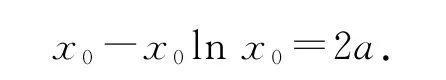
因为存在两条均过原点的切线,故x0－x0lnx0＝2a有两个不同的解.

令g(x)＝x－xlnx,h(x)＝2a,则g(x)与h(x)有两个不同的交点,对g(x)求导可得g′(x)＝－lnx,所以g(x)在(0,1)上单调递增,在(1,＋∞)上单调递减,gmax(x)＝g(1)＝1.

当x→＋∞时,g(x)→－∞,当x→0 时,g(x)→0.因为g(x)与h(x)的函数图像有两个不同的交点,所以0＜2a＜1,故0＜a＜.

点评该变式打破常规的呈现形式,在函数解析式中设置未知数以及隐性的已知条件,增加了试题内容的丰富性和价值,有助于极限数学思想方法的渗透.

一题多解可以较好地促进数学思维的培养和数学知识的融合,变式练习有助于提升学生的综合能力和数学素养.因此,在高中数学的学习过程中,学生要进一步深入关注教材中的典型问题,对其进行合理的变式研究,以期提升数学思维,提高解决问题的能力,促进学生数学核心素养的综合发展.

(完)