函数视角下2022年高考试题中的比较大小问题
谷红霞
(北京工业大学附属中学)
在数学中,比较大小的过程本质上是确定两个对象的不等关系.这类问题能考查学生的数学运算、数学抽象、直观想象等数学核心素养,应用“函数、方程与不等式”的基础知识解决问题的能力.除利用不等式的基本性质或基本不等式比较大小外,常用的方法还有特殊值法、作差(商)法、介值法、函数法.与此同时,近年来高考试题呈现出在高等数学视角下命题的趋势,这要求学生能灵活应用基础知识解决问题,也引导教师在复习备考中要深入浅出.
1 在知识体系中分析高考命题的角度
从高等数学的视角看函数,最为简朴的可以说是多项式函数,要研究一般函数在某点邻域的局部性质,可以用多项式函数局部逼近它,从而把此函数在某点的局部性质,归于这个多项式函数的局部性质去研讨.泰勒定理帮助函数实现了“局部多项式化”.
人教A 版普通高中数学教科书《必修第一册》第五章三角函数的复习参考题第26题中,提到了英国数学家泰勒发现的公式.如果用高中数学学习者的眼光看高等数学中的泰勒展开式,就是用常数与幂函数进行加减乘除运算表示分式函数、指数函数、对数函数、三角函数.而略去展开式中三次方及以上的项,一侧就出现了更为熟知的二次函数,便可以得到如下不等关系.
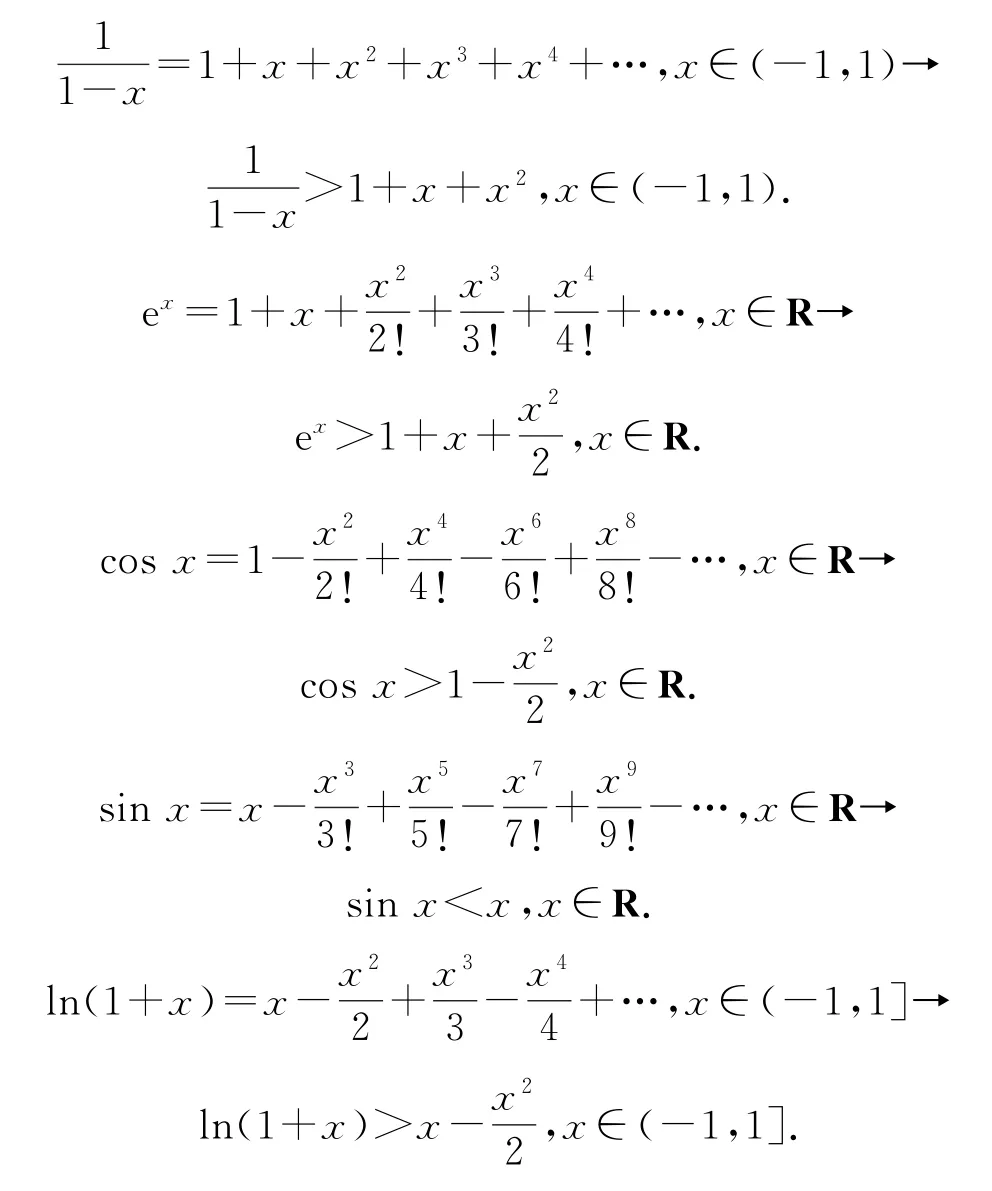
如果将不等式两侧各看作一个函数,再给定一个自变量的取值,就是两个函数对应函数值的比较,一个个比较大小的题目就出现了,如:
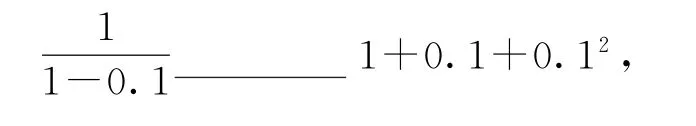
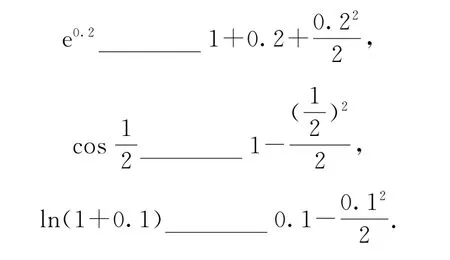
从函数图像上看,如果每个不等式中涉及的两个函数,在某点附近二者的图像几乎要“贴”在一起了,难分彼此,那么用“图像法”比较两个量的大小就非常困难.
例如,利用图1比较y=与y=1+x+x2在x=0.1处的函数值的大小;利用图2比较y=ex与y=1+x+在x=0.2处的函数值的大小;利用图3比较y=cosx与y=1-在x=处的函数值的大小;利用图4比较y=ln(1+x)与y=x-在x=0.1处的函数值的大小.这时就需要调整思路,从不同的角度构造新函数,利用导数确定函数的单调性,通过函数的单调性比较大小.
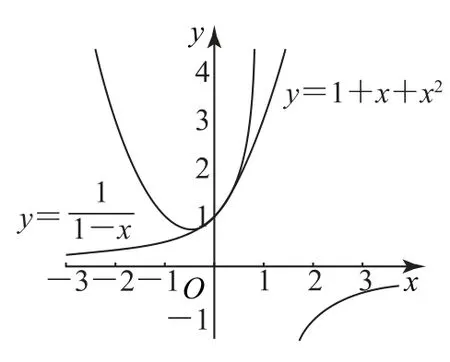
图1
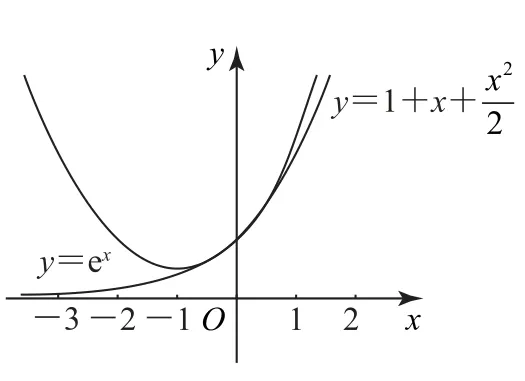
图2
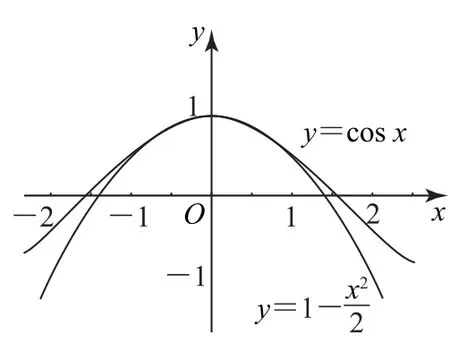
图3

图4
2 体会应用基础知识解高考真题的过程
不等式与函数的结合不仅是知识的结合,更是知识与方法的交会.通过构造函数利用函数的单调性比较大小,不仅能够迅速找到解决问题的途径,而且能够使繁杂的研究对象变得简单.这样可以很好地考查高中函数与导数的知识,而构造函数则较好地考查了数学抽象素养,解决问题的过程则考查了数学运算素养与推理论证能力.
2.1 比较结构细思量,同构异量用函数
例1(2022 年全国甲卷文12)已知9m=10,a=10m-11,b=8m-9,则( ).
A.a>0>bB.a>b>0
C.b>a>0 D.b>0>a
解析观察a与b的结构,容易想到函数f(x)=xm-(x+1),根据9m=10 等价变形得到m=log910>1.由于a=f(10),b=f(8),所以只需用导数确定函数f(x)=xm-(x+1)在(7,+∞)上的单调性.f′(x)=mxm-1-1>0(m>1)在x∈(7,+∞)上恒成立,所以原函数f(x)在(7,+∞)上单调递增,f(8)<f(9)<f(10).又f(9)=9m-10=0,所以a>0>b,故选A.
2.2 结构不同再观察,同量异构用函数
例2(2022年新高考Ⅰ卷7)设a=0.1e0.1,b=,c=-ln0.9,则( ).
A.a<b<cB.c<b<a
C.c<a<bD.a<c<b
解析显然a,b,c在结构上不具有共性,观察其对应的数字,联想到0.9=1-0.1,可以将其中的数字化异为同.故

下面比较b,c的大小,利用函数G(x)=ln(1-x)在(0,1)上单调递增,得到G(0.1)>G(0)=0,即b>c.
此时必须比较a与c的大小,可设H(x)=xex+ln(1-x),则
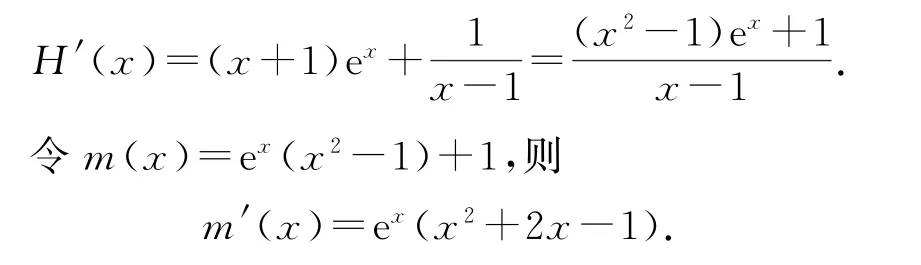
当0<x<0.1 时,m′(x)<0,函数m(x)=ex(x2-1)+1单调递减.又m(0)=0,所以m(x)<0,H′(x)>0,则H(x)单调递增,H(0.1)>H(0)=0,即0.1e0.1>-ln0.9,所以a>c.
综上,选C.
2.3 常见函数心中系,量变形变有联系

3 从解题实践中提炼的方法
3.1 理解学生,总结经验
要鼓励学生积极探讨解题思路,给予学生试错的机会.如解例3 时有学生先考虑b=cos,c=4sin,构造函数f(x)=cosx-4sinx,想利用f(x)在(0,)上单调递减进行比较.由可得,但,所以这个函数不利于比较大小.也有学生令a==1-4×()3,设函数g(x)=cosx-(1-4x3),考虑利用g(x)的单调性求解,但g′(x)=-sinx+12x2,不容易判断导函数的正负.这些想法的产生是自然的,值得肯定.但从另一方面看,这个构造函数的思考过程过于片面,显然对知识间联系的认识不够.
3.2 用好教材,一题多解
在高三复习时,利用教材中的题目,从不同的角度分析问题,打破原有学习过程中知识模块间的壁垒,可以启发学生创造性地应用知识解决问题.教材中有指数函数、对数函数比较大小的例题和习题,可以借助不同题目,体会用函数的单调性比较大小的优越性.如题目“比较log23,log34,log45 的大小”,可以通过结构上的相似性让学生尝试构造函数.将三个量分别等价变形为,则只需研究函数y=在[2,+∞)上的单调性.易知y=在[2,+∞)上是减函数,于是得到如果说一题多解可以打开思路,让人豁然开朗,那么不同时期讲解同一道题就意在突出不同的知识与方法,则耐人寻味.
3.3 关注思维,教之以法
解题应着眼于思考,正如约翰·杜威在《How We Think》的开篇中谈到的:思维的缘由是遇到了某种困惑或怀疑.思维需要引导以实现价值;思维需要经常调节以避免轻信;思维需要通过调节使推理成为证明.
首先,保有好奇心.通过观察弄清问题或困难是什么;从局部、凌乱的信息出发,联想、分析、推测,直至了解整体的情况.让好奇心成为整个过程的源动力.
其次,经常联想.在解题中,要思索,尤其是推测、联想出可能的解决方法.而联想有快有慢、有宽有窄、有深有浅,没有好坏之分,久而久之便有了“方向感”.
最后,有条理性地表达和总结.在解题后,不仅做到有条理地表达清楚,还要总结成败经验.此时仍要进行观察,吸取教训,吃一堑长一智.结合已有经验中的不足,将最初看起来相互分离的条件连接到一起,这个过程好似各自归位却又浑然一体.
(完)

