巧选视角切入,妙用方法证明
——2022年高考数学全国甲卷第23题
高生军
(黑龙江省大庆市东风中学)
不等式证明是数学问题中的重难点,其证明过程无固定的模式,证明的技巧性强,推理过程复杂,证明方法又多种多样.本文结合一道高考真题,发散思维,多方法切入,展示常规证明方法.
1 真题呈现
题目(2022年全国甲卷理23)已知a,b,c均为正数,且a2+b2+4c2=3,证明:
(1)a+b+2c≤3;
(2)若b=2c,则
分析此题涉及二元与三元不等式证明,是不等式应用中具有一定典型性的一类问题.此题的求解关键是巧妙利用条件a2+b2+4c2=3,第(2)问还可以直接利用第(1)问的结论与条件b=2c,通过合理转化与变形,进而利用不等式的性质、重要不等式等分析,特别要注意对应重要不等式的限制与条件.
2 真题破解
(1)方法1 (作差比较法)
由于a,b,c均为正数,且a2+b2+4c2=3,而
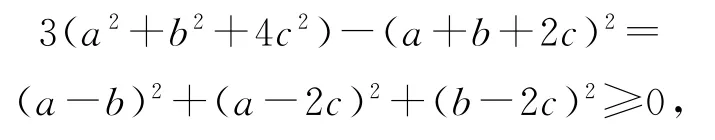
则(a+b+2c)2≤3(a2+b2+4c2)=3×3=9,即a+b+2c≤3,当且仅当a=b=2c=1时,等号成立,所以a+b+2c≤3.
点评根据题目条件中的关系式与所证关系式之间的联系,借助作差比较法求解.作差比较法简单易懂,关键是系数的合理配凑、代数式的重新组合与完全平方公式的应用等.
方法2 (基本不等式法)
由于a,b,c均为正数,且a2+b2+4c2=3,所以
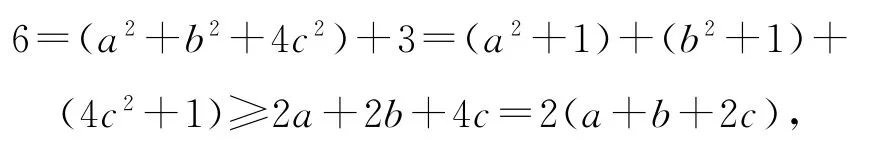
当且仅当a2=1,b2=1 且4c2=1,即a=b=2c=1时,等号成立,解得a+b+2c≤3.
点评根据题目条件中的关系式,合理配凑常数,结合所证关系式的结构特征进行组合,借助基本不等式进行放缩处理,再通过求解不等式来达到证明的目的.运用基本不等式法求解或证明问题,关键是对比条件与结论之间的联系正确配凑系数.
方法3 (柯西不等式法)
由于a,b,c均为正数,且a2+b2+4c2=3,根据柯西不等式可得(12+12+12)[a2+b2+(2c)2]≥(a+b+2c)2,则(a+b+2c)2≤3×3=9,即a+b+2c≤3,当且仅当a=b=2c=1时,等号成立,所以
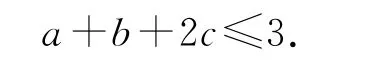
点评由于题目条件中的关系式与所证关系式的结构特征符合柯西不等式的应用条件,因此合理配凑相关的系数,利用柯西不等式加以转化,结合不等式的性质进行求解.柯西不等式是解决含多变元平方关系式的最值问题比较常用的一种技巧.
方法4 (三角换元法)

点评对题目条件中的关系式进行两次三角换元处理,再利用三角函数关系式的恒等变形与辅助角公式、三角函数的图像与性质确定代数式的最值问题,这是解决问题常用的一种技巧.三角换元法可以将代数式转化为三角函数关系式,巧妙借助三角函数的相关知识来确定最值、取值范围,从而求解不等式的证明等问题.
(2)方法1 (基本不等式法)
由于a,b,c均为正数,且b=2c,由(1)知a+b+2c=a+4c≤3,即0<a+4c≤3,根据基本不等式可得
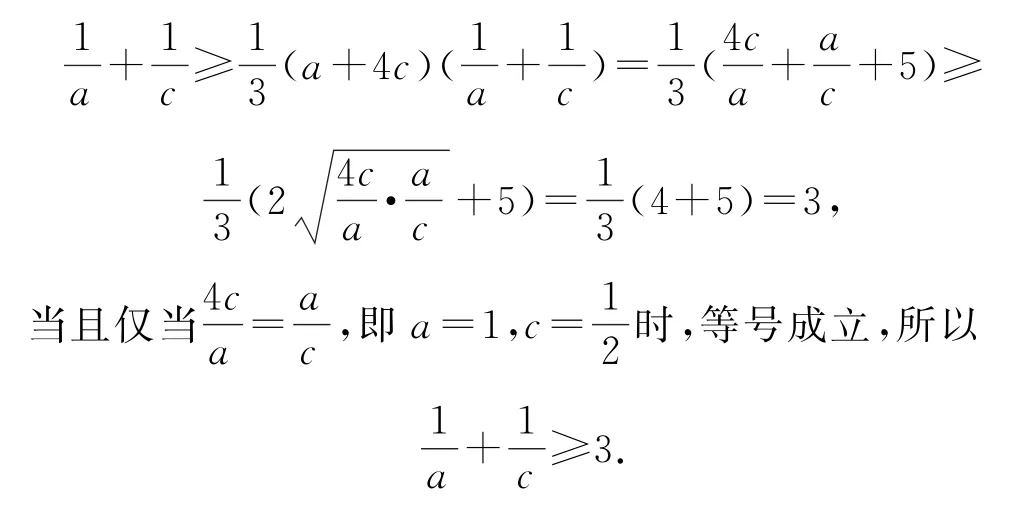
点评借助前面证明的不等式对所证分式不等式进行放缩处理,配凑出两个和式的乘积,再利用基本不等式法进一步放缩,进而巧妙证明对应的不等式.基本不等式法是处理双变元代数式的最值、取值范围或不等式成立问题常用的一种技巧.
方法2 (均值不等式法)
由于a,b,c均为正数,且a2+b2+4c2=3,b=2c,则a2+8c2=3,根据均值不等式可得
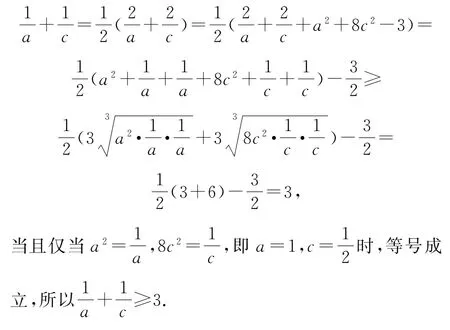
点评对已知条件消元处理,借助组合与配凑技巧将不等式配凑成三元均值不等式的形式,进而利用三元均值不等式求解.涉及三元及其以上的均值不等式法应用,关键是正确的组合与合理的配凑.
方法3 (权方和不等式法)
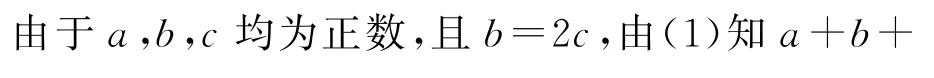

点评先对不等式进行合理的系数配凑与转化,再利用权方和不等式进行求解.权方和不等式是解决含分式关系式的最值问题比较常用的方法,求解的关键是对不等式的形式和系数进行配凑与转化.
方法4 (三角换元法)

点评先进行三角换元处理,再利用权方和不等式加以合理放缩,通过等号成立的条件确定对应的三角函数值,进而证明对应的不等式.利用三角换元法解题时,有时直接利用三角恒等变换或三角函数的相关知识,有时要结合重要不等式合理放缩.
3 小结
求解不等式问题,关键是熟练掌握基本的常规证明方法,在此基础上可以合理选用一些技巧方法.只有深刻理解与掌握不等式的实质,熟练掌握一些重要不等式以及常用的证明方法(如作差或作商比较法、三角换元法等),才能灵活应用,发散思维.
(完)

