多思维切入,妙视角拓展
——2022年高考数学新高考Ⅱ卷第12题
陈耀熙
(福建省福州超德中学)
以多选题为创新形式的不等式成立的判断问题,是近年新高考数学试卷中的一类常考的热点题型,难度中等及以上.此类问题背景简洁、情境多变、创设新颖,合理交会、融合函数与方程、不等式等相关知识,合理融入数学抽象、数学运算、逻辑推理等核心素养,全面考查数学基本知识、数学思想方法和数学能力,备受各方关注.本文从不等式思维、整体思维、换元思维以及特殊思维等不同思维方式,对2022年数学新高考Ⅱ卷第12题进行分析与深入研究,归纳总结了不同的解题方法与技巧,展示思维方式与能力的要求,突出创新意识与创新应用,以期引领并指导高考数学备考与解题研究.
1 真题呈现
题目(2022年新高考Ⅱ卷12,多选题)若实数x,y满足x2+y2-xy=1,则( ).
A.x+y≤1
B.x+y≥-2
C.x2+y2≤2
D.x2+y2≥1
分析此题是多选题,它以二元方程为问题背景,结合不等式成立的判断来设置,主要考查函数与方程、不等式等相关知识.
试题难度中等,属于比较常见的题型,只是这里借助多选题的形式加以创新编制.解题时,可以巧妙地运用融入整体思维以及换元思维,实现问题的分析与判断.
2 真题破解
2.1 不等式思维
方法1 (不等式性质法)
由x2+y2-xy=1,可得(x+y)2-3xy=1,由不等式性质可得,则

综上,选BC.
点评根据二次函数的性质及其对应的展开式,对代数式进行配方与转化,再结合不等式的相关知识来确定代数式x+y,x2+y2等的取值范围,从而分析与判断选项.不等式思维是分析与判断此类问题中常用的思维,关键是把握不等式的性质,提升数学运算、逻辑推理等素养,从而巧妙变形,正确判断.
2.2 整体思维
方法2 (配方法)
由x2+y2-xy=1,配方可得
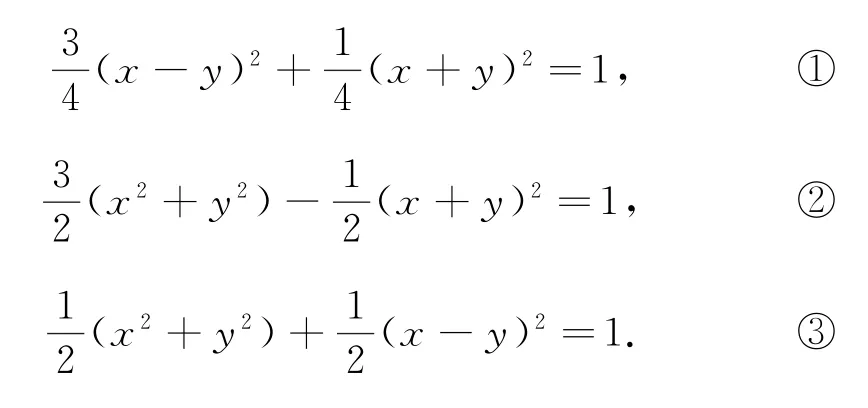
点评熟悉代数式x+y,x-y,xy,x2+y2等之间的关系,合理恒等变形与化归,利用代数式的结构特征确定对应的不等式,为求解相应代数式的取值范围提供了条件.运用整体思维法处理此类问题时,对代数式的变形与转化以及数学运算能力的要求比较高,要求学生有敏锐的洞察力与运算技巧.
2.3 换元思维
方法3 (对称换元法)

点评引入双变元进行对称换元处理,将条件中的二元方程转化为关于新参数的关系式,进而确定对应的取值范围,从而得以分析与判断.对称换元法是破解复杂二次方程中比较常用的一种变换技巧,其以新参数代替原参数,简化关系式,优化过程.
2.4 特殊思维
方法4 (特殊值法)
取特殊值令x=y=1,其满足x2+y2-xy=1,则x+y=2≤1不成立,故选项A 错误;再取特殊值x=-y=,其满足x2+y2-xy=1,则x2+y2=≥1不成立,故选项D 错误.再根据多选题的特征,故选BC.
点评通过选取二元方程满足条件下的特殊值,合理排除选项.在多选题中,尤其是确定其中两个选项错误时,则另外两个肯定是正确答案.利用特殊值法破解相应的综合与创新问题,有一定的“秒杀”效果,但一般“可遇而不可求”,不具有可推广性与普及性,如果一定要花大量时间去配凑特殊值,有可能会得不偿失.
3 变式拓展
通过改变题目中变量的取值情况,赋予新的情境,对问题进行变式拓展,并通过问题的分析与求解巩固解题方法.
变式(多选题)已知a>0,b>0,且a+b=2,则下列不等式对一切满足条件的a,b恒成立的是( ).

4 小结
4.1 掌握“通技通法”,巩固“四基”训练
高考中涉及不等式成立的判定问题,主要融入函数与方程、不等式等相关知识.常见解决问题的通性通法是不等式思维、整体思维、换元思维、特殊思维等,借助一些常见的方法(如配方法、特殊值法等),全面灵活应用相关的数学知识来分析与解决问题,巩固数学“四基”训练.
4.2 体验思想方法,培养核心素养
高考中涉及不等式成立的判定问题,巧妙设置,创新应用,融入函数与方程、化归与转化以及特殊与一般等数学思想方法,渗透相应的数学能力及数学抽象、逻辑推理、直观想象、数学运算等数学核心素养,使学生在解题过程中掌握和领悟数学思想方法,培养学生的数学核心素养.
(完)

