例谈基本不等式在高考中的应用
谢文龙
(云南省下关第一中学)
基本不等式的应用是近几年高考考查的热点,基本不等式主要用于判断数值的大小、求解取值范围以及最值,这类问题题型较多,重点考查学生利用所学知识解决问题的能力.
1 利用基本不等式比较大小

综上,a>b>c,故选A.
点评本题主要考查了学生利用基本不等式比较大小,考查学生分析问题和解决问题能力,解题的关键在于基本不等式的应用.
变式已知a=log75,b=log97,c=1.110.1,则a,b,c的大小为( ).
A.c<a<bB.a<b<c
C.b<a<cD.c<b<a
解析先分析得到c>1,0<a<1,0<b<1,再利用作差法结合基本不等式判断a,b的大小.c=1.110.1>1.110=1,a=log75<log77=1,
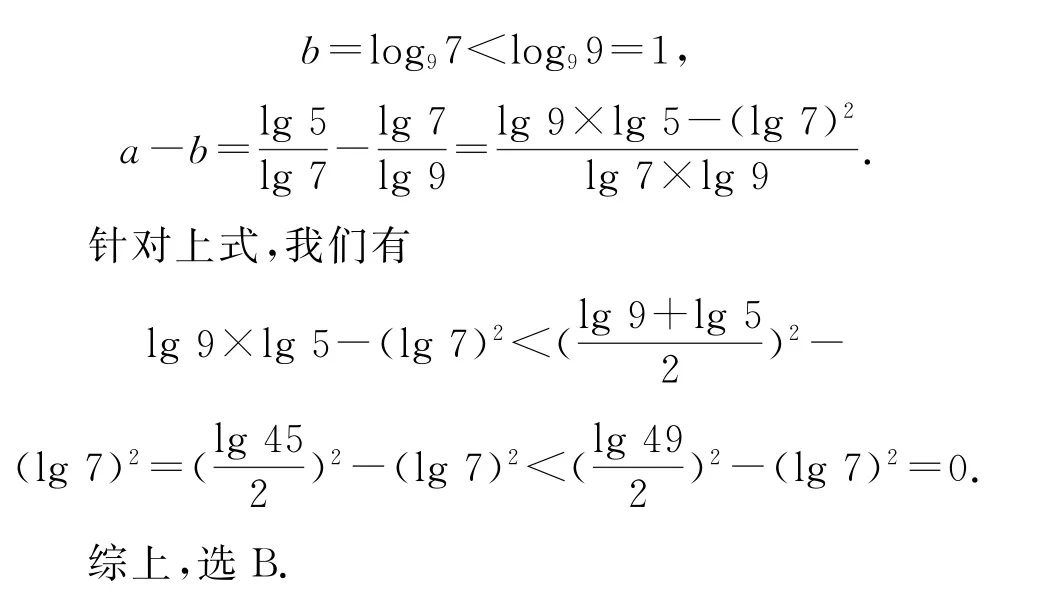
2 利用基本不等式求范围
例2(2022 年新高考Ⅱ卷12,多选题)若实数x,y满足x2+y2-xy=1,则( ).
A.x+y≤1 B.x+y≥-2
C.x2+y2≤2 D.x2+y2≥1
解析因为,而x2+y2-xy=1可变形为(x+y)2-1=3xy≤3)2,解得-2≤x+y≤2,当且仅当x=y=-1 时,x+y=-2,当且仅当x=y=1时,x+y=2,所以A 错误,B正确.
对x2+y2-xy=1变形可得
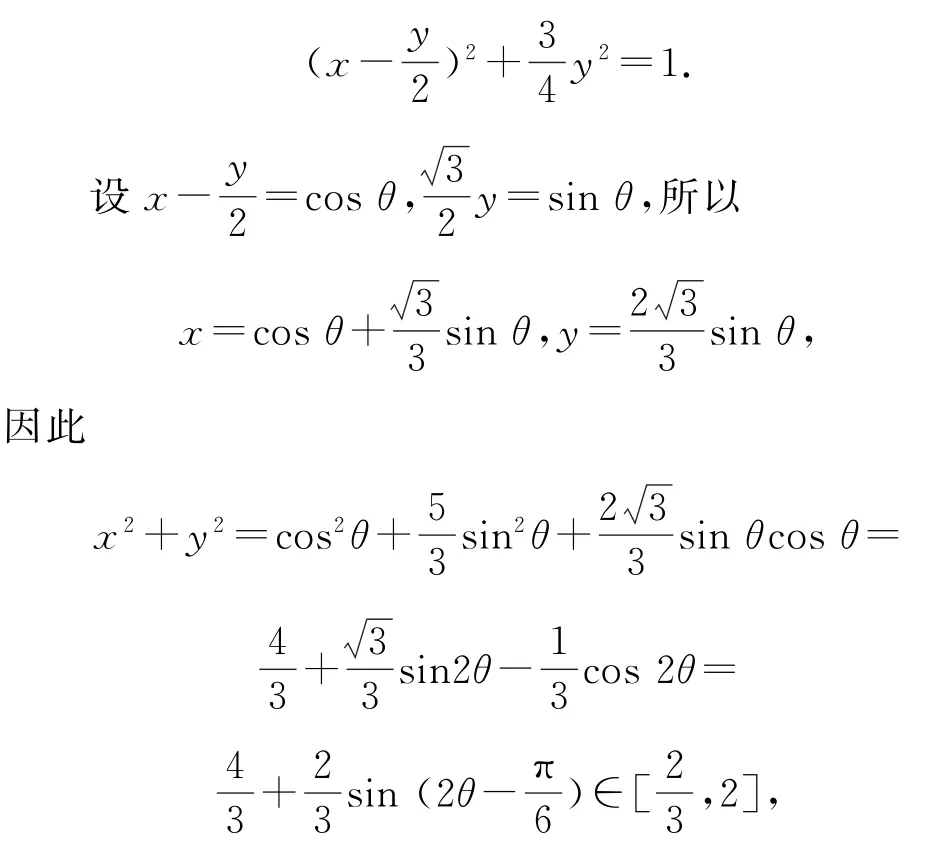
所以C正确,D 错误.
综上,选BC.
点评本题考查了利用基本不等式求范围,考查学生对于基本不等式和重要不等式的应用以及转化能力.
变式1若a>0,b>0,且a+b=2,则下列不等式恒成立的是( ).

综上,选D.
变式2(多选题)已知a,b∈(0,1),且a+b=1,则( ).
A.a2+b2≥
B.lna+lnb≤-2ln2
C.lnalnb≥(ln2)2
D.a+lnb<0
解析利用基本不等式可判断选项A;利用基本不等式结合对数函数的单调性可判断选项B;利用特殊值法可判断选项C;构造函数f(x)=1-x+lnx,利用函数f(x)在(0,1)上的单调性可判断选项D.
对于选项A,因为1=(a+b)2=a2+b2+2ab≤2(a2+b2),所以a2+b2≥,当且仅当a=b=时,等号成立,故A 正确.

对于选项D,令f(x)=1-x+lnx(0<x<1),则f′(x)=>0,所以f(x)在(0,1)上为增函数,因为0<b<1,则f(b)=1-b+lnb=a+lnb<f(1)=0,故D 正确.
综上,选ABD.
3 利用基本不等式求最值
例3(2022年全国甲卷理16)已知△ABC中,点D在边BC上,∠ADB=120°,AD=2,CD=2BD.当取得最小值时,BD=_________.

例4(2022年新高考Ⅰ卷18)记△ABC的内角A,B,C的对边分别为a,b,c,已知


变式3在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为________.

当且仅当c=2a=3时,等号成立,则4a+c的最小值为9.
(完)

