不等式恒成立,双参取值范围——2022年高考数学浙江卷第9题

尹淑华

(山东省济南市章丘区第五中学)

含多个参数的不等式恒成立问题,是高考数学浙江卷中的一种特色题型,主要考查数学知识与数学能力等.本文结合一道含参绝对值不等式恒成立的综合创新题,拓展解题方法,链接高考真题,充分展示问题的内涵与外延,以期指导数学备考与解题研究.

1 真题呈现

例1(2022年浙江卷9)已知a,b∈R,若对任意x∈R,a|x－b|＋|x－4|－|2x－5|≥0,则( ).

A.a≤1,b≥3 B.a≤1,b≤3

C.a≥1,b≥3 D.a≥1,b≤3

2 真题剖析

此题以含双变参的绝对值不等式恒成立创设情境,题目条件简洁明了,求解时需要借助恒成立的绝对值不等式来确定双变参的取值范围,而双变量之间的函数关系以及不等式恒成立关系导致问题具有复杂性与多变性.

3 真题破解

3.1 函数思维

方法1 (图像直观分析法)

由a|x－b|＋|x－4|－|2x－5|≥0,可得a|x－b|≥|2x－5|－|x－4|,作出函数f(x)＝|2x－5|－|x－4|＝的图像,如图1 中实线部分所示,而a|x－b|≥f(x),结合函数y＝a|x－b|的图像(如图1 中虚线部分),可知1≤b≤3且a≥1.

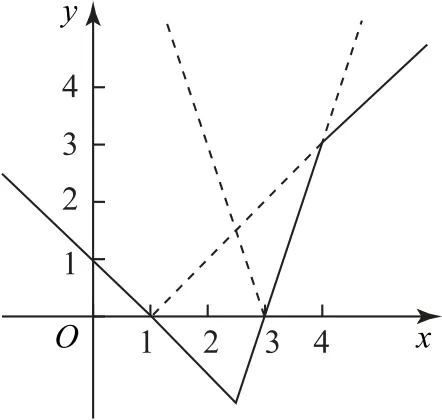
图1

结合各选项中的数据信息可知a≥1,b≤3,故选D.

点评对题目条件中的绝对值不等式进行恒等变换、分离参数,构建函数并作出函数的图像,利用含参函数图像的极端点效应,借助数形结合思想方法确定双参数的取值范围.

方法2 (函数最值分析法)

设函数f(x)＝a|x－b|＋|x－4|－|2x－5|,x∈R,要使得f(x)≥0在R上恒成立,则a＞0,否则f(0)＝a|b|－1＜0.选取x＝b,由f(b)＝|b－4|－|2b－5|≥0,可得|b－4|≥|2b－5|,两边同时平方整理可得(b－1)(b－3)≤0,解得1≤b≤3,排除选项A和C.

科学家分析了超过13.3万人的数据。结果发现，每周服用325毫克标准剂量阿司匹林2片或更多，患原发性肝细胞癌的风险降低49%；服用5年以上，风险降低59%。研究显示，服用阿司匹林越久，患肝癌风险降低得越多。但停药后，其效果会逐渐减退。停药8年后，这种益处就消失了。

点评根据题目条件中的绝对值不等式恒成立整体构建函数,利用不等式恒成立确定参数a为正数.选取特殊值进行消参处理,通过求解不等式确定参数b的取值范围,由此加以排除,并利用函数的最值情况进一步确定参数a的取值范围.抓住函数思维,利用函数与不等式之间的关系、函数最值等来转化与应用.

3.2 反证法思维

方法3 (反证法)

若a＜1,则当x→＋∞时,可得a|x－b|＋|x－4|－|2x－5|＝a(x－b)＋(x－4)－(2x－5)＝(a－1)x－ab＋1＜0,这与条件a|x－b|＋|x－4|－|2x－5|≥0矛盾,故有a≥1.

若b＞3,则当x＝b,3＜b＜4时,有a|x－b|＋|x－4|－|2x－5|＝|b－4|－2b＋5＝9－3b＜0;当x＝b,b＞4时,有a|x－b|＋|x－4|－|2x－5|＝|b－4|－2b＋5＝1－b＜0,这与条件a|x－b|＋|x－4|－|2x－5|≥0矛盾,故有b≤3.

综上,可知a≥1,b≤3,故选D.

点评根据题目条件中绝对值不等式恒成立,通过假设两变参的取值范围,结合自变量的特殊取值情况加以分析,推理分析得出与条件产生矛盾的结论,进而确定参数的取值范围.

3.3 极端思维

方法4 (极端效应法)

当x→＋∞时,由a|x－b|＋|x－4|－|2x－5|≥0,可得a(x－b)＋(x－4)－(2x－5)≥0,整理有(a－1)x≥ab－1(常数),则a－1≥0,即a≥1.

选取特殊值x＝b,由a|x－b|＋|x－4|－|2x－5|≥0,可得|b－4|≥|2b－5|,两边同时平方并整理可得(b－1)(b－3),解得1≤b≤3.

综上,可知a≥1,b≤3,故选D.

点评根据题目条件中绝对值不等式恒成立的条件,通过分析自变量取正无穷的极端效应,确定参数a的取值范围,再利用特殊值法构建含参数b的不等式,进而求解不等式确定参数b的取值范围.

3.4 特殊思维

方法5 (特殊值验证法)

选取特殊值x＝4,则由a|x－b|＋|x－4|－|2x－5|≥0,可得a|4－b|－3≥0,显然a≠0且b≠4,观察各选项可知只有a≥1,b≤3符合这个结论,故选D.

点评选取特殊值代入题目条件中的绝对值不等式,通过含参不等式恒成立确定对应参数的取值情况,并结合各选项中的参数取值范围加以验证.借助特殊值法解题时有可能不能直接确定对应参数的取值范围,这时需要根据选项中各相关参数的不同取值范围加以验证与判断.

4 链接高考

以双变参的不等式恒成立创设问题情境,是高考数学浙江卷的一种特色题型,在以往高考浙江卷中也出现过,只是变换了不等式的类型.

例2(2020年浙江卷9)已知a,b∈R 且ab≠0,对于任意x≥0均有(x－a)(x－b)(x－2a－b)≥0,则( ).

A.a＜0 B.a＞0

C.b＜0 D.b＞0

解析当a＝b＝－1时,代入条件关系式可得(x＋1)(x＋1)(x＋3)≥0在x≥0上恒成立,此时a＜0且b＜0.当a＝1,b＝－1时,代入条件关系式得(x－1)2(x＋1)≥0在x≥0上恒成立,此时a＞0且b＜0,至此,可以排除选项A,B.

当a＝－1,b＝1时,代入条件关系式可得(x－1)(x＋1)2≥0在x≥0上不恒成立,此时a＜0且b＞0,至此,可以排除选项D.

综上,选C.

点评当然,该问题的破解还可以利用三次函数的图像与性质求解,或借助不等式思维,利用不等式的性质或不等式组的求解分类讨论等.

5 小结

5.1 联系知识,形成网络

函数、方程与不等式这三者之间,往往各自独立又相互联系,经常可以加以恒等变形与巧妙转化,实现不同知识点之间的跨越,从而形成这三者之间的网络体系与综合应用.借助问题的设置与知识的联系,构建整个数学知识网络体系,全面整合,综合应用.

5.2 重视基础,提升能力

对于此类含参不等式恒成立的综合创新应用问题,实际解决过程中要正确挖掘题目条件,做到心中有“数”.在平时数学学习过程中,重视数学基本功底的巩固与训练,重视数学思维层面的发散与提升,通过研究典型问题的通性通法,才能以不变应万变.此外,在解题训练中要将基本功底融入解题活动中,将基本方法上升至思维方法与数学能力的层面.

(完)