浅谈向量外积在中学数学中的几个应用

李志军

(湖南省长沙市中雅培粹学校)

向量理论具有深刻的数学内涵、丰富的物理背景.向量既是代数研究对象,也是几何研究对象,是沟通几何、代数和三角的桥梁.高中阶段主要学习向量的内积(数量积),其运算结果是数,即a·b＝|a||b|·cosθ,其中θ为向量a,b的夹角,0≤θ≤π,其值为a的长度|a|与b在a方向上的投影长|b|cosθ的乘积,或b的长度|b|与a在b方向上的投影长|a|cosθ的乘积.向量还有另一种形式的乘法,即外积(叉积),其运算结果是一个向量.本文对向量的外积进行简单介绍,并介绍向量的外积在中学数学中的几个重要应用,旨在拓宽学生数学视野,更好地了解和运用向量的外积,并运用它解决实际问题,体会运用不同的方法带来的相同效果,感受数学的美和真.

1 向量外积的定义

在三维空间中,两个向量的外积既可以自然地描述,也可以用坐标来定义.向量外积(也称为叉积),其运算结果还是一个向量,即若c＝a×b,则c的方向与两向量a,b都垂直,大小为以|a|,|b|为邻边的平行四边形面积,即|a||b|sinθ(θ为向量a,b的夹角).向量的外积在解决几何问题时,同样发挥着非常重要的作用.通常采用“右手法则”判断a×b的方向,即右手四指由a的方向转向b的方向时,大拇指所指的方向即为a×b的方向,如图1所示.

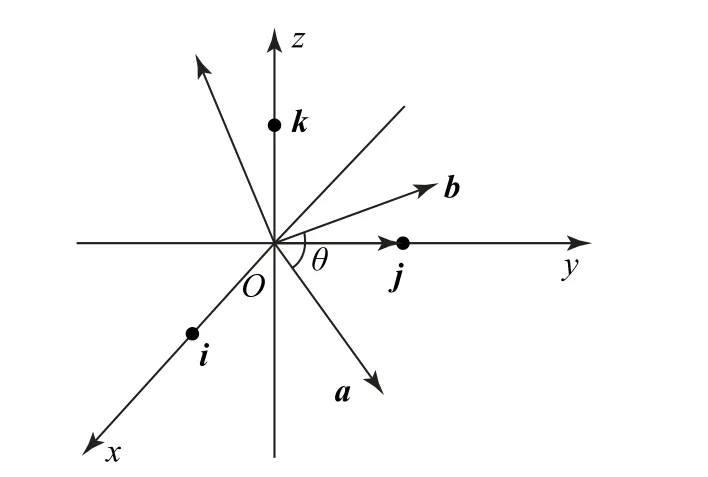
图1

2 如何求两向量的外积

如图1所示,若i,j,k分别为x轴,y轴和z轴的正向单位向量,根据向量的外积定义有

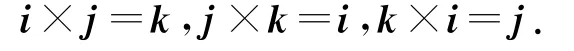
选定空间中一组直角坐标系,i,j,k为对应的三个正交单位向量.若a＝a1i＋a2j＋a3k,b＝b1i＋b2j＋b3k,a×b可以将a,b看作两个多项式,像多项式乘以多项式一样,其中

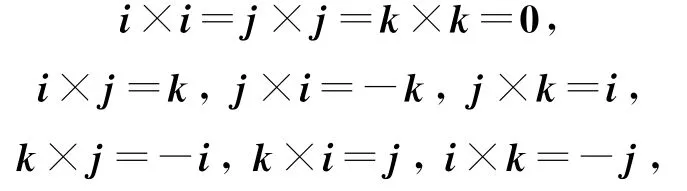
则

上述结果记忆起来太费劲,也太复杂,根据行列式的基本运算法则,a×b还可以表示为

利用行列式符号来表示向量的外积不仅方便记忆和运算,还可以利用行列式的性质来验证一些向量外积的性质.

上面计算向量外积的方法各有千秋,前者易懂,后者好算,可以通过机械运算来验证一些复杂的式子,比如验证Jacobi恒等式:(a×b)×c＋(b×c)×a＋(c×a)×b＝0,若用前者方法运算,过程烦琐且容易出错,但用行列式来表示向量的外积,利用行列式的有关性质计算,就容易很多,有兴趣的读者不妨试一试.

3 外积的几个性质

3.1 (a×b)·a＝(a×b)·b＝0

由行列式的性质可知,将i,j,k分别用a1,a2,a3或b1,b2,b3代替,此时行列式①的值等于0,也就是说,a×b与a,b都垂直.也可以根据向量外积的定义进行证明,由向量外积的定义可知a×b与a,b都垂直,又因为两垂直向量的内积为零,所以(a×b)·a＝(a×b)·b＝0,显然结论成立.

3.2 |a×b|＝|a||b|sinθ

θ为a,b两个向量所夹的小于或等于180°的非负角,与坐标系的选取无关,a×b是模长为|a||b|·sinθ,且与a,b都垂直(正交)的向量,|a||b|sinθ是以|a|,|b|为邻边的平行四边形的面积.因为

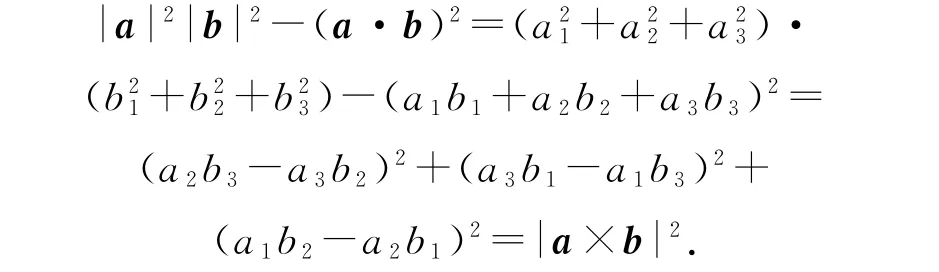
又因为a·b＝|a||b|cosθ,代入后两边开方得|a×b|＝|a||b|sinθ,所以|a×b|＝|a||b|sinθ,所以当a,b中有一个为零,或者两向量平行时,有a×b＝0.

3.3 外积的运算

外积的运算与一般的乘积运算有相同之处,也有不同之处.相同的是分配律成立,如a×(b＋c)＝a×b＋a×c,(b＋c)×a＝b×a＋c×a.不同的是交换律与结合律并不成立,如a×b≠b×a,(a×b)×c≠a×(b×c)等.显而易见,向量的外积运算不满足交换律,即a,b的外积与次序有关,即a×b并不等于b×a,而是a×b＝-b×a.如将a＝i,b＝j,c＝k分别代入(a×b)×c和a×(b×c)中,发现其并不相等.

4 外积的几个应用

外积在解题和证明有关问题时十分有效.比如,求给定坐标的多边形面积、多面体的体积以及长度和夹角问题,再比如,证明几何和三角恒等式中的有关命题和定理,直观明了,如已知a＋b＋c＝0,求证:a×b＋b×c＋c×a＝0,利用外积的定义证明就一目了然.下文列举几个利用外积的方法解决中学数学问题的例子.

4.1 正弦定理

正弦定理的证明有多种方法,如面积法、坐标法、向量的数量积以及利用圆的有关性质等,但用向量的外积证明比较简捷.

如图2所示,c＝b-a,两边同时叉乘c(注意c要放在等式两边的同一边),所以c×c＝c×(b-a),即0＝c×b-c×a,因此有c×b＝c×a,所以

图2

4.2 平行六面体的体积

如图3所示,b×c垂直于底面,即垂直于b与c所确定的平面,其长度为|b×c|＝|b||c|sinθ,θ为b,c所夹的角,实际上就是底面平行四边形ABCD的面积,因此a·(b×c)＝|a||b×c|cosα,α为b×c与a的夹角,而|a|cosα为平行六面体ABCDA1B1C1D1底边ABCD上的高h,故a·(b×c)表示以a,b,c三个向量为邻边所形成的平行六面体的体积,即空间中不共面的三个向量a,b,c为邻边所形成的平行六面体的体积为|a·(b×c)|(当向量a与向量b×c的夹角为钝角时,其值为负,故要加上绝对值),与坐标系的选取无关.

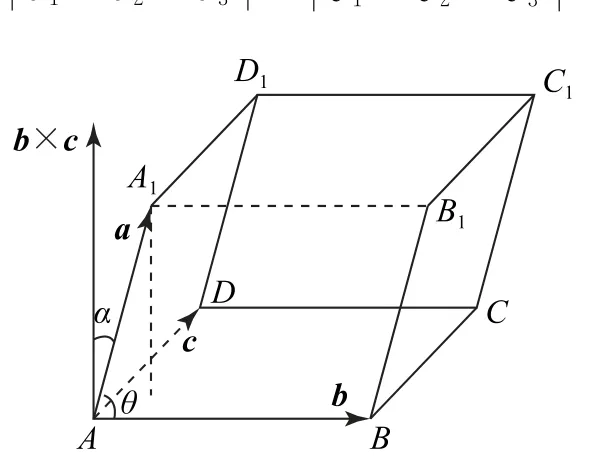
图3

若a＝a1i＋a2j＋a3k,b＝b1i＋b2j＋b3k,c＝c1i＋c2j＋c3k,则有

由行列式的性质可推导出a·(b×c)＝(a×b)·c＝(c×a)·b,a×(b＋c)＝a×b＋a×c等.

4.3 平面方程

在强基计划招生考试或者数学竞赛的有关考题中,经常会遇到求直线和平面的方程、面积、体积的问题,求平面的方程时经常使用公式③,求四面体或者平行六面体的体积时会用到公式②,学习完向量的外积后,可更加全面地了解和理解公式的本质意义.

5 小结

本文介绍了向量外积的定义及其几个性质在中学数学中的应用.向量内积和外积是向量两种不同形式的乘积,且结果不一样,一个结果为数,一个结果为向量.向量的内积表示一个向量在另一个向量上的投影长和向量本身长度的乘积,是一个数.而两个向量的外积则表示与这两个向量垂直(右手法则)、长度为以两个向量为邻边的平行四边形的面积大小的一个向量,向量的两种乘法有本质的区别.

中学数学教材一般都会介绍向量的内积及其应用,没有介绍向量的外积,其实也有一些数学教材介绍了向量的外积及其应用,介绍了矩阵和行列式的知识.通过对向量外积的学习,学生可以更加清楚地理解向量的两种乘法的区别和联系,更加完全地理解向量的本质.特别是通过向量的外积证明有关公式、定理或解题时,程序化的操作带来的方便让学生感受数学的美.