例析平面向量数量积范围的常用求解策略

张 平

(广东省珠海市实验中学)

向量是既有长度又有方向的量,是联系代数与几何的桥梁,数量积既是向量中的一个核心概念,又是一种重要的运算法则与工具.通过平面向量数量积的最值或范围问题,考查学生对知识的整合与灵活应用能力,是近年高考试题的一个热点.此类题目呈现方式简洁,但问题灵活多变,同时解题方法多样,区分度大,因此能充分考查学生的数学学科素养.本文结合具体例题,紧扣平面向量“数”与“形”双重特征,对平面向量数量积范围求解策略进行探究,归纳总结此类问题的常用解法,以期提高分析、解决问题的能力,提升数学素养.

1 数量积的基础知识

1.1 数量积的定义

a·b＝|a||b|cosθ,其中θ(0≤θ≤π)为非零向量a,b的夹角.规定0·a＝0,特别地,a·a＝a2＝|a|2.

1.2 数量积的坐标形式

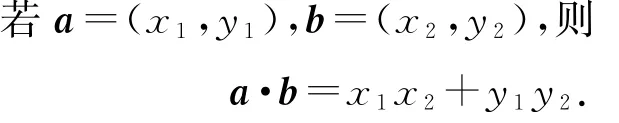
1.3 常用结论

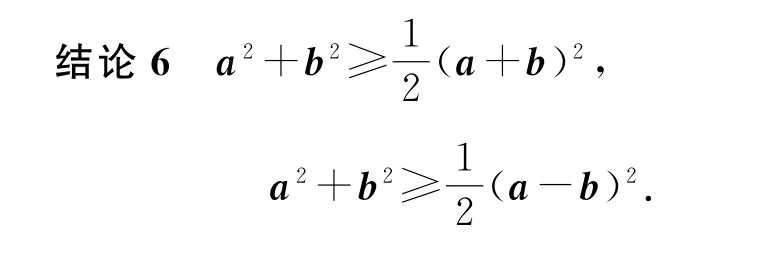
其中结论1～结论3主要用于数量积求解过程中的向量转化或数量积的恒等变形,结论4～结论6主要用于向量数量积的范围或最值的求解.

2 典例分析

图1

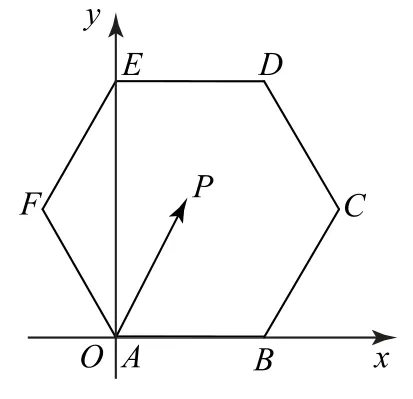
图2

例2 (2012年安徽卷理14)若平面向量a,b满足|2a-b|≤3,则a·b的最小值是_________.

当且仅当向量a＋b与c方向相同时等号成立,故选D.

图3

综上,(a-c)·(b-c)的最小值为1- 2,故选D.

求解本题的关键是对题目信息的合理转化与应用.方法1主要应用了数量积的运算性质与定义;方法2则通过赋予向量坐标,利用判别式法求解;方法3则通过对题目信息的几何化,借助于解三角形知识求解.

A.[-5,3]

B.[-3,5]

C.[-6,4]

D.[-4,6]

方法1 由题意以C为坐标原点建立平面直角坐标系,如图4 所示,则A(3,0),B(0,4).因 为PC＝1,所以点P在以C为圆心,1为半径的圆上运动,设P(cosα,sinα),α∈[0,2π),则

图4

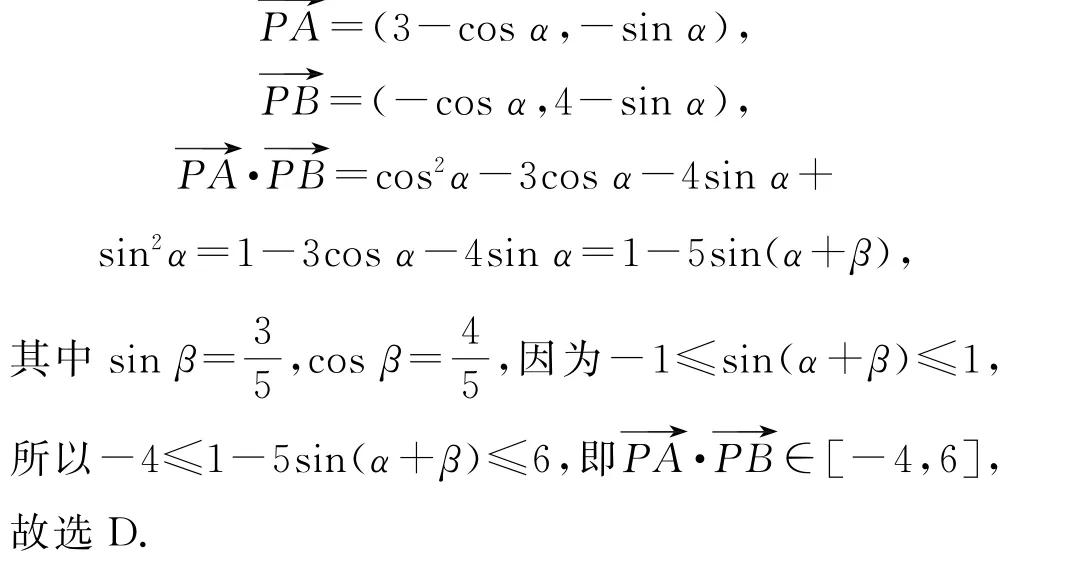
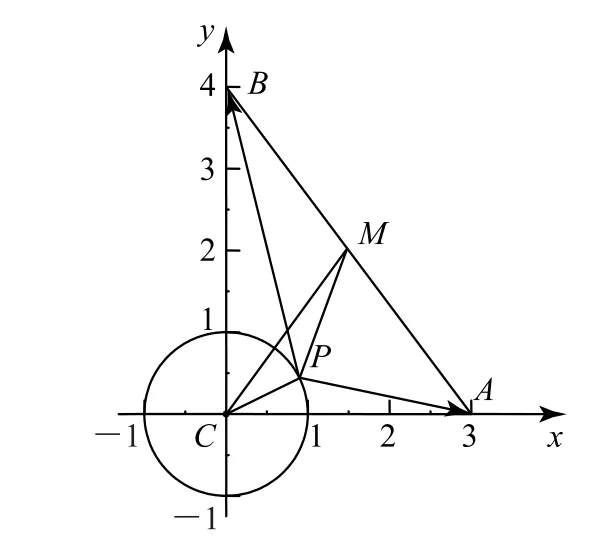
图5

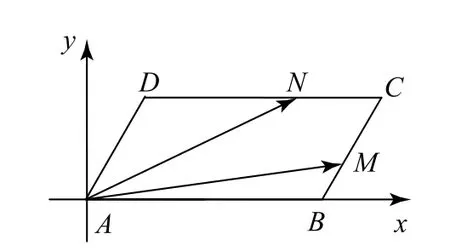
图6

方法2 设M为线段AB的中点,连接CM,方法1 如图7所示,设∠OPA＝α,PA＝x,则

图7

方法2 以圆心O为坐标原点、直线OP为x轴建立平面直角坐标系,如图8所示,则圆O的方程 为x2＋y2＝1,设P(x0,0),A(x1,y1),由对称性知点B(x1,-y1),从而

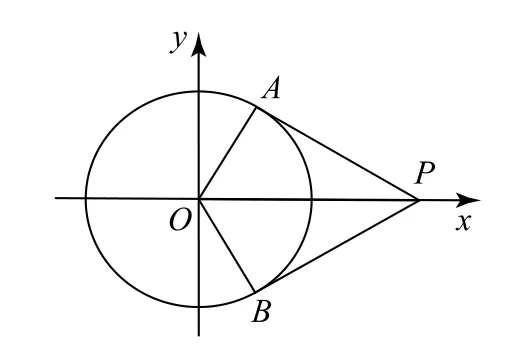
图8

图9

方法1充分利用图形特性,从角入手,利用向量夹角的关系和三角函数知识求解,操作性强;方法2则利用复数与向量间关系,在平面直角坐标系下,借助于复数的几何意义,通过复数运算确定点的坐标,事半功倍,让人眼前一亮.本题还可用极化恒等式、基底法、坐标法求解.

3 策略归纳

通过例题分析可以看出求平面向量数量积的最值或范围通常分为两个环节.首先是将目标数量积进行合理转化,完成建模过程.平面向量数量积的计算有三种基本策略:一是定义法,要求知道相关向量的模与夹角,对转化能力、运算能力和空间想象能力等要求比较高;二是坐标法,要求建立合适的平面直角坐标系,将“形”化“数”,以“数”定“形”;三是极化恒等式,但要求“和向量”或“差向量”的模为定值.因此在这一环节,除了运用向量的线性运算等基础知识外,我们还要结合图形的特点,挖掘图形背后隐藏的信息,以求解问题为中心目标,实现信息提取与整合,通过知识的综合运用、方法的灵活选择实现数量积的“几何化”或“函数化”.其次是“解模”过程,对于“几何化”的数量积,即求解平面几何中的最值或范围问题,主要利用数量积的不等关系、平面图形的几何特性、三角形的相关性质进行判断;对于“函数化”的数量积,则是求解代数中函数的最值与值域、不等式的解集等问题,主要通过三角函数、基本不等式、一元二次方程、二次函数、三角函数、导数等知识解决问题.

向量是代数与几何的交会点,向量的基础知识、常见公式与性质是解题的基础,如平面向量基本定理、数量积、向量极化恒等式、向量柯西不等式等,这些常见的结论需要熟练掌握和灵活应用.对向量题目条件的挖掘和转化是解题的关键和难点,我们要熟知常用的转化策略,熟练掌握常用的最值求解方法,注重基本方法和技能,注重一题多解和一题多变,养成全方位、多角度思考问题的习惯,树立数形结合的意识.我们相信只要同时具备几何意识和代数思想,在面对向量相关问题时,就一定能做到轻车熟路、一往无前.