数学竞赛中四点共圆问题的证明方法例析

扬州大学数学科学学院 (225002) 王洛川 濮安山

四点共圆问题通常通过构造辅助线与相似三角形等知识相结合，寻找边角之间的数量关系，进行转换，得到有效结论，利用对应的证明方法证明四点共圆.本文通过几个典型例题总结分析数学竞赛中四点共圆问题的不同证明方法，供参考.

一、利用三点确定一个圆

首先证明四点中的任意三点共圆，再证明第四个点在圆上.

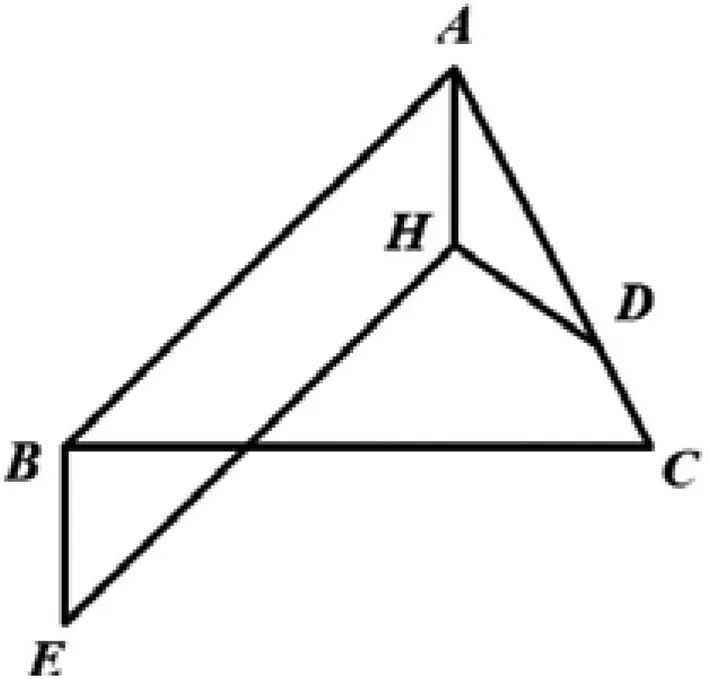
图1

例1 如图1，设H为锐角三角形ABC的垂心，点D在直线AC上，HA=HD，四边形ABEH为平行四边形.证明：B,E,C,D,H五点共圆.

分析：本题虽然是一道证明五点共圆的问题，但是步骤、方法与四点共圆问题相同，可先证明B,C,D,H四点共圆，再证明第五个点E在此圆上，即证五点共圆.

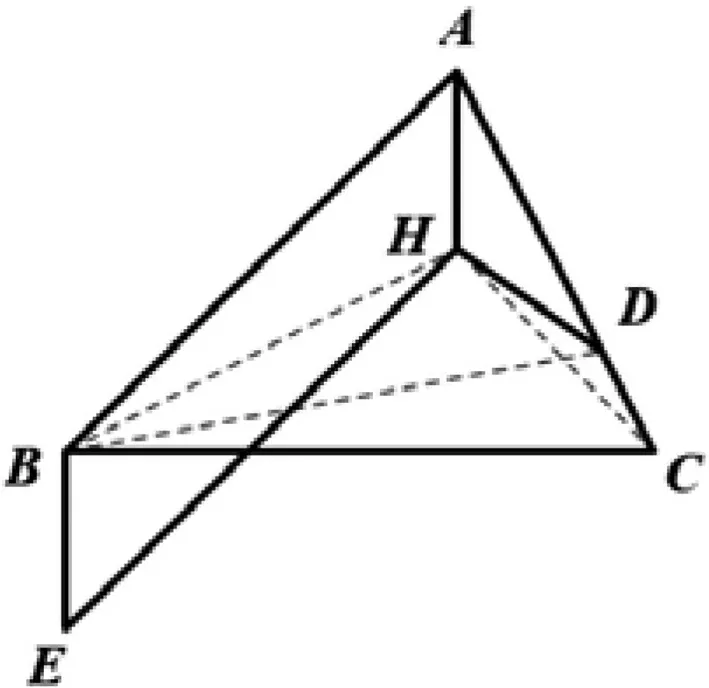
图2

证明：连接BH,HC,BD，如图2.由BH⊥AD,HA=HD，BH为AD的垂直平分线.则∠HBD=∠HBA=90°-∠BAC=∠HCA.从而B,C,D,H四点共圆.再由AH⊥BC,AH∥BE，得BE⊥BC.由HC⊥AB,HE∥AB，得HE⊥HC.点B,E,C,H均在以EC为直径的圆上.所以B,E,C,D,H五点共圆.

二、运用圆上点到圆心的距离相等

如果能证明四个点到某个点距离相等，可以确定这个点是一个圆的圆心，从而四点共圆.

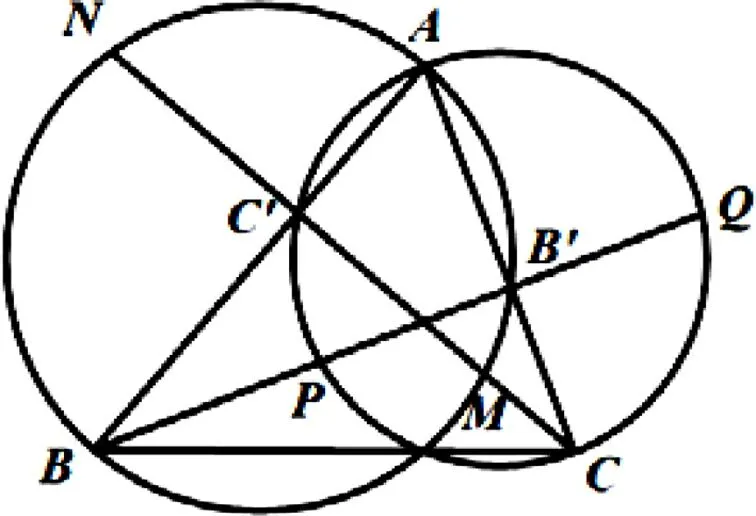
图3

例2 如图3，给定一个锐角△ABC，以AB为直径的圆与AB边上的高线CC′及其延长线交于点M,N，以AC为直径的圆与AC边上的高线BB′及其延长线交于点P,Q.证明：M,N,P,Q四点共圆.

分析：本题利用射影定理和切割线定理，建立等量关系，证明了M,N,P,Q四点到点A的距离相等，则AM，AN,AP，AQ的长度为半径，A为圆心，M,N,P,Q四点共圆.

图4

证明：连接AM,BM，如图4.由于AB,AC是两圆的直径，AB垂直平分MN，AC垂直平分PQ.故AM=AN,AP=AQ.在Rt△ABM中，MC′是斜边上的高，由射影定理得AM2=AC′·AB，同理AP2=AB′·AC.因为∠BC′C=∠BB′C=90°，所以B,C,B′,C′四点共圆，由切割线定理得AC′·AB=AB′·AC，故AM2=AP2，即AM=AP.从而AM=AN=AP=AQ.故M,N,P,Q四点是在以A为圆心的圆上.

三、利用圆的性质：同弧所对的圆周角相等

若将所需证明的点连成共底边的两个三角形，顶角在同侧且相等，则四点共圆.

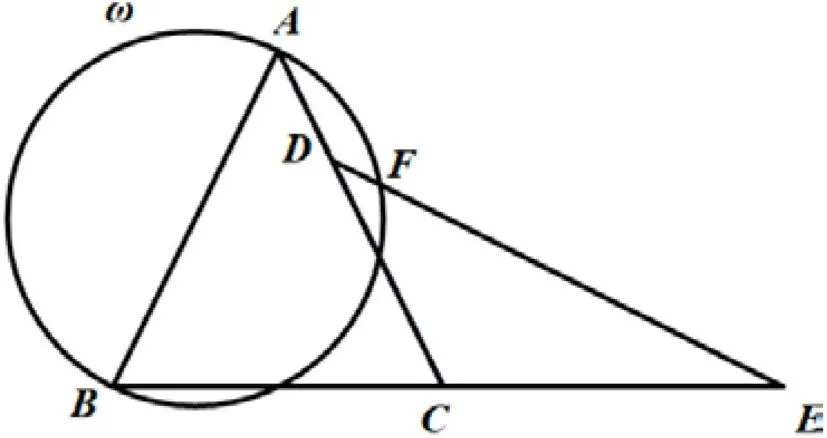
图5

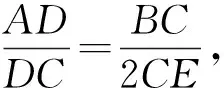
分析：本题通过作辅助线构造平行四边形得到边的关系，利用圆周角的性质对角的关系进行等量变换，从而得到∠CDF=∠CBF，证明四点共圆.

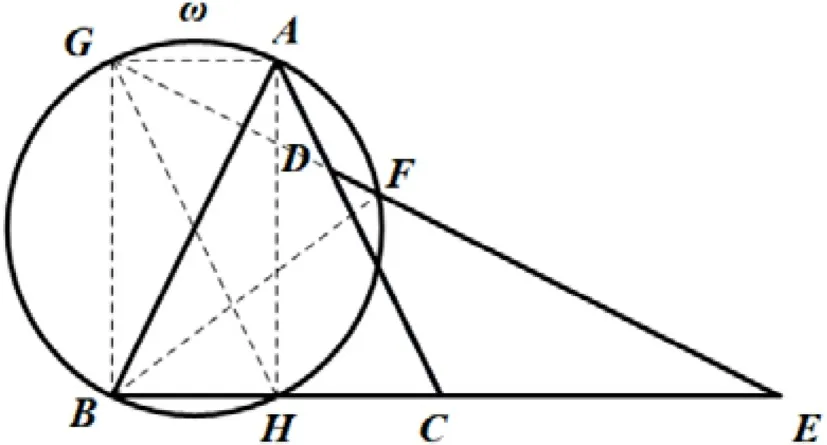
图6

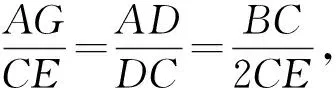
四、利用圆内接四边形性质定理的逆定理

若平面内四点连成的四边形对角互补或者一个外角等于其内对角，则四点共圆.

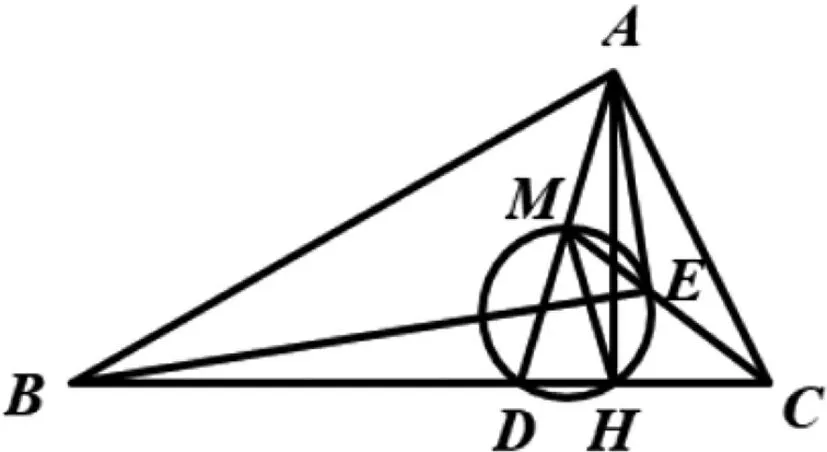
图7

例4 如图7，AD,AH分别是△ABC(其中AB>AC)的角平分线、高线，点M是AD的中点，△MDH的外接圆交CM于点E.求证：∠AEB=90°.

分析：本题通过边角关系证明三角形相似，利用等角的代换证明∠BHE与∠BAE互补，从而证明四点共圆.因为同弧所对的圆周角相等，即证∠AEB=90°.

图8

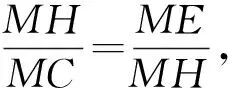
五、利用相交弦的逆定理

相交弦定理的逆定理：把被证四点连成两两相交的线段，若它们各自被交点分成的两线段之积相等，则四点共圆.

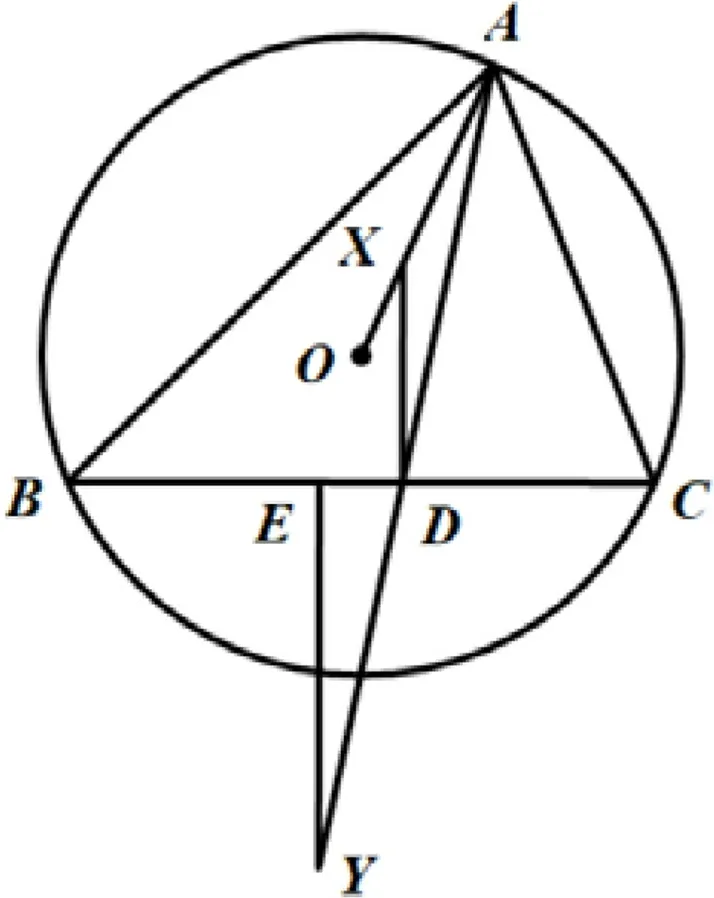
图9

例5 如图9，在△ABC中，已知AB≠AC，O为△ABC的外心，∠BAC的角平分线与BC交于点D，点E与D关于BC的中点对称，作DX⊥BC交AO于X，EY⊥BC交AD的延长线于Y，求证：B,X,C,Y四点共圆.

分析：本题作Y对称点Y′，构造出两条相交弦BC和XY′，将证明B,X,C,Y四点共圆转换为B,X,C,Y′四点共圆.利用圆周角的性质证明X,A,Y′,P四点共圆，再通过相交弦定理和等量代换，得到XD·DY′=BD·DC，证明四点共圆.

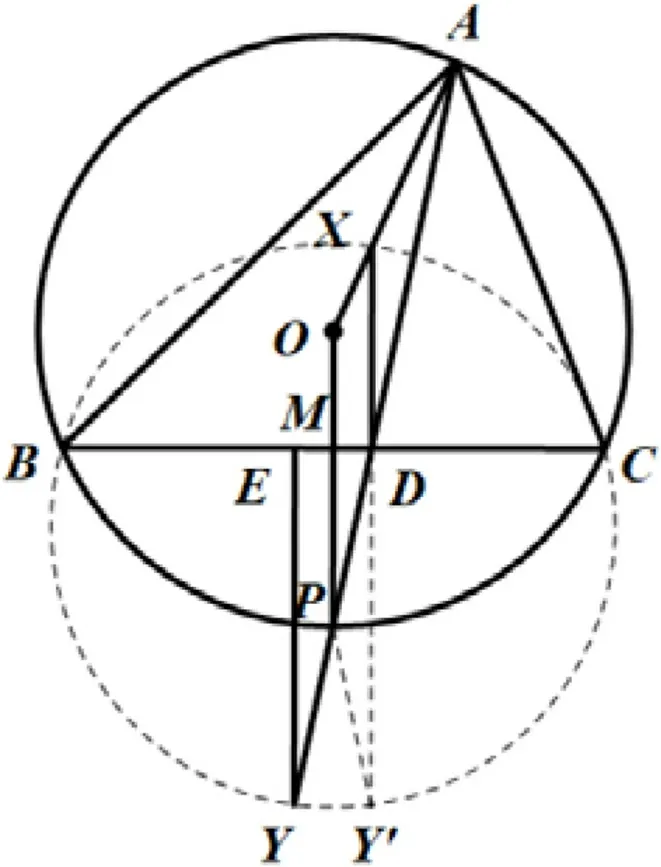
图10

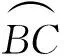
六、利用割线定理的逆定理

将四点两两连接并延长交于一点，若从交点出发至一条线段的两个端点所成线段之积等于从交点出发至另一条线段的两个端点所成线段之积，则四点共圆.

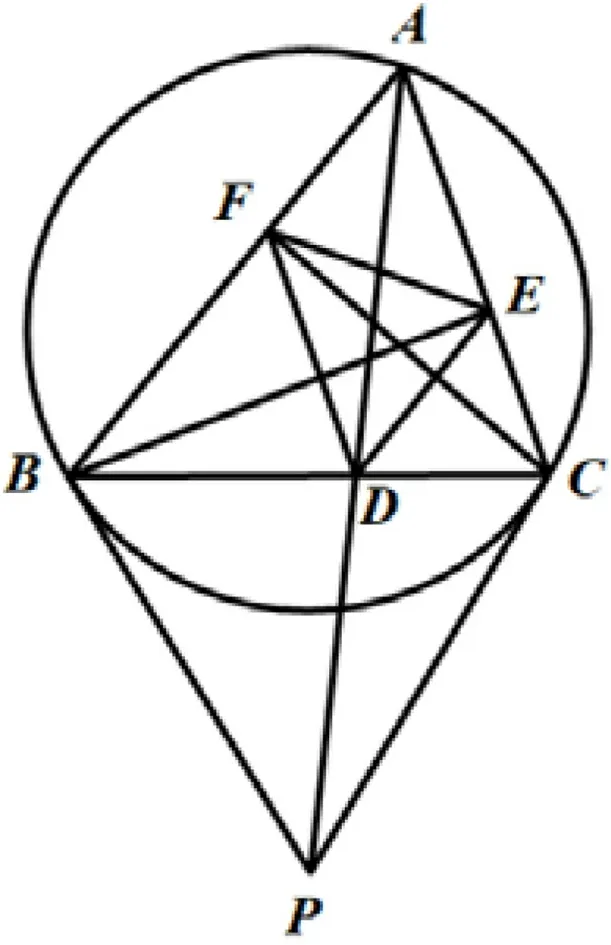
图11

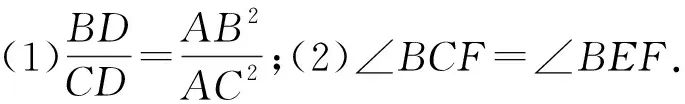
分析：本题的第二问要证∠BCF=∠BEF，这两个角可以看作弦EF所对的圆周角，即证B,C,E,F四点共圆，利用第一问的结论和边的等量关系证明AE·AC=AF·AB，证明四点共圆，得到结论.

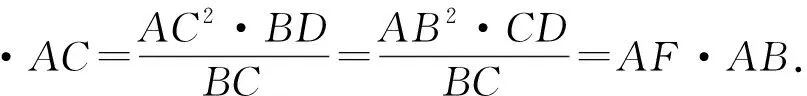
七、利用托勒密定理的逆定理

托勒密定理的逆定理：对于任意一个凸四边形ABCD，总有AB·CD+BC·AD≥AC·BD，等号成立的条件为ABCD四点共圆.利用此定理证明四点共圆通常需要找到边与边的数量关系.

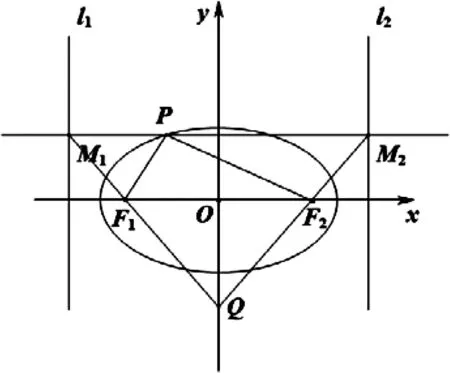
图12

例7 如图12，设椭圆C的两角点为F1,F2，两准线为l1,l2，过椭圆上的一点P，作平行于F1F2的直线，分别交l1,l2于M1,M2，直线MF1与MF2交于点Q，证明：P,F1,Q,F2四点共圆.

分析：本题是椭圆中的四点共圆问题，利用托勒密定理，巧妙地得到所设参量和椭圆离心率的关系等式，再利用椭圆的性质进行带参计算，化简证明等式成立，即证四点共圆.