“二次函数与面积总复习”教学实录与评析*
内江师范学院数学与信息科学学院 (641100) 程雪莲 赵思林四川省成都市石室中学 (610015) 李贤江
1 引言
二次函数与面积综合问题是初三数学总复习教学的重点内容,也是学生总复习和中考的难点.二次函数可以联系一次函数、反比例函数、方程、不等式、平面几何(含距离、角度、面积等)、最优化等知识或实际问题而形成有一定难度的面积综合问题,对学生灵活运用二次函数知识去分析和解决问题有一定帮助.对一堂初三“二次函数与面积总复习”教学观摩课作了实录,并介绍了一线教师和学科专家的评课.
2 课堂实录
让学生回顾已经学过的一次函数、反比例函数、二次函数的图象与性质,引入新课.
例已知二次函数的图象经过三点A(-1,0)、B(0,5),C(2,9).
问题1 求过A、B、C三点的二次函数解析式.
师:我们可以怎样求二次函数的解析式?
生1:设二次函数的解析式为y=ax2+bx+c,然后将A、B、C三点的坐标代入,得到一个三元一次方程组,从而解得a=-1,b=4,c=5.故y=-x2+4x+5.
师:这里用了什么数学方法?
生1:待定系数法.
师:很好.解析式还有其他设法吗?(必要时提示:点B(0,5)的特点)
生2:由抛物线在y轴上的截距是5,所以可设其解析式为y=ax2+bx+5.以下从略.
问题2 求△ABC的面积.
师:求解思路是什么?
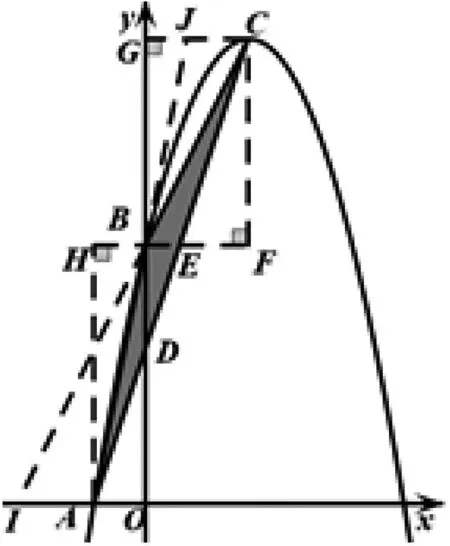
图1
生3:如图1所示,AC与y轴于点D,则S△ABC=S△ABD+S△DBC=BD·(CG+OA)÷2=BD·(|xA|+xC)÷2.因为BD的长度可以通过确定点D的坐标得到,所以可设直线AC的解析式为y=kx+b,将A、C的坐标代入后可求得y=3x+3,则点D的坐标为(0,3),所以BD=|yB-yD|=2,故S△ABC=3.
师:还有没有其他方法?
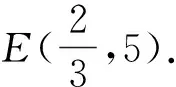
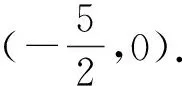
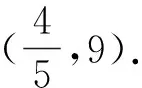
师:非常好.这些方法总是要用到“割”“补”的思想方法,这是处理面积(体积)问题的通性通法.
评析:该问题是一个具有思维价值的问题,能激活学生思维的发散性,有利于培养学生的创新思维.老师的总结很必要、很到位.
问题3 在x轴上是否存在点K,使得B、C、K三点构成的三角形是直角三角形?如果存在,请算出这个三角形的面积;如果不存在,请说明理由.
生7:可以先假设点K存在,并设点K(a,0),再利用勾股定理解答.
师:问题是没有明确哪一个角是直角,因此需要分类讨论.
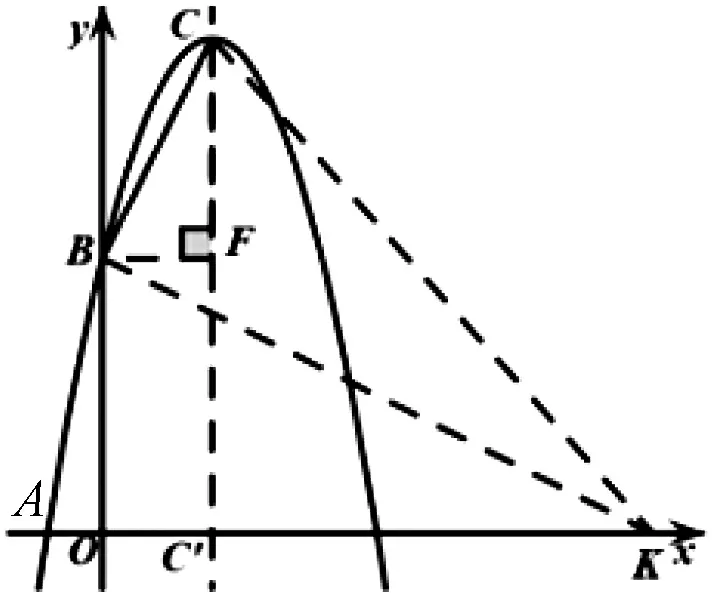
图2
生8:如图2,可以分三种情况,再利用勾股定理:
(1)若∠CBK=90°,
BC2+BK2=CK2;
(2)若∠BCK=90°,
BC2+CK2=BK2;
(3)若∠BKC=90°,BE′2+CK2=BC2.
师:对.现在的问题是,如何用坐标把线段BC、BK、CK的长表示出来?(类比问题2的解答)
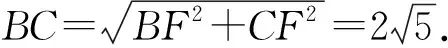
师:很好.解出来的答案是什么?
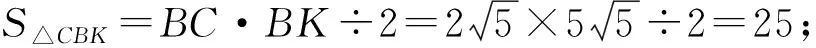
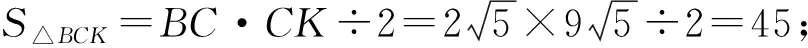
(3)无实数解.
评析:该问题的难处在于,需要先构造直角三角形,再用勾股定理,最后用坐标表示出两点之间的距离.
问题4 设抛物线与x轴的另一个交点为L,点Q在抛物线上且在直线BL上方.在对称轴上是否存在一点P,使得以B、L、P、Q为顶点构成一个平行四边形?如果存在,请求点P、Q的坐标,并求该平行四边形的面积;如果不存在,请说明理由.
生9:不存在.因为当BL∥PQ且BL=PQ时,四边形BLQP才是平行四边形.而点P在对称轴上,点Q抛物线上且在直线BL上方.因此,从图形观察可知,同时满足BL∥PQ且BL=PQ的情况不存在.
师:在这种情况下P、Q的确不存在.但还有没有其他可能的情况?比如,BL不是平行四边形的一边.
生10:当BL是BPLQ的对角线时,就有可能了.设P(2,m),Q(n,-n2+4n+5),可用平行四边形的对角线互相平分的性质解决.
图3
.
E
F
.
生11:观察发现,E′F′中点坐标是1.
师:还有没有其他方法?
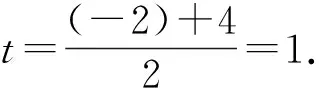
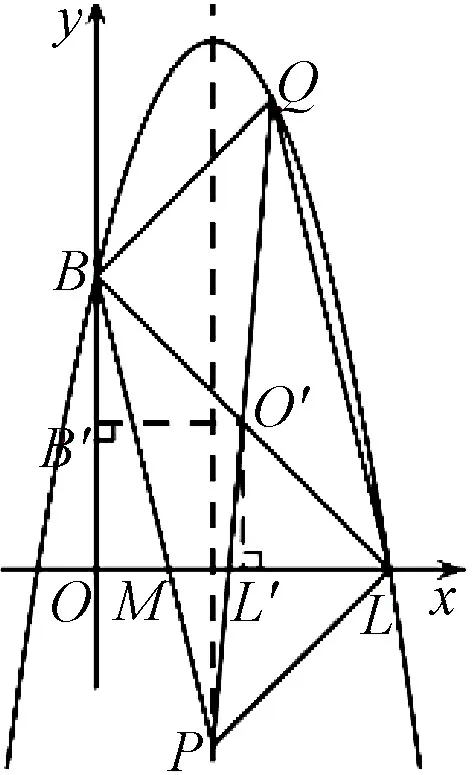
图4
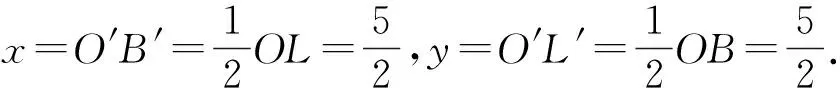
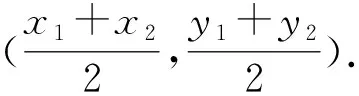
现在如何由中点O′的坐标来求点P、Q的坐标?
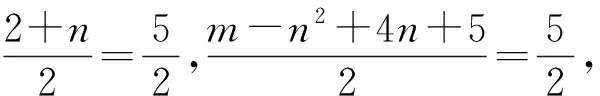
师:对.怎样求平行四边形的面积?
生11:可以以BP为底边,过点L向BP作垂线,从而得到BP边的高,不过高的长度不知道怎么求.
师:这个思路比较自然,但高就是点到直线的距离,我们现在还不容易求出来.这时需要同学们另外想办法方法.比如,可否尝试用问题2的思路即“割补”的方法解决呢?
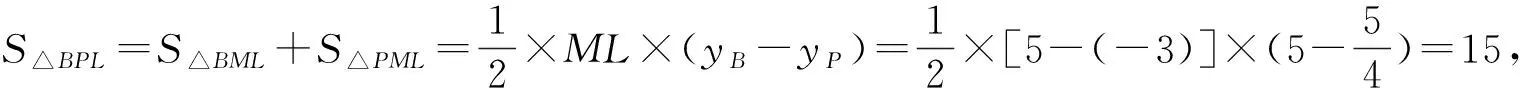
师:对.这里我们再次体会到“割补”方法的巧妙.还需注意在分析时要善于分类讨论,并做到不重不漏.
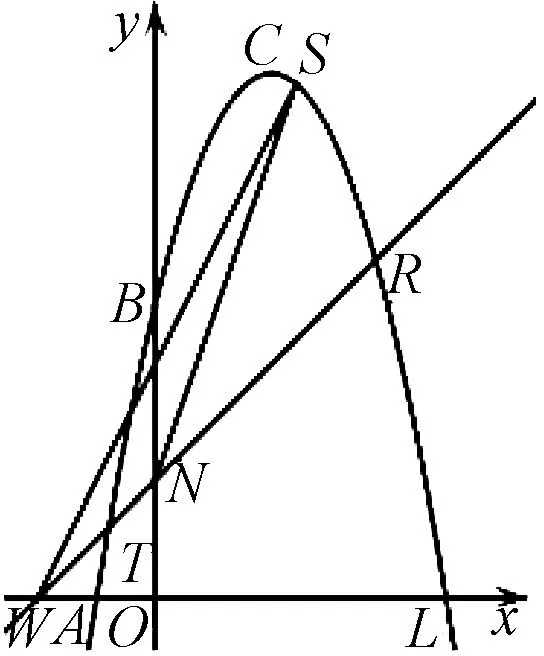
图5
问题5 如图5,一次函数y=x+2的图象与抛物线交于T、R点,与x轴交于点W,与y轴交于点N.设点S是抛物线弧BR上的一点(不与B、R点重合),设其横坐标为m,当m取何值时△WNS的面积取得最大值?并求出最大值.
师:这个最值问题怎样解决?
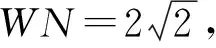
师:这思路很好.但WN边上高用什么方法求呢?
生14:没有.
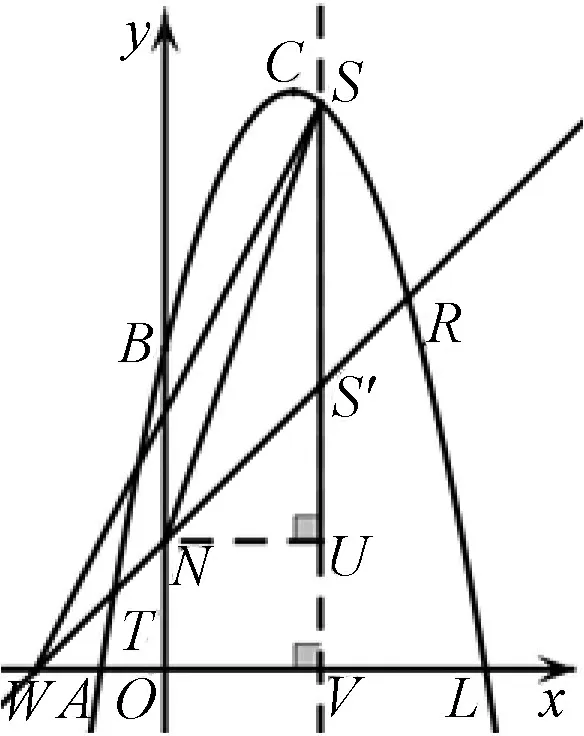
图6
生15:如图6,可以过点S向x轴作垂线交直线TR于点S′,交x轴于点V,其中S′(m,m+2),利用S△WNS=S△WSS′-S△NSS′可以求得.
师:△WSS′和△NSS′的面积如何求?
生15:以SS′为底,再找到△WSS′和△NSS′在SS′上的高即可.
师:如何找到SS′上的高?是否可以构造直角三角形?
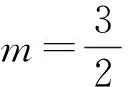
师:这个题目虽较难,但只要善于采用“构造(直角三角形)”“数形结合”“割补”“面积变换”等思想方法,问题就会迎刃而解.因此,“构造”“割补”“数形结合”“面积变换”是解决二次函数与面积综合问题的几个关键词.
师:本课运用了哪些数学方法?运用了哪些数学思想?
生16:本课运用了观察法、待定系数法、割补法、假设法、反证法等数学基本方法,还用了数学结合、函数与方程、化归与转化、分类讨论等数学思想.
评析:归纳总结有利于开发元认知,有利于学生建构知识网络,提炼数学思想方法,促进数学思维的发展.
3 教学评价
初三复习课应以问题串为载体,体现问题性、综合性、探究性和衔接性.本课师生从问题出发,重视“四能”的培养,师生互动比较充分,学生思维活跃,是一堂成功的探究型复习课.一线教师和学科专家普遍认为本课具有以下特点:
问题性:基于“问题是数学的心脏,问题是教学的心脏,问题是学生学习的心脏[1]”和“问题是思维的土壤”,本课围绕“二次函数和面积”设置问题串,体现了“为问题而教”“为问题而学”“为问题解决而教”“为问题解决而学”的教学理念.问题串的解决需依托数学的核心知识和思想方法,问题之间层层递进,让学生思维经历“由浅到深”“由单一到发散”“由固定到开放”等思维过程.
综合性:综合性问题是学生发展“四能”和核心素养的重要载体.本课帮助学生比较系统地复习了一次函数和二次函数的性质、三角形、平行四边形等基础知识,学习了待定系数法、观察法、割补法、反证法等数学基本方法,运用和领会了数形结合、分类讨论、化归与转化、割补转化等数学思想.5个新颖的典型问题,对学生而言是没有做过的,问题的难度逐步加大,具有较好的区分度,能够使不同层次的学生在问题分析、问题探究与问题解决过程中得到不同的发展.综合情境才能培养学生的数学素养,发展学生的数学思维能力.
探究性:本课注重通过引导学生对一个个问题“抽丝剥茧”,探究如何构造垂线、构造直角三角形,灵活运用分割法求三角形、平行四边形的面积.问题2通过构造三角形,解决面积问题;问题3本身是一个非常典型的探究性问题,通过构造直角三角形、利用勾股定理,用坐标表示两点之间的距离;问题4意在引导学生初步学会探究线段的中点坐标公式;问题5是一个需要构造二次函数,并探究其最值的问题.
衔接性:培养学生的持续学习能力是初中数学教学的重要任务.本课探索的两点之间的距离公式、线段的中点坐标公式,既培养学生的全脑思维有好处(因为这两个公式的发现,需要学生直观的几何思维(右脑)与精确的代数思维(左脑)的结合与转换),又有利于学生为高中数学学习打下良好基础.
需要说明的是,本课存在容量大、难度高的问题.本课适合安排2课时.问题3和问题4都有与高中解析几何接轨的意图,这是很好的,但要控制难度和运算量,否则让学生吃“夹生饭”就得不偿失了.这种初三复习综合课的设计与实施,需要教师提升MPCK素养和教研创新素养[2].

