“以寻找思路为核心”的解题教学——以一道2021年上海中考题的教学为例

江苏省如东县马塘初级中学 (226400) 王 陈

涂荣豹教授在文[1]中提到：教学生学会思考就是教“解题思路是怎样想到的”，也就是说要“让学生自己想到”.但是，解题思路的教学一直是数学解题教学的难题.本文就一道2021年上海中考题为例，谈谈解题教学的设计及其思考.

一、求解思路

考题(2021年上海中考题)如图1，在四边形ABCD中，AD∥BC，∠ABC=90°，AD=CD，O是对角线AC的中点，联结BO并延长交边CD或边AD于点E.

(2)若DE=2，OE=3，求CD的长.

图1

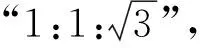
(2)由于点E的位置并没有明确，所以需要分类讨论，比如点E在AD上或点E在CD上.

情形1：如图2，当点E在AD上时，可先证出四边形ABCE是矩形.设AD=CD=x，在Rt△ACE和Rt△DCE中，将CE“算两次”，即CE2=AC2-AE2，CE2=CD2-DE2，可得62-(x-2)2=x2-22，解得x=1或x=1(舍去).故CD=1.

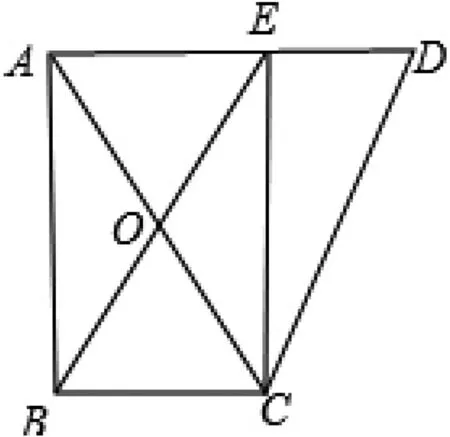
图2

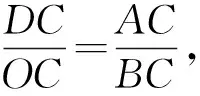
二、解题教学微设计

教学环节一 基础热身

出示“考题”，预设以下问题启发学生自主寻找“考题”第(1)①、②问的思路.

问题1：△DAC与△OBC形状有什么特殊？你是从题目中哪些条件解读出来的？

问题2：图1中，与∠DAC相等的角有哪些，用一个记号把它们都标注出来；

问题3：若BE⊥CD，△BEC成为一个直角三角形了，它会是一个特殊的直角三角形形吗？

问题4：“破译”出图形中有多个30°的锐角之后，待分析的值，你们有哪些好的思路呢？你能直接看出△ADC的三边之比吗？

教学环节二 拾级而上

预设以下问题，启发学生自主攻克“考题”第(2)问的第1种情形“点E在AD上”.

问题5：再读一下“题干”，点E有没有明确在四边形ABCD的哪条边上？在开始处理第(2)问时，你觉得首先要怎样去思考？(预设学生要想到分类讨论，考虑点E在不同的边上)

问题6：当点E在边AD上时，你觉得本题的图形该如何构造？有哪些特殊的地方呢？比如四边形ABCE是否比较特殊？

问题7：如图2，在△ACD中，CE可看成该三角形高，这个三角形中有哪些线段的长是确定的？还有哪些边长之间具有等量关系？该如何求△ACD的边长CD呢？

问题8：“算两次”是种重要的解题方法，在本题中，你体会到“算两次”方法的价值了吗？

教学环节三 攻克难点

问题9：当点E在CD上时，图形仍然可以用图1进行分析，除了第(1)①问已证过的两个三角形相似(△DAC∽△OBC)之外，本图中还有哪些三角形也能相似吗？(预设：△EOC∽△ECB)

问题10：上面两组三角形相似能带来哪些对应边成比例，将它们书写、对齐，研究一下，这些对应边中共有几个未知量，能否用较少的未知数来表示它们？

图3

问题11：设AD=CD=x，再设OB=OC=m，试用含x，m的式子，表示出两组相似三角形的相应对应边的比例式，整理一下，看看有什么进展？是否消去m得到关于x的方程？

问题12：另解思考，如图3，延长BE，AD交于点F，能否用含x的式子表示EF？从而运用△DEF∽△CEB列出关于x的方程.

教学环节四 解后回顾

小结问题1：本题求解过程中，你觉哪一个步骤是最关键的，请说说你的理解；

小结问题2：反观解题过程中，遇到了不少基本图形、特殊图形，你觉得这些基本图形的哪些性质对解题是有较大帮助的？

小结问题3：有同学针对第(2)问总是容易漏解，你有什么好的建议给他说说吗？

小结问题4：继续探究“考题”最后一问，点E在边CD上时，有没有其他的方法？(预设两种辅助线构造方法，如图4，连接DO并延长交BC于F，过点F作FG∥BE交CD于点G；或者如图5，作AF∥BE交CD的延长线于点F，供同学们课后继续探究)

图4

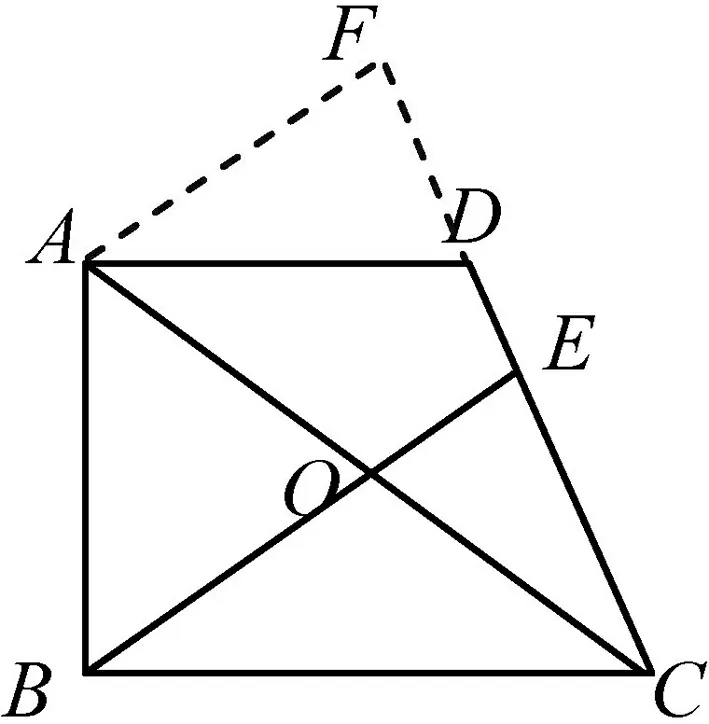
图5

三、解题教学的一些思考

(1)精心预设教学引导语，让学生自己想到解法

如涂荣豹教授指出的，解题教学要“以寻找思路为核心”，特别是解题教学的重点不是“解题”而是“学解题”.学生往往特别关注解题结果，而“学解题”的关键是解题方法或思路是如何发生、找到、接通的.所以在本文“考题”的教学微设计中，我们注重给出了针对每个小问的教学引导语，以问题驱动教学进程，让学生能在这些启性用语的帮助下，自己想到解法.这样学生不仅解决了问题，而且收获了解题方法和解题自信.特别是，经常安排这样的启发式教学，学生在以后独立遇到陌生问题的探究时，就可以联想到老师是如何启发自己理解题意、获得思路.长此以往，学生会在“春风化雨、润物无声”中提升解题能力.

(2)重视解题回顾与反思，让学生想清关键步骤

解题教学的最后环节要安排回顾与反思，精心预设一些小结问题，带领学生围绕本课所学进行回顾反思，特别是可以针对解题进程中的关键步骤进行回顾，考虑到不同层次学生对解题全过程中的关键步骤的理解可能会有差异，这时可安排学生小组内先交流，然后再全班汇报.另外，课堂上因为教学时间所限，若针对某个问题的“一题多解”没有能充分展开，可以作为小结时提出其他解法的一些思路或辅助线构造，安排学有余力的学生课后继续钻研.

(3)开展“一题一课”教学，让学生“长时间思考”

围绕一道典型考题安排一节课进行专题教学是目前老师践行“一题一课”成功经验，实践表明，这类课型可以促进学生围绕某个经典问题进行“长时间思考”，从“快思”走向“慢想”的效果是对这类问题更具深刻的理解，也就能更好地践行“学深、悟透、学活”的教学目标.