例谈在小学数学教学中运用验证法培养学生实证精神

江成刚

(苏州市吴江区盛泽实验小学，江苏苏州，215228)

验证是指对研究对象有一定程度的了解和认识后，提出某种假设，为证明或检验这种认识或假设是否正确而进行的一种探索性活动.验证在数学发展和数学教学中的作用非常大，数学中的许多结论、定律、公式都来源于猜想，然后经过验证，猜想得到证实后就变成结论、定律、公式进入数学体系之中.

教学中学生通过验证不仅要掌握知识、理解结论、运用结论，更重要的是在验证中发展学生的探究能力和学习能力，同时，培养学生的实证精神和严谨的求学态度.

典型案例重现

验证法在教学中深受老师们的青睐.但在小学数学教学中，存在一些不规范的验证，如下面两个案例.

案例1在学习圆的周长时，老师让学生实际操作验证圆的周长与半径之比，一些学生不实际测量计算，而是自己设计几个数字，使比值近似于3.14，甚至有学生直接让所有比值全部等于3.14，这些学生显然是预习了教材，知道了结论后的投机取巧.这部分学生甚至会嘲笑老老实实地测量计算的同学，笑话他们的“笨拙”和“不知变通”，但实际上，在学习上更需要这样的“笨拙”.

案例2对乘法交换律的举例验证.很多学生在不到一分钟的时间里写出了二十几个算式，而且其中的很多还是像123×652=652×123这样计算比较复杂的算式，很显然他们不会在这么短的时间内计算出结果来，那么只能说明他们并没有实际计算而是通过乘法交换律的结论直接写出来的.通过交流证实，确实是这样写出的.

师：这么短的时间内你怎么写了这么多？

生：其实很简单，随便写两个数字，再换一下位置就可以了.

师：但老师要求计算两个因数的位置交换后的乘积，你没计算怎么知道它们相等？

生：肯定相等，二年级的时候就知道三五一十五，五三也是一十五.

生：乘法交换律就是交换位置后积不变.

这种验证方法显然是错误的，它不是对猜想的验证，而是对结论的直接运用.像这样的假验证成为了课堂的一种形式，仅仅是为了完成课堂预设而走的过程，对学生质疑能力、实证精神、探究能力的培养并无益处.学生没有通过计算来验证自己的假设，而是通过以前的学习经验和乘法交换律的结论直接写出算式来.这也是学生假验证的两个直接原因，一是出于经验、直觉觉得事实就是如此；二是通过预习直接接受了书上的结论，然后再直接运用，当然，假验证的深层原因是缺少质疑和实证精神.

那么在教学中应该如何引导学生学会正确验证，从而助力学生培养起质疑能力和实证精神呢？通过实践证明应该做到以下几点.

2 研究教材，做到心中有数

小学教材中需要验证的内容有很多，那么老师应该对整个教材做一个全面细致的分析和挖掘，把这部分内容整理出来，自己先做到心中有数.

以人教版数学教材为例，小学阶段需要验证的内容如下(表1).

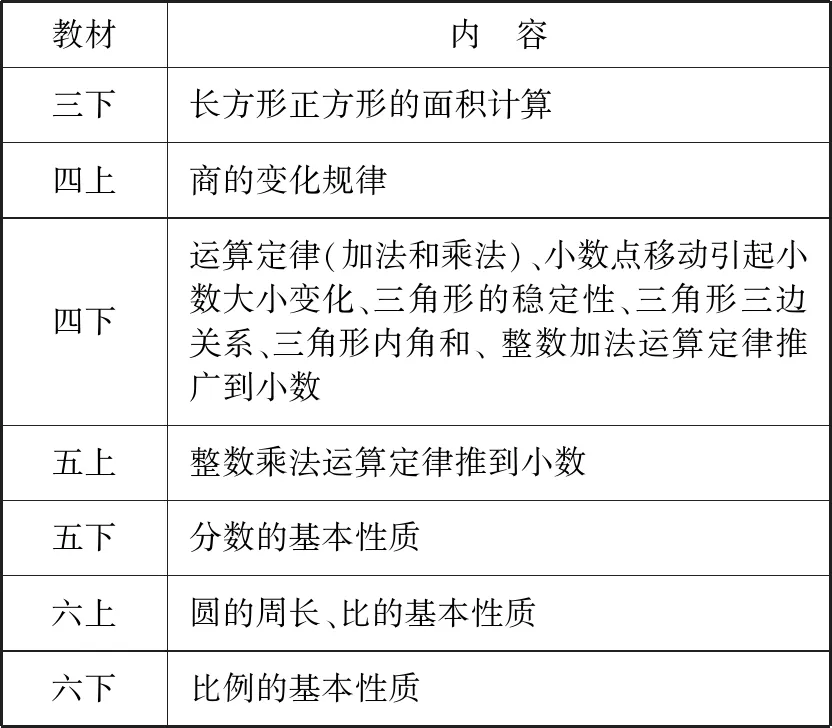
表1

通过研究教材看出，在学段上，需要学生进行验证的知识主要分布在第二学段，这是因为第一学段学生思维发展和知识储备还不够，不具备验证的能力，到了第二学段学生已经有了一定的知识积累和思维能力，有了验证的能力基础；在内容上，验证一般是对一些定律、公式等结论性比较强的知识.这部分知识的获得更需要学生实践探索和质疑验证，以便让学生充分经历获得知识的过程，这样学生对结论的理解才会深刻透彻，避免了学生对结论的机械记忆.

通过系统分析教材，老师对小学阶段的验证内容有一个整体把握，才能根据不同年级和不同内容进行有效的教学设计，使这部分内容前后呼应，形成体系，做到前有引导，中有放手，后有提升.

前有引导，就是在学生刚接触验证时，如三年级下册，长方形正方形的面积计算时，老师要为学生提供可视化的方法示范和指导，先让学生自己模仿验证，而且要有比较详细的说明和步骤，保证学生自己能进行验证实践，积累经验，形成验证的方法.

中有放手，就是指学生有了一定的验证经验，老师就要放手，鼓励学生自己验证，充分经历验证过程，在验证中发现问题，再进行纠正，让学生在验证中感受验证方法的重要性，并养成老实验证的习惯.

后有提升，就是指在高年级段要让学生对以前的验证有回顾、比较、总结.如在六年级下册学习比的基本性质时，老师可以引导学生把商的变化规律和分数的基本性质，放在一起进行比较，并总结出相互之间的关系.在必要阶段还可以以专题的形式，把学过的内容串在一起，使学生比较宏观地了解和看待验证的作用和意义.

3 掌握方法，促进正确验证

3.1 理解验证的意义

许多老师遇到学生假验证的情况会硬性要求学生重新验证，但这种情况下，学生并不会理解验证的意义，心底里觉得是多余的，因此要引导学生明白验证的意义，学生才会主动验证.

从建构主义观点看，学生知识的获得是一个主动建构的过程，需要学生自主经历，从而改组原有经验与知识结构，这就要求学生必须主动进行质疑验证，自己发现自己信服，自己理解自己悟得.

从学习意义和三维目标看，学习不仅要习得知识、掌握方法，更要发展情感和精神.不去质疑验证学习，也能记住知识结论，学生照样可以直接运用结论，解决问题，也会取得高分，但对学生质疑精神却没有任何帮助.没有质疑和求证就无条件地接受知识，只能做知识的搬运工.验证过程就是质疑过程，因此，验证意义更在于对一个人精神态度的塑造和培养.

3.2 验证要老实

像上面的假验证要在教学中避免，学生必须亲自老老实实地验证，重实践重证据，不怕慢不投机取巧.如验证乘法交换律时，学生应该对自己列举的算式逐一计算，然后在看结果是否相同，不能随意书写一些算式，做样子.

3.3 过程要完整

3.4 注重推理

在验证阶段学生往往追求列举尽量多的例子，其实这没有必要，验证不一定要有太多的例子.例子可以不多，但应该伴以推理，通过对有限的例子进行推理论证，达到充分的意义理解，这样才能推而广之，真正在达到验证的目的.如验证分数的基本性质时，可以唤起学生的经验，结合学生的旧知做出推理.学生已经学习了商不变的规律，那么就可以做出这样的推理，在除法中对被除数和除数同时乘以或除以一个相同的数(0除外)，商的大小不变，而分数的分子相当于被除数，分母相当于除数，那么给分子和分母同时乘以或除以一个相同的数(0除外)分数的大小也不变.

这样在验证中结合推理，沟通知识间的联系，促进学生意义理解，更好地掌握知识本质.

4 培养习惯和精神，助力学生成才

学生的实证精神应该从小就培养，要让学生养成多问几个为什么的习惯，规律果真如此吗？这是真的吗？可以怎样证明它？只有学生从小养成这种习惯，才真正有益于学生的学习和成长.

一句很著名的话说，教育就是忘记所学之后剩下的东西.只有习惯和精神是不能忘记的，一旦养成就会终身受益.但现在学生的质疑能力和实证精神还没有很好地发展起来，就像一位同学在验证分数的基本性时说的：“书上说的肯定正确，还验证什么？如果不正确能往书上写吗？”这正反映了学生缺少质疑与实证精神.

学生如果没有质疑意识，对教材内容不敢质疑，不愿质疑，只是无条件地接受遵从，那么学生将养成盲从的习惯.也许在小学阶段这样的学生通过训练也可以顺利地解题，得到高分，但长此以往，对学生的人格成长、学习能力、创新精神的损坏将是巨大的.这样的学生将来会是一个优秀的执行者和追随者，但不会是一个创新者和引领者.

所以，让学生正确验证的核心目的是要培养学生的质疑能力和实证精神.敢于质疑、勇于实证，当养成了这种心性，教育的意义和价值才真正种植在学生心中，“钱学森之问”自然也就解开了.