基于“四个理解”视角下的初中数学作业设计

张群伟

(伊宁市教育教学研究室，新疆伊宁，835099)

章建跃博士提出数学教学是基于理解数学，理解教学，理解学生，理解技术进行的思维与实践活动.作业设计是教学中的必要环节，是课堂教学活动的延伸与补充，同样遵循以上原则.

1 理解数学是设计高品质作业的前提

理解数学，从整体上把握数学结构，才能设计出目标清晰，内涵丰富的作业.只有题目有了准确的定位，具备承载学生发展的功能，才能设计出“少而精”的作业，实现针对性的训练，从而减轻学生的作业负担.

(1) 9；(2) 5；(3) 2.5；(4) 0.25；(5) 0.

该题是学习“二次根式(1)”后的作业之一.《义务教育数学课程标准(2011年版)》对二次根式的要求是“了解二次根式、最简二次根式的概念，了解二次根式(根号下仅限于数)加、减、除运算法则，会用它们进行简单的四则运算”，具体到本课时的教学目标，即为“根据算术平方根的意义了解二次根式的概念，知道被开方数必须是非负数的理由；能用二次根式表示实际问题中的数量关系”.本题是二次根式的简单变形，这种变形在实数范围内的因式分解中有用，也为后继的一元二次方程的解法提供知识支撑.

作业设计要重视对教学内容的整体分析，不仅要体现知识点的反馈，也要关注知识点之间的联系，帮助学生建立能体现学科本质、对未来学习有支撑意义的结构化的数学认知体系.

2 理解学生是设计高品质作业的关键

作业的设计要理解学生，关注学生的思维最近发展区.没有针对性的作业，只会增加学生的学业负担.所以因材施教，设计分层作业，满足不同层次学生的需求，才能使作业真正发挥巩固知识、深化知识、发展能力的作用.

例如，在新授课“多项式的因式分解(1)”后，笔者设计这样一组作业：

A层：

(1) 下列各式从左到右的变形中，属于因式分解的是( )

A. 6x2y=2x·3xy

B.x3-2xy=x(x2-2y)

C. (a+3)(a-3)=a2-9

D.x2+4x+1=x(x+4)+1

(2) 多项式9a2b-3ab2的公因式是.

(3) 若ab=7，a+b=6，则a2b+ab2的值为.

(提示：将多项式a2b+ab2分解因式，你发现了什么？)

(4) 把下列各式分解因式：

① 18a2b-8b；②m2n+mn；③ 2x2-12xy2+8xy3；④ 3x2(x-y)+6x(y-x).

(5) 利用分解因式方法计算：

① 1012-101；② 27×19.99+72×19.99+19.99.

B层：

(1) 下列因式分解正确的个数是( )

①x2-2x+1=(x-1)2；②x2-1=(x-1)(x+1)；③x2-2x=x(x-1)；④ 2x2-2x=2x(x-1).

A. 1个 B. 2个 C. 3个 D. 4个

(2) 多项式3ma3+6ma2-12ma的公因式是.

(3) 边长为a、b的长方形，它的周长为12，面积为7，则a2b+ab2的值为.

(4) 把下列各式分解因式：

① -8a2b+12ab2-4a3b3；

② -24x2y-12xy2-28y3；

③ 2m(m-n)2-8m2(n-m)；

④ (x-y)2-x+y.

(5) 利用分解因式方法计算：

C层：

阅读理解：把多项式am+an+bm+bn分解因式.

解法一：am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b)；

解法二：am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(m+n)(a+b).

观察上述因式分解的过程，回答下列问题：

(1) 分解因式：m2x-3m+mnx-3n；

(2) 已知：a，b，c为△ABC的三边，且a3-a2b+5ac-5bc=0，试判断△ABC的形状.

A、B层的作业设计都是5道题，题型一致，不同层次学生作业时长大体相当，分层后针对性强，能满足部分学生学习需求.逐一比对，第一题问法由“属于因式分解的是”到“下列因式分解正确的个数是”，问题从封闭走向开放.第二题在多项式的项上有变化，结构变复杂，能力要求也相应提高.第三题问题呈现方式不同，A层是直接呈现代数形式ab=7，a+b=6，且有提示：将多项式a2b+ab2分解因式，你发现了什么？B层则利用几何形式，把ab=7用长方形的面积为7，a+b=6用长方形的周长为12来表述，考查学生转化的能力，培养学生的探索精神.四、五两题在难度上也有明显提升.C层的作业是拓展拔高，充分发挥作业作为课堂延伸的功能，用阅读题的形式让学生关注知识学习的过程，学会用数学知识解决实际问题，感受数学的用处.

作业布置切忌随意性、盲目性和一刀切的现象.“不同的人在数学上得到不同的发展”的理念在作业设计上的体现就是重视个体差异，关注学生可持续发展.

3 理解教学是设计高品质作业的保障

《义务教育数学课程标准(2011年版)》指出：在教学中教师要引导学生在真实情境中发现问题和提出问题，利用观察、猜测、实验、计算、推理、验证、直观想象等方法分析问题和解决问题.在作业的设计上结合生活中的现象，让学生学会思考.

例如，在“代数式”的复习课后笔者选择了下面问题：

当你记不住九九乘法表中乘9的口诀时，你可以进行如下的操作：

例如，伸出两只手，做运算4×9时，如图1，从左手开始数4下，数到第4根手指向下弯.这时，该手指左边有3根手指，右边有6根手指，可得36，即4×9=36.

图1

类似的，做运算8×9时，从左手开始数8下，数到第8根手指向下弯.这时，该手指左边有7根手指，右边有2根手指，可得72，即8×9=72.

……

将问题一般化，我们可以解决9n(1≤n≤9，且n为整数)的问题.从左手开始数n下，数到第n根手指向下弯.这时，该手指左边有根手指，右边有根手指.

列式计算说明上述操作的理由.(不能1～9逐个代入)

本次作业让学生从身边熟悉的现象中发现问题，用已有的数学知识去解决问题，考查规律性问题的解决，找到规律并进行验证是解题关键.由此引发思考，乘8的口诀是否有这样的规律？

只有作业联系生活实际，学生感受到数学有用，才能够以数学的眼光观察世界、以数学的思维分析世界、以数学的语言表达世界.

4 理解技术助力高品质作业的设计

合理利用现代信息技术，可以提升学生的探究热情，开阔学生的视野，激发学生的想象力，提高学生的信息素养.技术的应用在预习作业的设计上更有优势，可以化抽象为直观，发现不变的数学本质.

例如，在“圆周角(1)”课前，笔者让学生利用GeoGebra对进行预习.

学生通过软件，可以量出⊙O中AB所对的圆周角∠ACB和圆心角∠AOB的度数，改变C的位置观察两者度数的变化，得到不变的结论：∠AOB=2∠ACB.学生观察图3，利用已有的知识经验，可知∠AOB=2∠ACB，若点C在⊙O上，一般化(图2和图4)的证明，又如何完成？对于初三学生，利用转化思想，通过连接CO并延长交⊙O于P，把图形分解为两个基本题型(图3)进行解决.

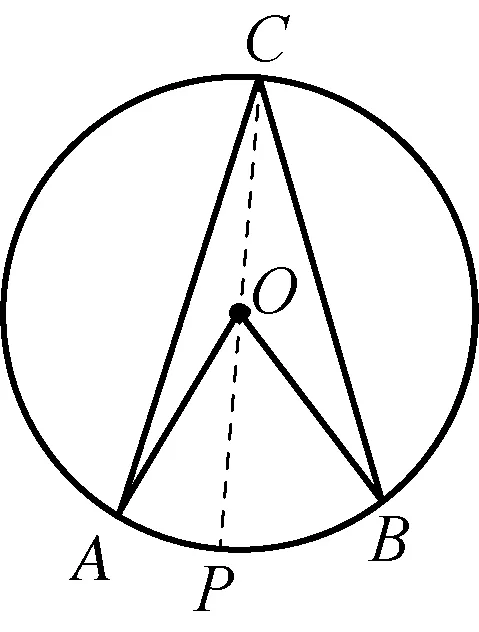
图2

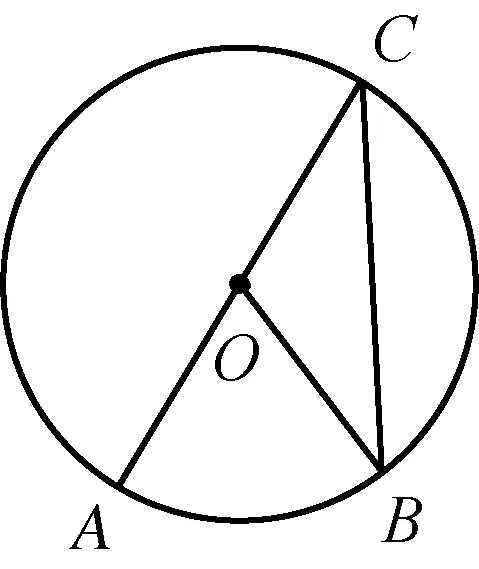
图3

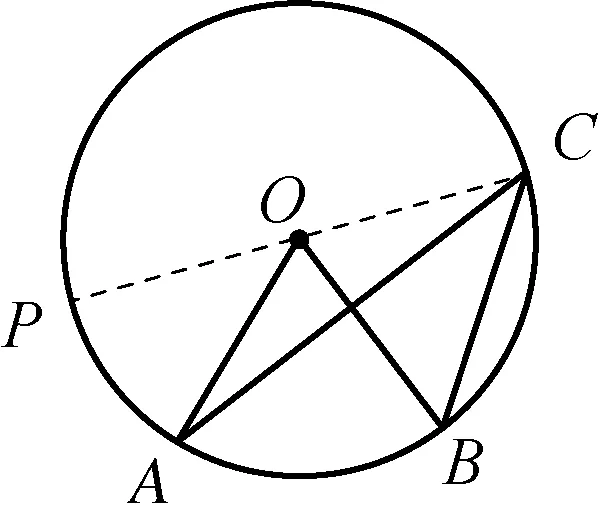
图4

部分学生通过数学实验，又发现：当点C在圆上运动时候，∠AOB=2∠ACB；当点C在圆外，∠AOB>2∠ACB；当点C在圆内，∠AOB<2∠ACB.实验的结果已经超出了文本提供的圆周角定理.技术的引入，使得数学问题直观化，便于学生发现问题和提出问题，激发数学探究热情.

教师要树立正确的作业观.站在理解数学、理解学生、理解教学、理解技术的视角下提高作业设计的质量，减轻学生课业负担，充分激发数学学习的主动性与积极性，帮助学生学会学习，发展学生的核心素养、促进学生全面发展.