从2022年高考试题再看函数图像的双对称问题

孙丕训(特级教师) 王丽君

(北京陈经纶中学)

函数的性质是高中数学重要的学习内容,也是高考的必考内容.函数的对称性是函数的重要性质,也是高考的考查热点.从历年高考试题来看,对函数对称性的考查,题目越来越新颖,对思维能力的要求也越来越高.在2022年新高考Ⅰ卷和全国乙卷中,选择题的最后一题都是函数对称性问题,而这两道题都可以转化成函数图像的双对称问题(即函数图像关于两条直线对称,或关于两个点对称,或关于一条直线及一个点对称).

首先,关于函数图像的对称性,有性质1、性质2.

性质1如果对于函数f(x)在定义域R 内的任意一个x,都有f(a＋x)＝f(a－x),则函数f(x)的图像关于直线x＝a对称;反之,若函数f(x)的图像关于直线x＝a对称,则有f(a＋x)＝f(a－x)(如图1).

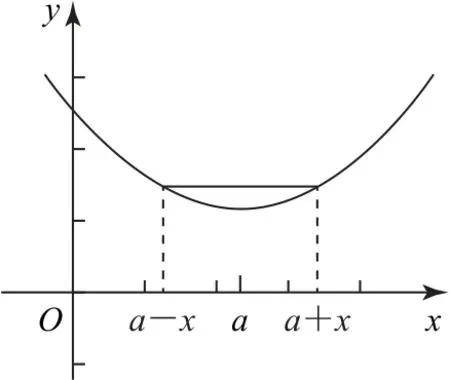
图1

特别地,当a＝0时,函数f(x)为偶函数.

性质2如果对于函数f(x)在定义域R内的任意一个x,都有f(a＋x)＋f(a－x)＝2b,则函数f(x)的图像关于点(a,b)对称;反之,若函数f(x)的图像关于点(a,b)对称,则有f(a＋x)＋f(a－x)＝2b(如图2).

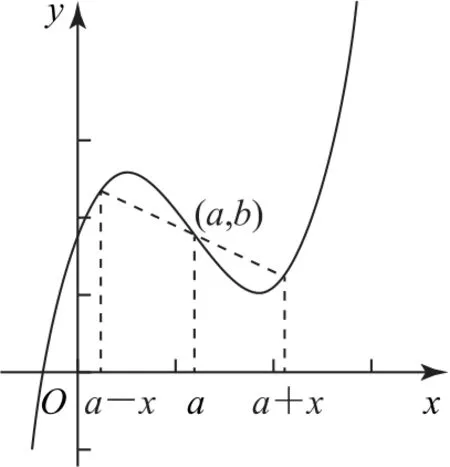
图2

特别地,当a＝0,b＝0时,函数f(x)为奇函数.

函数图像的双对称问题,往往隐含着周期性,如性质3、性质4、性质5.

性质3如果函数f(x)的定义域为R,且函数f(x)的图像既关于直线x＝a对称,又关于直线x＝b对称(a≠b),那么函数f(x)必为周期函数,其中一个周期为

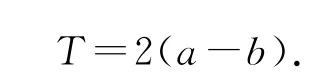
证明因为函数f(x)的图像关于直线x＝a对称,所以f(a＋x)＝f(a－x),即

又因为f(x)的图像关于直线x＝b对称,所以f(b＋x)＝f(b－x),即

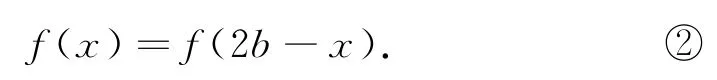
由①和②得f(2a－x)＝f(2b－x),将x换为2bx,则f(x＋2a－2b)＝f(x),所以f(x)为周期函数,其中一个周期为T＝2(a－b).

性质4如果函数f(x)的定义域为R,且函数f(x)的图像既关于点(a,t)对称,又关于点(b,t)对称(a≠b),那么函数f(x)必为周期函数,其中一个周期为T＝2(a－b).

证明过程与性质3类似,在此不再赘述.

性质5如果函数f(x)的定义域为R,且函数f(x)的图像既关于直线x＝a对称,又关于点(b,t)(a≠b)对称,那么函数f(x)必为周期函数,其中一个周期为T＝4(a－b).

证明因为函数f(x)的图像关于直线x＝a对称,所以f(a＋x)＝f(a－x),即

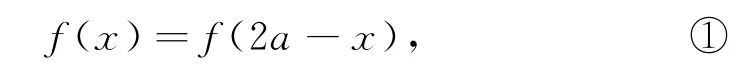
又因为函数f(x)的图像关于点(b,t)(a≠b)对称,所以f(b＋x)＋f(b－x)＝2t,即

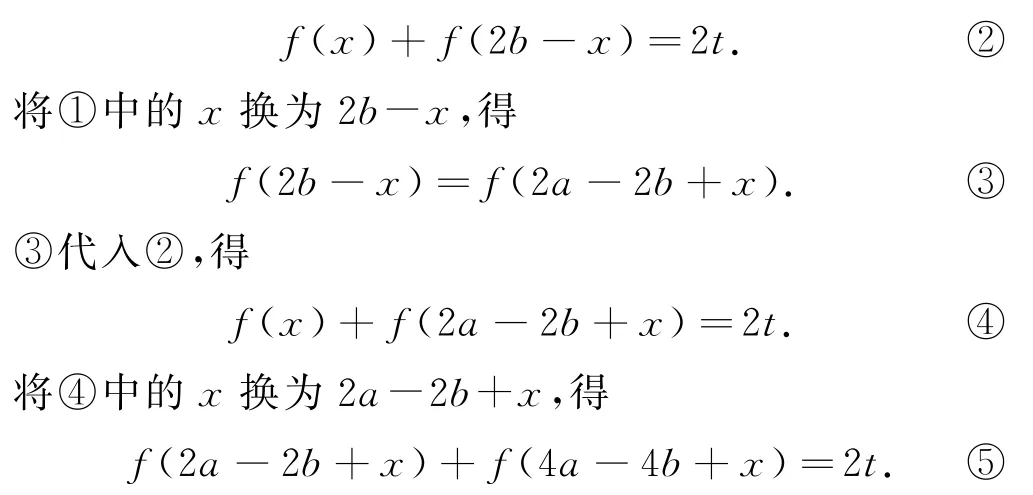
由④和⑤得f(x)＝f(4a－4b＋x),所以函数f(x)为周期函数,其中一个周期为T＝4(a－b).

下面我们应用以上性质解决2022年高考中选择题的压轴题.

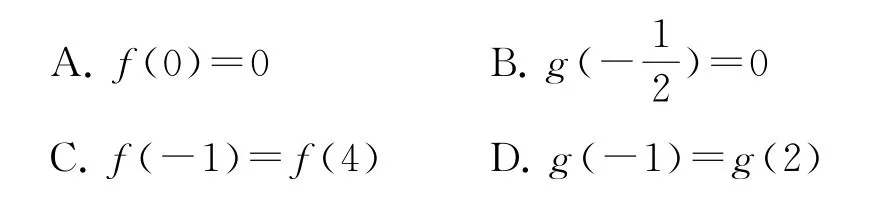
例1(2022年新高考Ⅰ卷12,多选题)已知函数f(x)及其导函数f′(x)的定义域为R,记g(x)＝f′(x).若,g(2＋x)均为偶函数,则( ).

由g(2＋x)为偶函数得g(2＋x)＝g(2－x),所以g(x)关于直线x＝2对称.

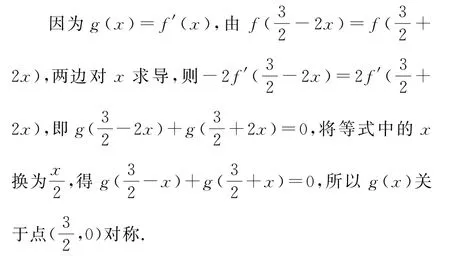
由性质5,可知函数g(x)的一个周期为

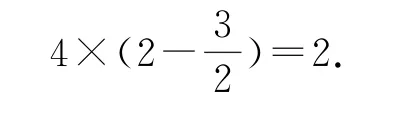
由g(2＋x)为偶函数,则g(2＋x)＝g(2－x),所以f′(2＋x)＝f′(2－x),即(f(2＋x)＋f(2－x))′＝0,所以f(2＋x)＋f(2－x)＝t(t为常数),所以f(x)关于点对称.同理可得,函数f(x)的一个周期为

综上,函数f(x)与g(x)均是周期为2的周期函数,所以,常数t可取任意实数,A不正确.另外,对于选项A 的排除,也可根据已知条件知:若函数f(x)满足已知条件,则函数f(x)＋C(C为常数)也满足条件,所以无法确定f(0),故A 不正确.

综上,故选BC.

不可否认，传统报纸在读者的心中权威性很高，得到大家的一致认可，现在虽然我们利用网络能够获得各种各样的新闻，但是网上新闻的质量参差不齐，有好有坏，碎片化的现象非常明显。而且，有时候为了博得人们眼球，会散布虚假信息。报纸可以和互联网结合起来，找到切入点，寻找适合报纸刊登的新闻选题，不断挖掘新闻的价值，利用报纸媒体优势围绕选题进行全方位的报道，利用报纸媒体的影响力优化网络上的热门话题，不断扩展报纸媒体的空间，让报纸媒体和互联网共赢。

点评求解本题的关键是通过g(x)＝f′(x)的关系,对关于f(x)的等式两边求导、对g(x)的等式积分(导数的逆运算),得到f(x)与g(x)的另一组体现对称性的关系式,进而得出函数的周期性,从而解决问题.

本题为多选题,正确的选项需推理得到,错误的选项可用排除法.在得到g(－1)＋g(2)＝0时,并不能排除选项D,这是因为当g(－1)＝g(2)＝0时,D仍可能正确,要排除D,需说明g(－1)不一定为0,根据函数f(x)的对称性,不难举出满足条件的一个函数f(x)＝sinπx,此时,g(－1)≠g(2),故排除选项D.另外,f(x)＝sinπx＋C(C为常数)均符合条件,可迅速排除A 和D.

例2(2022年全国乙卷理12)已知函数f(x),g(x)的定义域均为R,且f(x)＋g(2－x)＝5,g(x)－f(x－4)＝7,若y＝g(x)的图像关于直线x＝2对称,g(2)＝4,则

解析因为g(x)关于直线x＝2对称,所以g(2＋x)＝g(2－x).因为

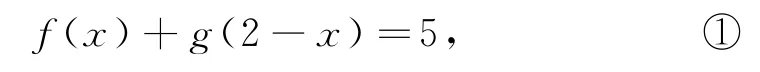
将①中的x换成－x,得

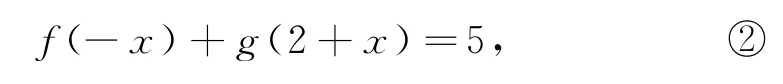
①－②,得f(x)＝f(－x),即f(x)为偶函数,f(x)关于直线x＝0对称;在g(x)－f(x－4)＝7中,将x换成x＋2,得

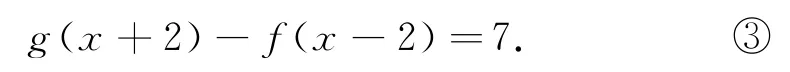
②－③,得f(－x)＋f(x－2)＝－2,即f(x)关于点(－1,－1)对称,应用性质5,f(x)的一个周期为4.

在式①中,令x＝0,得f(0)＋g(2)＝5,又因为g(2)＝4,所以f(0)＝1,在f(－x)＋f(x－2)＝－2中,令x＝1,则f(－1)＝－1,再由f(x)＝f(－x),可得f(1)＝f(－1)＝－1,因为f(x)的周期为4,所以f(2)＝f(－2)＝－2－f(0)＝－3,f(3)＝f(－1)＝－1,f(4)＝f(0)＝1,所以

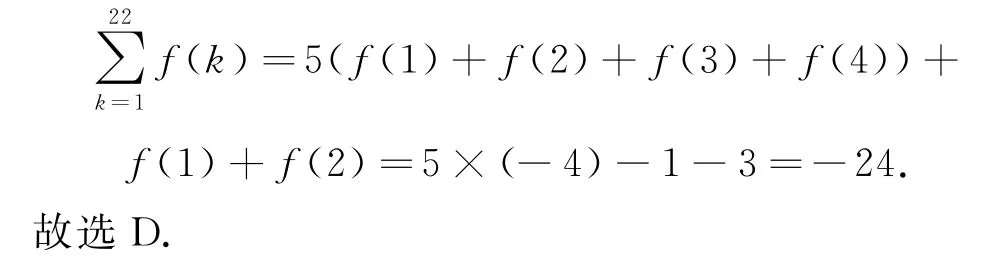
点评求解本题的关键是利用方程的思想,由g(2＋x)＝g(2－x)这个关系式,结合已知条件中的两个等式,运用消元法得到f(x)的对称轴和对称中心,进而得出函数的周期,问题得以解决.

函数图像的双对称性质能得出函数的周期性,把握这个本质在解决问题过程中能起到事半功倍的作用.最后,给出4个练习,均选自近几年高考真题,都是抽象函数的双对称问题,题干简洁,内容丰富,读者可以利用以上性质试一试.

链接练习

1.(2021年新高考Ⅱ卷8)已知函数f(x)的定义域为R,f(x＋2)为偶函数,f(2x＋1)为奇函数,则( ).

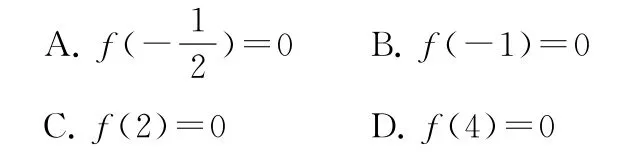
2.(2021 年全国甲卷理12)设函数f(x)的定义域为R,f(x＋1)为奇函数,f(x＋2)为偶函数,当x∈[1,2]时,f(x)＝ax2＋b,若f(0)＋f(3)＝6,则

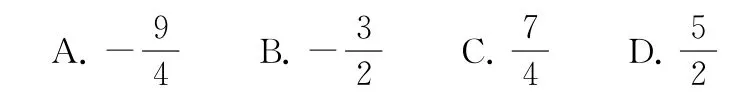
3.(2021年全国甲卷文12)设f(x)是定义域为R 的奇函数,且f(1＋x)＝f(－x).若

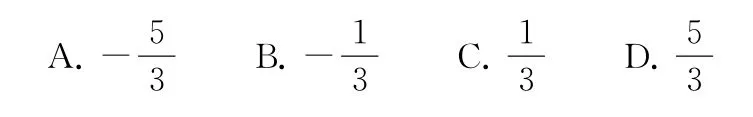
4.(2018年全国Ⅱ卷理11)已知f(x)是定义域为(－∞,＋∞)的奇函数,满足f(1－x)＝f(1＋x).若f(1)＝2,则f(1)＋f(2)＋f(3)＋…＋f(50)＝( ).

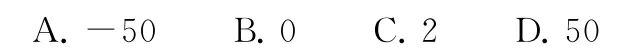
链接练习参考答案

1.B. 2.D. 3.C. 4.C.

(完)