从一道强基计划“关联”函数图像试题谈起
刘文明
(山东省德州市临邑第一中学)
“关联”函数的图像识别问题重点考查的是函数图像,在2020年复旦大学强基计划试题中就涉及了此类问题.
母题已知f(x)的图像如图1所示,则f(f(x))的大致图像为( ).

图1

解析注意到f(1)=f(-1)=0,f(0)=-1,f(x)为偶函数,所以f(f(x))为偶函数,故A,D 错误.当x0∈(0,1)时,f(x0)∈(-1,0),此时f(f(x0))<0,所以C错误,故选B.
设函数y=f(u)的定义域为Df,函数u=g(x)的定义域为Dg,且g(x)的值域Rg⊂Df,则y=f(g(x))(x∈Dg)称为由函数u=g(x)与函数y=f(u)构成的复合函数,它的定义域为Dg.
从母题中可以看出,这类试题命制的模式是根据所给函数的图像,判断复合后函数的图像.这类题目的特点是给出一个函数的图像,然后判断与其相关的新函数图像.
这道试题的命题思路,引发了笔者的思考,这类“关联”式函数图像试题还存在哪些其他的命题模式,下面笔者沿着这一思路进行探究.
例1函数y=f(x)的图像如图2所示,则函数的图像大致是( ).
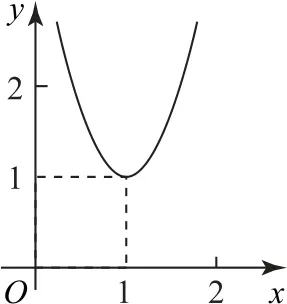
图2

解析由函数y=f(x)的图像知,当x∈(0,2)时,f(x)≥1,所以.又因为函数f(x)在(0,1)上单调递减,在(1,2)上单调递增,所以)在(0,1)上单调递增,在(1,2)上单调递减.结合各选项知C正确.
点评本题通过所给函数的图像,让学生识别底数为的对数函数图像,较好地考查了学生的推理论证能力.
例2已知函数y=f(x)的图像如图3所示,则其导函数y=f′(x)的图像可能是( ).
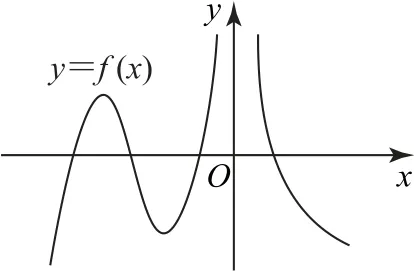
图3

解析由题意知函数y=f(x)在(0,+∞)上单调递减,则其导函数在(0,+∞)上恒小于0,排除B和D.又因为函数y=f(x)在(-∞,0)上先单调递增,后单调递减,再单调递增,则其导函数在(-∞,0)上先大于0,后小于0,再大于0,排除C,故选A.
点评虽然本题也是一道“关联”函数图像问题,但与例1有本质上的区别,这道题将函数图像与导函数的图像进行了有机结合,需要学生熟练掌握函数的单调性与导数的关系.
例3设函数f(x)的导函数f′(x)图像如图4所示,则函数y=f(x)的图像可能为( ).

图4
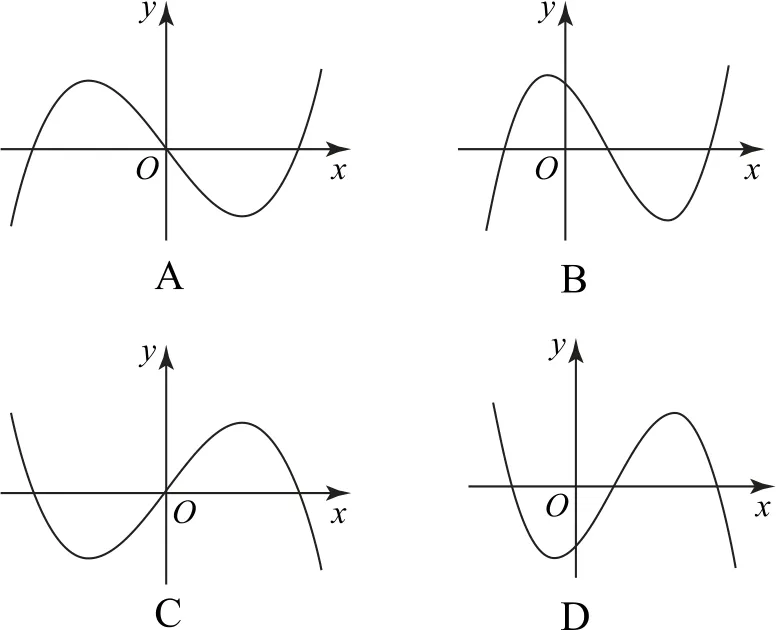
解析由导函数的图像可知,函数y=f′(x)的符号从左至右依次为负、正、负,则函数y=f(x)的单调性从左至右依次为单调递减、单调递增、单调递减,排除A,B.
由导函数的图像可知,函数y=f′(x)为偶函数,即f′(-x)=f′(x),构造函数g(x)=f(x)+f(-x),则g′(x)=f′(x)-f′(-x)=0,所 以f(x)+f(-x)=a(a为常数),则函数y=f(x)的图像关于点对称,排除D.
综上,故选C.
点评根据导函数y=f′(x)的符号与原函数y=f(x)单调性之间的关系,结合导函数为偶函数这个隐含条件即可得出正确的答案.
例4在同一平面直角坐标系中,函数(a>0 且a≠1)的图像可能是( ).

解析当0<a<1时,函数y=ax过定点(0,1)且单调递减,则函数过定点(0,1)且单调递增,函数过定点且单调递减,D 选项符合.当a>1时,函数y=ax过定点(0,1)且单调递增,则函数过定点(0,1)且单调递减,函数且单调递增,各选项均不符合.故选D.
点评本题是两个函数的图像识别问题,它们之间的关联性在于通过变量a构建了桥梁.在讨论a的不同取值情况时,需要分别讨论指数函数、对数函数图像的单调性和变量a的联系,再结合选项得出正确结论.对函数的图像和性质掌握不扎实,容易导致判断失误.
(完)

