近年来活跃在强基、竞赛中的递推数列
李锦旭(特级教师)
(北京市育英学校)
本文针对近些年来在自主招生、强基计划、竞赛试题中出现的以递推数列为背景的试题,择要分类予以解析,并以点评的形式对其中典型试题的命制背景、引申推广等基本命题特点和试题蕴含的规律进行初步探讨.
1 通过简单变形转化为等差或等比数列型
例1(2019 年北京大学自主招生)已知数列ak+ak+1=4k+3(k=1,2,…),则a2+a2020=( ).

解析由ak+ak+1=4k+3,可得
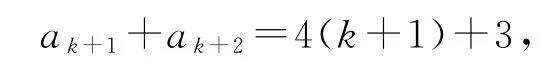
两式相减可得ak+2-ak=4,所以

即a2020=a2+4036.因此

由于a2无法确定,所以a2+a2020也无法确定,故选D.

显然,当n=4时,xn=3∈Z,故n的最小值为4.
2 线性分式型
例3(2019年中国科学技术大学自主招生)数列{xn}满 足:,则

点评对于线性分式型,若分子不含常数项,则可直接取倒数转化为an+1=pan+q型.若分子含常数项,则需适当换元再取倒数转化.
例4(2019年福建省预赛)已知数列{an}满足,2an+1an-7an+1-3an+12=0(n∈N*).
(1)记cn=an-2,求数列{cn}的通项公式;
解析(1)将an=cn+2代入

化简可得


又因为当n=1 时,,所以[b1]=1;当n≥2时,[bn]=2(n-1).于是,当n≥2时,有

由n2-n+1≤2019以及n∈N*,得n≤45,所以使[b1]+[b2]+[b3]+…+[bn]≤2019成立的最大正整数n的值为45.
3 线性交叉互动型递推数列
例5(2017年清华大学自主招生与领军试题)已知数列{xn},{yn},{zn}满足

解析根据对称特点,将①②③相加得
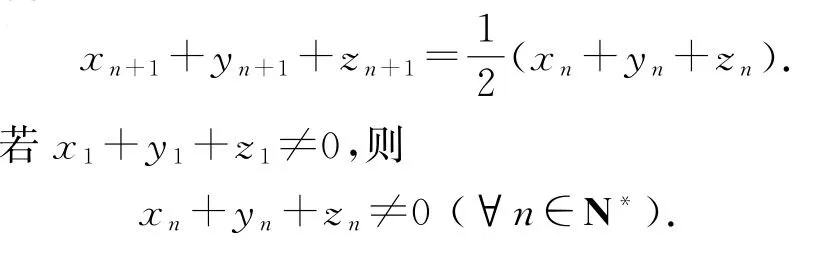
可得{xn+yn+zn}是以x1+y1+z1为首项,以为公比的等比数列.
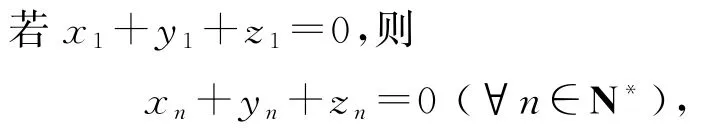
即数列{xn+yn+zn}的各项均为0,不是等比数列,故A 错误.

对于D,若存在正整数m使得xm=ym=zm=a,代入式①②③可得
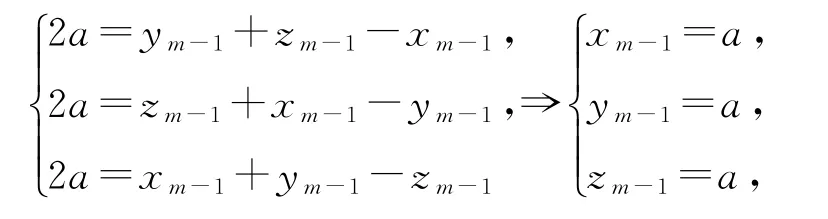
一直递推下去可得x1=y1=z1=a,故D 正确.
综上,故选BD.
点评本题改编于如下竞赛原题,有兴趣的读者可尝试证明:
设a,b,c>0,数列{xn},{yn},{zn}中,x1=a,y1=b,z1=c,且,yn+1=.试求证:若xn>0,yn>0,zn>0,则a=b=c.
4 连续三项型递推数列
例6(2019年浙江省预赛)设0≤x1≤x2,数列{xn}满足xn+2=xn+1+xn,n≥1.若1≤x7≤2,则x8的取值范围是________.
解析将后面的各项用前两项表示,可得
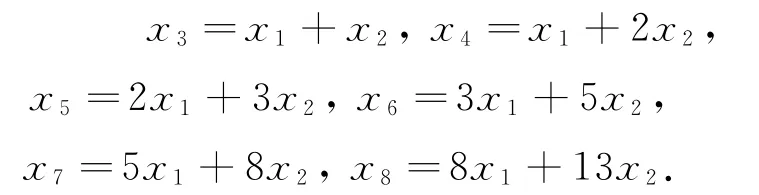
因为1≤x7≤2,所以1≤5x1+8x2≤2.结合0≤x1≤x2考虑线性规划,在x1Ox2坐标系中所围成的图形为四边形,其顶点坐标为,所以
例7(2011年清华大学等七校联考自主招生)将一枚质量均匀的硬币连续抛掷n次,以pn表示未出现连续3次正面的概率.
(1)求p1,p2,p3,p4;
(2)探究数列{pn}的递推公式;
(3)讨论数列{pn}的单调性及其极限,并阐述该极限的概率意义.
解析(1)显然p1=p2=1,,下面求p4.投掷4 次连续出现3 次正面向上的情况只有“正正正正”“正正正反”“反正正正”,共3种.而投掷4次的所有可能的情况有16种,故
(2)分三种情况(第n次、第n-1次、第n-2次都出现正面的情况不包含在pn内).
如果第n次出现反面,那么前n次不出现连续3次正面与前n-1次不出现连续3次正面是相同的,此时不出现连续3次正面的概率为--
如果第n次出现正面,第n-1次出现反面,那么前n次不出现连续3次正面与前n-2次不出现连续3次正面是相同的,此时不出现连续3次正面的概率为
如果第n次出现正面,第n-1 次出现正面,第n-2次出现反面,那么前n次不出现连续3次正面与前n-3次不出现连续3次正面是相同的,此时不出现连续3次正面的概率为
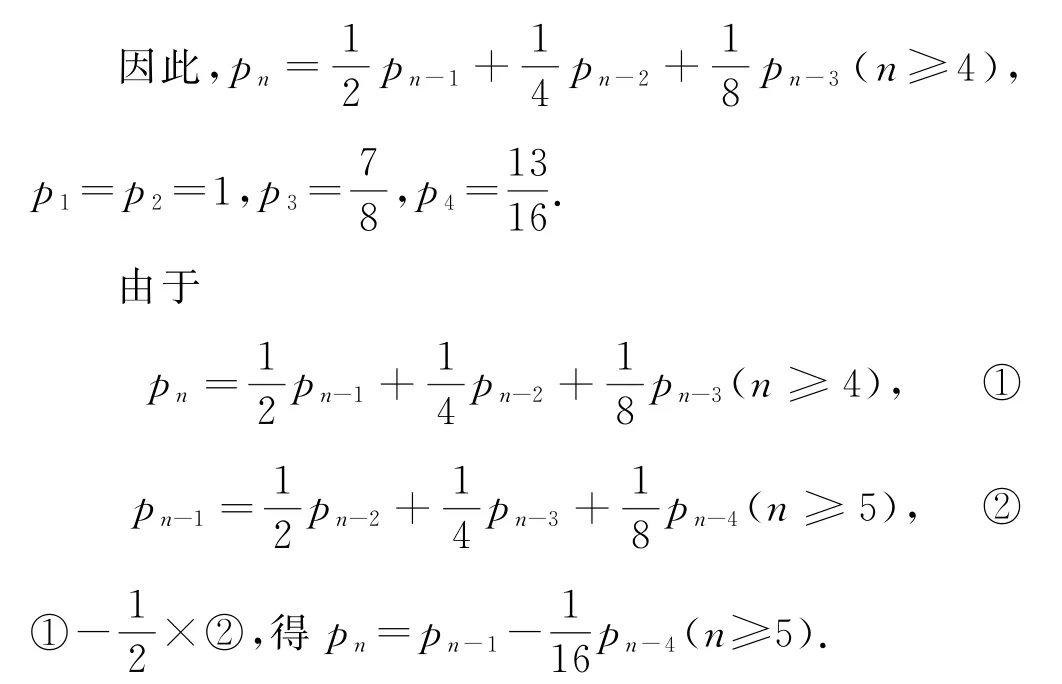
(3)所以当n≥5时,数列{pn}单调递减且p5=,又易得p1=p2>p3>p4,故当n≥2时,数列{pn}单调递减.
当n≥2时,数列{pn}单调递减且有下界,所以数列{pn}的极限存在,设为p.对两边取极限,得,解得p=0.
其统计意义是:当投掷的次数足够多时,未出现连续3次正面的概率非常小,趋近于零.
5 递推数列与其他知识的交会融合
例8(2019年重庆市预赛)数列{an}满足a1=3,a2=6,
(1)求证:数列{an}是正整数数列;
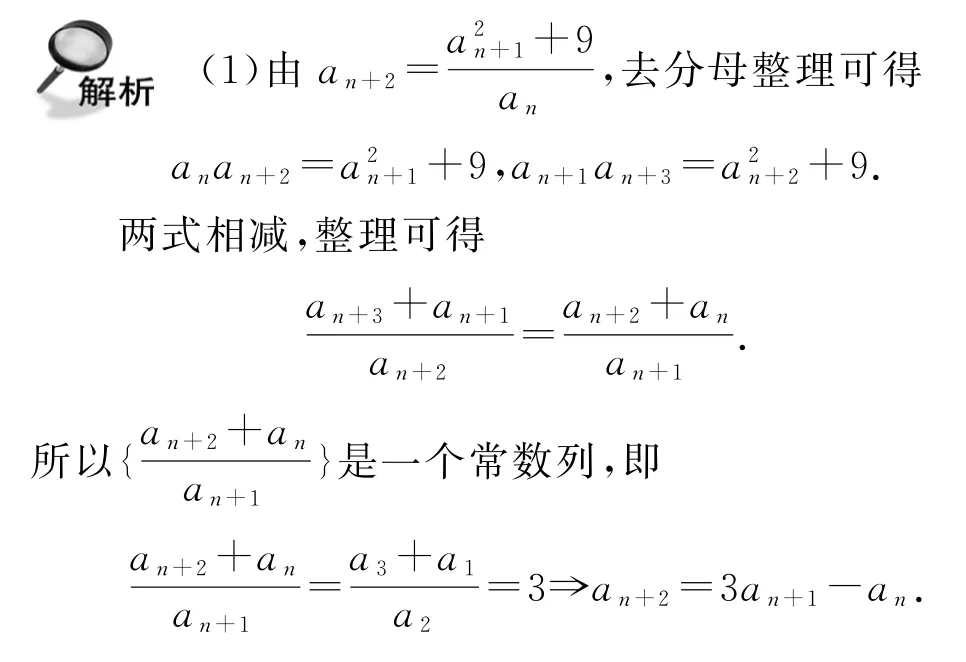
(2)是否存在m∈N*,使得2019|am? 并说明理由.又a1=3,a2=6,,所以an>0,从而{an}是正整数数列.
(2)由于2019=3×19×37,假设2019|am,则19|am;由a1=3,a2=6及an+2=3an+1-an可得
an≡3,6,15,1,7,1,15,6,3,3,6,…(mod19).
即19不能整除an,当然2019|am也不成立.
例9(2016年清华大学自主招生与领军)数列{an}满足a1=5,a2=13,则( ).
A.an+2=5an+1-6an
B.an都是整数
C.an>4n
D.an与2015最接近的项是a7
解析因为难以由所给递推公式直接求通项公式,故采用结合选项验算(或验证)的方法求解.对于选项A,根据特征根法可知an=2n+3n,代入,发现是成立的,而这个递推数列确定的数列是唯一的,因此可以确定选项A 正确,显然选项B正确.
对于选项C,显然错误,因为a3=35<43.
对于选项D,an是单调递增的,a7=2315>2015(相差200),a6=793<2015(相差1222),所以易知a7与2015最接近,故选项D 正确.
综上,故选ABD.
例10(2021年中国科学技术大学创新班)已知g0(x)=1,g1(x)=x,证明:gn(x)为n次整系数多项式,并求gn(x)=0的所有根.
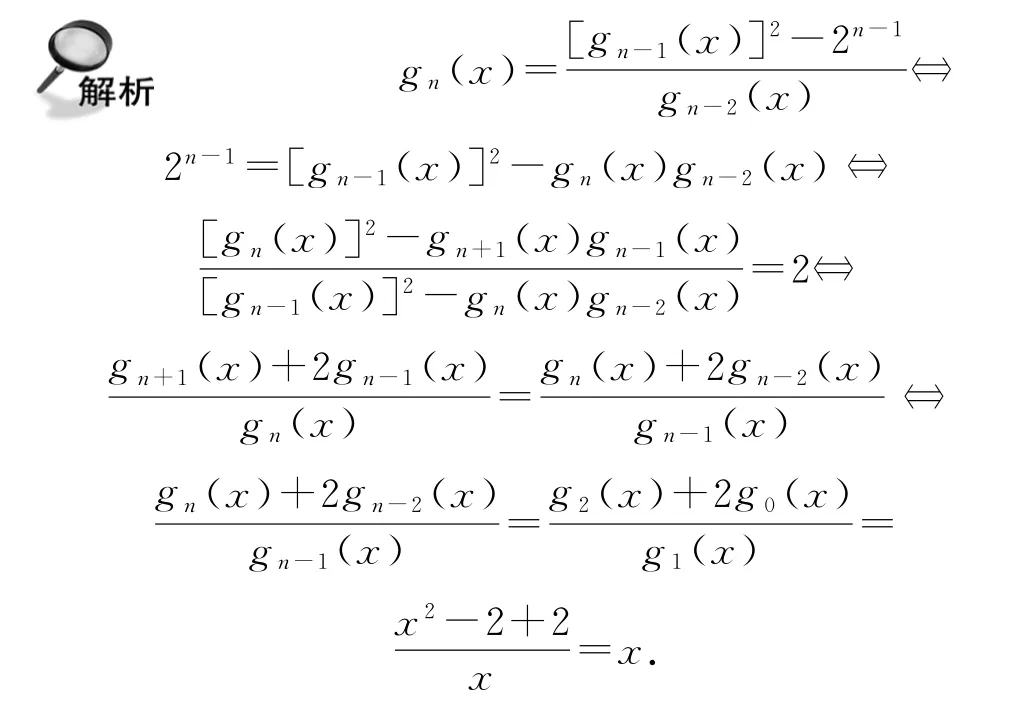
所以gn(x)=xgn-1(x)-2gn-2(x).又g0(x)=1,g1(x)=x为整系数多项式,所以则由数学归纳法可知,gn(x)为n次整系数多项式.

6 真题练习
1.(2021年北京大学强基计划)已知实数x0∈[0,1),数列{xn}满足:若,则xn=2xn-1;若,则xn=2xn-1-1(n=1,2,3,…).现知x0=x2021,则可能的x0的个数为_________.
2.(2021年北京大学强基计划)已知数列{an}满足a1=2,an+1=2an;数列{bn}满足b1=2,bn+1=5bn.若正整数m满足bm>a25,则m的最小值为______.
3.(2019年清华大学领军)对正整数n,设整数xn,yn满足,则( ).
A.对每个正整数n,有xn+1=2xn+3yn
B.对每个正整数n,有yn+1=xn+2yn
C.存在正整数n,使得xn=2019
(完)

