基于深度学习的微专题复习教学探析
——以“解析几何中探究型存在性问题微专题”为例
广东 潘敬贞 陈焕涛
学业质量水平标准和高中数学核心素养是《普通高中数学课程标准(2017年版2020年修订)》的两大亮点,贯穿高中数学教学的始终.随着“三新”(新课标、新教材、新高考)的全面实施,高三数学复习教学也面临新的挑战,如何在高三阶段以知识为载体,培育学生的数学“四基”与“四能”,发展学生的数学核心素养,最终让学生在高中数学终极评价(高考)中获得理想的成绩,是每一位高三数学一线教师面临的实际问题.
高一、高二新授课的教学通常是在学生不知晓学习内容的情况下进行的,而高三数学复习则是在学生已经学习过相关内容,但相隔时间较长,遗忘较多的状态下进行的,而且其教学目标更是直接指向高中阶段的终极评价即高考.高三数学复习分为三个轮次,一轮复习重基础、讲知识、建体系,二轮复习的关键在于知识点的深入、重难点的突破、思想方法的交融升华,三轮复习则侧重查漏补缺,重难点强化.微专题因微而“专”,因微而“精”,因微而“深”,因此微专题具有实效性、针对性、灵活性、细致性、深刻性等特点,在三个轮次的复习中起到重要作用.在学生学习困难处设置微专题、在思维痛点处设置微专题、在核心内容与高频考点处设置微专题能有效引领学生进行深度学习.
解析几何是高中数学的核心内容,是高中数学教学的重点与难点,也是考查推理论证能力和运算求解能力的绝佳素材,同时也是培育数学运算核心素养的沃土.解析几何中探究型存在性问题具有较强的开放性、探索性和综合性,解析几何中探究型存在性问题对培育学生的创新意识、应用意识,培育学生的理性精神,发展核心素养具有重要意义.该类问题的求解重点考查运用代数方法研究几何问题,主要涉及平面几何的性质、直线方程、韦达定理、点到直线的距离公式、分类讨论等解析几何的核心内容,在此过程中推理论证能力尤为关键.近年来,解析几何中有关面积问题(三角形和四边形的面积)一直是高考命题的热点,常以压轴题的形式出现.
本文首先以学生熟悉的三角形面积问题和两条直线垂直问题为素材,考虑运算量不要太大,因此以一条直线与抛物线相交问题为背景,编制一个基本问题的问题(问题1),目的是调动全体学生积极动手求解并参与课堂,同时使学生初步认识探究型存在性问题及其一般求解思路.在问题1的基础上,以直线与椭圆相交为背景,结合平面解析几何常见的直线斜率问题、角的问题、平面向量数量积问题、距离问题、弦长问题等设置变式(变式1-5),目的是让学生在不同的几何元素下,合理地转化以及将其代数化,最后解决问题,从而进一步提升学生的数学“四基”与“四能”,发展学生的数学核心素养.为了进一步扩大问题的开放性与综合性,全面提升学生的数学能力,因此引入参数,设置“是否存在这样的常数”(问题2),探究曲线的存在性,设置“是否存在这样的曲线”(问题3及变式6、7),这两类问题都具有较高的开放性和较强的综合性,对培育学生的理性思维和发展数学核心素养具有重要意义.
1.是否存在这样的点
点是构成几何图形的重要元素,因此以“点”为切入点,以存在性探究型设问,受到众多命题专家的青睐,主要考查用代数方法解决解析几何中的直线斜率、两条直线所成角、距离、平面向量的数量积等问题,问题1及变式1-5主要围绕“是否存在这样的点”进行分析求解.
问题1.已知直线l:2x-3y+4=0与抛物线C:y2=4x交于A,B两点.
(1)能否在x轴上找到点P,使得△PAB的面积为4?若存在,求出点P的坐标,若不存在,请说明理由.
(2)能否在x轴上找到点P,使得∠APB=90°?若存在,求出点P的坐标,若不存在,请说明理由.
设计意图:首先选一个难度较低、计算量不大,但又要涵盖解析几何的基本知识、基本方法,能够起到承上启下作用的问题作为本文的切入点.众所周知,直线与抛物线的位置关系问题,相对于直线与椭圆、直线与双曲线的位置关系问题计算量要少很多,因此问题1以一条直线与抛物线相交问题为背景,围绕本节课的主题(探究型存在性问题)设置问题.第(1)问结合大家熟悉的三角形问题设问;第(2)问以90°为背景元素设置问题,学生可以从直线斜率角度思考,也可以借助平面向量工具进行解题,为解决问题提供多种思路.第(1)问的结论存在,而第(2)问的结论不存在,让学生从正反两方面认识探究型存在性问题的“探索性”与“开放性”,初步体会该类问题的求解思路,厘清解答步骤.
【解析】(1)假设存在.
把直线2x-3y+4=0代入抛物线y2=4x消x并整理得y2-6y+8=0,
设A(x1,y1),B(x2,y2),P(a,0),
则y1+y2=6,y1y2=8,
点P(a,0)到直线l的距离
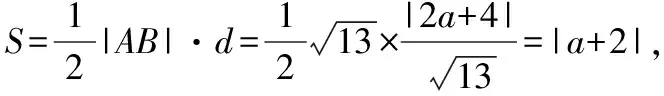
所以|a+2|=4,解得a=2或a=-6,
因此,所有满足条件的P的坐标为(-6,0)和(2,0).
评注:第(1)问的求解,首先假设存在,进而设点P的坐标,再利用点到直线的距离公式求三角形的高,利用弦长公式求三角形的底,然后根据三角形面积公式列方程,若方程有解,则将方程的根解出来即可.问题较为基础,难度较低,大多数学生都能快速完成求解.
(2)思路一(向量法):假设存在.
设A(x1,y1),B(x2,y2),P(a,0),

若存在点P,使得∠APB=90°,
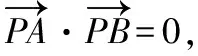
所以(x1-a)·(x2-a)+y1y2=0,
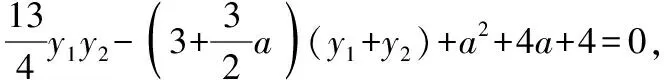
又由(1)得y1+y2=6,y1y2=8,
所以得a2-5a+12=0,此方程无解,故不存在这样的点P.
思路二(直线斜率法):
假设存在点P(a,0),使得∠APB=90°,
则直线PA⊥PB.
若直线PA,PB的斜率存在,设A(x1,y1),B(x2,y2),

所以(x1-a)·(x2-a)+y1y2=0,
下同思路一,直线PA或PB的斜率不存在,显然不成立,故不存在这样的点.
评注:在第(1)问的基础上,以“90°”为元素设置问题,该题的求解,首先要合理将角代数化,可采用平面向量工具,也可以用直线斜率进行转化,最后根据题意所列的方程无解,因而得出假设不成立的结论.
1.1 直线的斜率问题
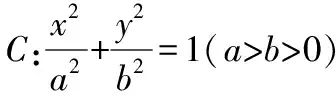
(1)求椭圆C的方程;
(2)在x轴上是否存在一点T,使得直线TM与TN的斜率之积为定值?若存在,请求出所有满足条件的点T的坐标;若不存在,请说明理由.
设计意图:有了问题1的求解经验,问题1的第(2)题的思路二也用到了直线斜率法.同时为了进一步深入研究“探究型存在性问题”,提升学生的运算求解能力,因此变式1以直线与椭圆相交为背景,结合直线斜率法,设置探究型存在性问题.变式1的求解思路与问题1基本一致,但运算量增加了不少,笔者认为此处增加运算量是有必要的,为后续的深度学习奠定了基础,同时引导学生反设直线方程可以有效减少运算量,优化解题过程,提高解题效率,积累解题经验.
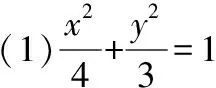
(2)因为直线l过点F2(1,0)且不与x轴重合,
所以设l的方程为x=my+1,
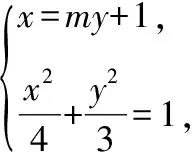
消去x并整理得(3m2+4)y2+6my-9=0,
Δ=36m2+36(3m2+4)>0,
设M(x1,y1),N(x2,y2),
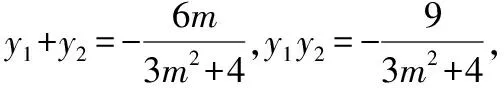


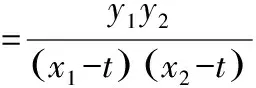

因此,所有满足条件的T的坐标为(-2,0)和(2,0).
评注:本题以直线与椭圆为背景,相对问题1,运算量大大增加,反设直线方程可以有效减少运算量.该题求解的关键是用坐标表示直线斜率并化简求值,本题的求解对培育学生的运算求解能力,提升推理论证能力有着重要意义.
1.2 角的问题
“角”是平面几何的基本元素,用代数方法解决几何问题是解析几何的核心,用坐标表示“角”的问题是将“角”的问题代数化的有效途径,因此保留直线与椭圆相交的背景,将“角”相等问题转化为直线斜率和为零得到变式2,变式将平面解析几何的基本概念和基本性质转化为直线的斜率问题,从而顺利将问题代数化.让学生进一步体验用代数方法解决几何问题(解析几何的本质),同时进一步提升学生分析与解决问题的能力、化归与转化思想和运算求解能力等.

(1)求椭圆G的方程;
(2)过点M(0,1)斜率为k(k≠0)的直线l交椭圆G于A,B两点,在y轴上是否存在点N使得∠ANM=∠BNM(点N与点M不重合),若存在,求出点N的坐标;若不存在,请说明理由.
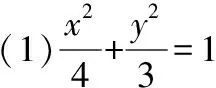
(2)设直线l:y=kx+1(k≠0),A(x1,y1),B(x2,y2),N(0,y0),
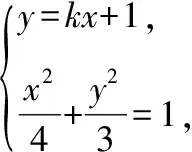
消去y并整理得(4k2+3)x2+8kx-8=0,
Δ=64k2+32(4k2+3)>0,
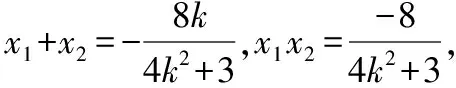
因为∠ANM=∠BNM,所以kAN+kBN=0,
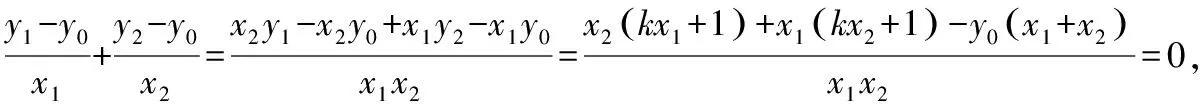
即2kx1x2+(1-y0)(x1+x2)=0,
得y0=3,即存在定点N(0,3).
评注:变式2以“角”为元素,问题求解的关键也是将“角”的问题代数化,进而联立直线与曲线方程,通过一系列的运算推理,最终将问题解决.
1.3 向量的数量积问题
平面向量是处理平面解析几何问题的有利工具,也是沟通几何与代数的重要桥梁,以平面向量的数量积设问是解析几何中常见的问题.因此保留直线与椭圆相交的背景,结合平面向量的数量积设置探究型存在性问题得到变式3.

(1)求椭圆C的方程;


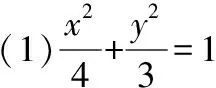

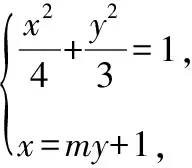
消去x得(3m2+4)y2+6my-9=0,





1.4 距离问题
学生经历了问题1与变式1-3的分析与求解,积累了处理解析几何的一般方法,掌握了解析几何中“探究型存在性问题”的一般策略,此时给出一道高考真题(2020年新高考山东卷),让学生感受高考真题,确定努力方向.

(1)求椭圆C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

评注:第(2)问透过条件AM⊥AN可知△MAN为椭圆的内接直角三角形,也可以理解为点A(2,1)在以MN为直径的圆上,试题中的基本元素动中有静,要求证|DQ|为定值,则必须化动为静,可见试题的难度较大.但是如果在平时的学习过程中善于观察,敢于探究,积累学习活动经验,对该题的解答是不存在问题的.该题的解答可以设动直线MN的方程为x=my+n,也可以设动直线MN的方程为y=kx+m,但是后者需要对斜率是否存在分类讨论.解决该题的关键是要能够找出动直线MN所过的定点坐标,然后再根据直角三角形的基本性质得出答案.
1.5 弦长问题
变式5.已知圆O:x2+y2=64,圆C与圆O相交,圆心为C(9,0),且圆C上的点与圆O上的点之间的最大距离为21.
(1) 求圆C的标准方程;
(2) 在x轴上是否存在定点P,使得过点P的动直线l被圆O与圆C截得的弦长d1,d2的比值总等于同一常数λ?若存在,求点P的坐标及λ的值,若不存在,说明理由.
【解析】(1) (x-9)2+y2=16(过程略).
(2) 假设存在符合题意的定点P(x0,0),
当直线l的斜率存在时,
设直线l的方程为y=k(x-x0),即kx-y-kx0=0,
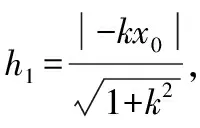




两边平方得,
整理得,

由于对任意实数k,上式均成立,故有

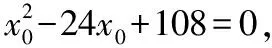

故存在定点P(6,0)或P(18,0),使得d1,d2的比值总等于同一常数λ=2.
评注:寻找点的坐标已经具有较高的开放性,同时还要求两条弦长的比值,因此本题的开放性更大,问题的求解需要具备较高的定力,需要探索问题的勇气和较高的理性思维.无论问题有多开放,用代数表示两条弦长的长度才是关键,在此过程中结合圆的性质.本题将本节课推向高潮.
2.是否存在这样的常数

(1)求椭圆C的标准方程;
(2)是否存在实数t,使得|AF1|+|BF1|=t|AF1||BF1|恒成立?若存在,求出t的值;若不存在,说明理由.



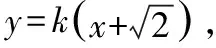


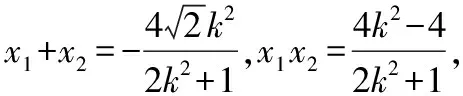
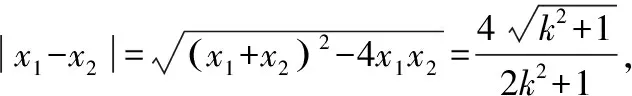




因为|AF1|+|BF1|=t|AF1||BF1|,
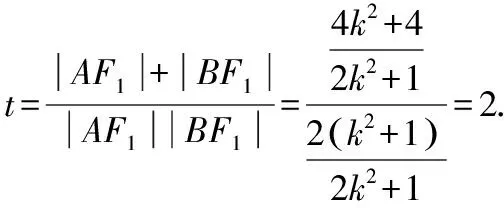
综上,存在实数t=2,使得|AF1|+|BF1|=t|AF1||BF1|恒成立.
评注:问题2切换问题情境,引入参数,设置“是否存在这样的常数”的问题,问题不仅有很高的开放性,还具有较强的灵活性,问题2的求解首先需要将问题转化,分类讨论,然后联立直线与曲线方程,进而进行一系列的运算推理,最后将问题解决.
3.是否存在这样的曲线
问题3及变式6与变式7都是以“是否存在这样的曲线”设置问题,问题具有高度的开放性、探索性和综合性,运算量并没有增加,但思维能力的要求大大提高,这几道试题对培育学生的数学灵魂——数学思维能力有积极意义.

(1)求C1,C2的方程;
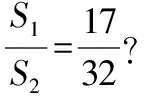


(2)①略;②设直线MA的斜率为k1,

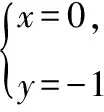


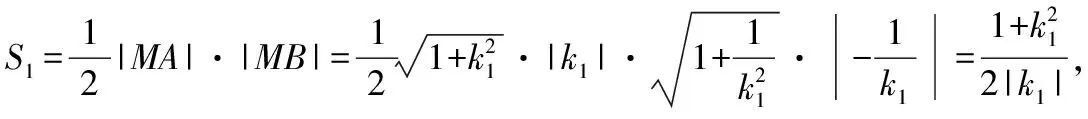

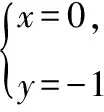
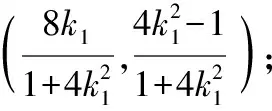




评注:由于本题中已知直线l经过定点(坐标原点),因此降低了难度,此时只需直线l的方程并根据题意列方程,求交点坐标,最后化简求出直线l的斜率k的值即可得出“存在这样的直线”的结论.
3.1 是否存在这样的圆

(1)求椭圆E的方程;
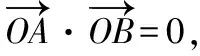

(2)当直线l斜率不存在时,设直线l的方程为x=n,

当直线l斜率存在时,设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),


Δ=16(4k2-m2+1)>0,


所以5m2-4k2-4=0, 5d2(1+k2)-4k2-4=0,恒成立,即(5d2-4)(k2+1)=0恒成立 ,
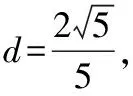
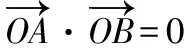
评注:本题主要考查圆的方程,由于圆心为坐标原点,因此要求圆的方程只需求圆的半径,根据题意列关于半径的方程,若方程有解则圆存在,若无解则圆不存在.该题主要考查函数与方程思想、化归与转化思想、分类讨论思想,考查推理论证能力、运算求解能力,求解时注意对直线的斜率分存在和不存在两种情况的讨论.
3.2 是否存在这样的抛物线
变式7:已知抛物线C的顶点在坐标原点,焦点在x轴上,P(2,0)为定点,若动圆M过点P,且圆心M在抛物线C上运动.点A,B是圆M与y轴的两交点,试推断:是否存在一条抛物线C,使|AB|为定值?若存在,求出这个定值;若不存在,说明理由.
【解析】设圆心M(a,b)(a≥0),点A(0,y1),B(0,y2).
因为圆M过点P(2,0),可设圆M的方程为(x-a)2+(y-b)2=(a-2)2+b2,
令x=0,得y2-2by+4a-4=0,所以y1+y2=2b,y1y2=4a-4,

设抛物线方程为y2=mx(m≠0),因为圆心M在抛物线C上,则b2=ma,
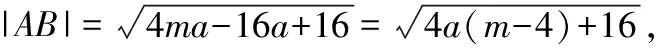
故存在一条抛物线y2=4x,使|AB|为定值4.
评注:本题涉及的问题较多,既有抛物线的存在性问题,又有线段的定值问题,具有较高的抽象性和综合性,问题的求解对学生的思维能力、分析和解决问题的能力要求比较高.本题的求解过程并不复杂,解答长度也不长,但很多学生找不到解决问题的切入口.解决本题首先根据题意设圆的方程和抛物线方程,再结合圆的性质和抛物线定义列相关方程,最后通过解方程解决问题.


