挖掘高考命题特点 奠定复习根基
陕西 韩红军 李朝阳
2022年高考全国乙卷理科数学秉承了考查数学关键能力、思维价值、核心素养的一贯设计理念,延续了以考查运算能力为主的传统,坚持熟而不俗,俗中有变,变而不偏,变中出新的原则,平凡问题中考查真功夫、真实情境中考查真能力.
1.试卷的特点分析与典型试题解析
1.1 密切联系社会,注重设置现实情境
今年高考密切联系社会,贴近生活,注重对数学基础知识、基本技能、基本数学思想方法、基本数学核心素养的全面考查.对基础知识的考查,并不要求学生死记硬背数学概念、公式和法则,而是注重考查学生对基础知识的理解和把握.例如,全国乙卷理科第4题以嫦娥二号卫星在完成探月任务后继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星为情境,考查学生综合应用数列、函数、不等式等基本知识,观察问题、分析问题和解决问题的能力.第19题以生态环境建设为背景,考查学生应用统计的基础知识和基本方法解决实际问题的能力,对数据处理与数学运算核心素养也做出了相应的考查.
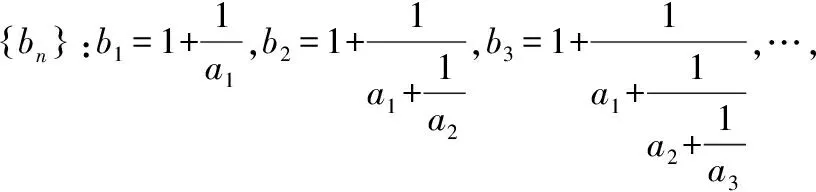
A.b1 试卷整体上保持一定比例的基础题,起点低,入手易,设置了一些源于教材又高于教材的试题,试图通过这一导向引导高中教师改变教学中过分依赖复习资料,脱离教材,迷信题海战术的情况.试题的考查内容范围和比例、要求层次与《普通高中数学课程标准(2017年版2020年修订)》(全文简称《课程标准》)保持一致,注重考查内容的全面性,同时突出主干、重点内容的考查,其中新教材淡化的线性规划、三视图和程序框图,仅考查了程序框图,体现了向新教材靠拢的趋势. 【例2】(2022·全国卷乙理·14)过四点(0,0),(4,0),(-1,1),(4,2)中的三点的一个圆的方程为. 【解析】设点A(0,0),B(4,0),C(-1,1),D(4,2),圆过其中三点共有四种情况,任意两点连接成的线段的中垂线的交点为圆心,圆心到任意一点的距离为半径,设圆的半径为r. (1)若圆过A,B,C三点,则圆心在直线x=2上, 设圆心坐标为(2,a),则4+a2=9+(a-1)2⟹a=3, 所以圆的方程为(x-2)2+(y-3)2=13; (2)若圆过A,B,D三点,则圆心在直线x=2上, 设圆心坐标为(2,a),则4+a2=4+(a-2)2⟹a=1, 所以圆的方程为(x-2)2+(y-1)2=5; (3)若圆过A,C,D三点, 则线段AC的中垂线的方程为y=x+1, 线段AD的中垂线的方程为y=-2x+5, (4)若圆过B,C,D三点, 则线段BD的中垂线的方程为y=1, 线段BC的中垂线的方程为y=5x-7, 高考数学创新试题形式引导教学更加注重核心素养和数学能力的培养,增强试题开放性,鼓励学生运用创造性、发散性思维分析问题和解决问题,引导教学注重培育学生的创新精神.例如,全国乙卷理科第10题打破平时常考古典概型和几何概型概率的计算,或是排列组合二项式定理的应用,而是考查独立随机事件概率的计算,并比较大小,也没有具体数值,增加了思维难度. 【例3】(2022·全国卷乙理·10)某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别是p1,p2,p3,且p3>p2>p1>0.记该棋手连胜两盘的概率为p,则( ) A.p与该棋手和甲、乙、丙的比赛次序无关 B.该棋手在第二盘与甲比赛,p最大 C.该棋手在第二盘与乙比赛,p最大 D.该棋手在第二盘与丙比赛,p最大 【解析】设该棋手在第二盘与甲比赛连赢两盘的概率为p甲,在第二盘与乙比赛连赢两盘的概率为p乙,在第二盘与丙比赛连赢两盘的概率为p丙,由题意得, p甲=p1[p2(1-p3)+p3(1-p2)]=p1p2+p1p3-2p1p2p3, p乙=p2[p1(1-p3)+p3(1-p1)]=p1p2+p2p3-2p1p2p3, p丙=p3[p1(1-p2)+p2(1-p1)]=p1p3+p2p3-2p1p2p3, 所以p丙-p甲=p2(p3-p1)>0,p丙-p乙=p1(p3-p2)>0,所以p丙最大,故选D. 注重通性通法在解题中的运用,都是运用基本概念分析问题,基本公式运算求解,基本定理推理论证,基本数学思想方法分析和解决问题.试题突出对学科基本概念、基本原理的考查,强调知识之间的内在联系,引导学生形成学科知识系统;注重本源性方法,淡化特殊技巧,强调对通性通法的深入理解和综合运用,促进学生将知识和方法内化为自身的知识结构. 【例4】(2022·全国卷乙理·17)记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A-B)=sinBsin(C-A). (1)证明:2a2=b2+c2; 【解析】(1)证明:因为sinCsin(A-B)=sinBsin(C-A), 所以sinCsinAcosB-sinCcosAsinB=sinBsinCcosA- sinBcosCsinA, 所以sinCsinAcosB+sinBcosCsinA=2sinBsinCcosA, 即sinAsin(B+C)=2sinBsinCcosA, 即sin2A=2sinBsinCcosA, 由正弦定理和余弦定理得, (2)因为a=5,所以b2+c2=50. 解得2bc=31, 所以△ABC的周长为a+b+c=5+9=14. 2022年试卷在保持难度适中的前提下,还注重考查学生的综合能力.在试题设置上,注重层次性,让不同能力水平的学生都能够得到充分的展示.试卷设计了思维较为深刻的问题,体现考生的能力水平.例如全国乙卷理科第9题研究球内四棱锥体积的最大值问题,要求学生有较强的空间想象能力和分析问题能力,将问题转化为三次函数的最值问题,进而利用导数求解. 【例5】(2022·全国卷乙理·9)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( ) 所以该四棱锥的体积 试题没有出现偏题怪题,考生解题所需方法也是平时训练中常用的方法,但试题命制没有落入俗套,要求考生具备坚实的数学基础、迅速准确的运算求解能力和灵活多变的解题方法.不少试题扎根于基础,然而,解题思路、方法等具备创新性. A.-21 B.-22 C.-23 D.-24 【解析】若y=g(x)的图象关于直线x=2对称, 则g(2-x)=g(2+x),因为f(x)+g(2-x)=5, 所以f(-x)+g(2+x)=5,故f(-x)=f(x), 所以f(x)为偶函数. 由g(2)=4,f(0)+g(2)=5,得f(0)=1. 由g(x)-f(x-4)=7,得g(2-x)=f(-x-2)+7, 代入f(x)+g(2-x)=5,得f(x)+f(-x-2)=-2, f(x)关于点(-1,-1)中心对称, 所以f(1)=f(-1)=-1. 由f(x)+f(-x-2)=-2,f(-x)=f(x), 得f(x)+f(x+2)=-2, 所以f(x+2)+f(x+4)=-2, 故f(x+4)=f(x),所以f(x)的周期为4. 由f(0)+f(2)=-2,得f(2)=-3, 又f(3)=f(-1)=f(1)=-1, 2022年全国乙卷理科命题归纳起来有“二十八字秘诀”:夯实基础考内功、关注思想强应用、提升能力重通法、升华素养追本真. 在复习备考时,以教材为本,对教材上的例题、知识点加以概括、提高和延伸,做到举一反三,达到触类旁通的效果.只有充分挖掘教材例、习题的功能,才能深刻理解教学内容的实质,挖掘教学内容内涵,实现质的突破.每年的高考数学试卷中,都有部分试题源于教材,高于教材. 全国乙卷理科对考生的计算与逻辑思维能力的要求有所提高,特别是客观题,常是两或三个知识点的综合交汇,每一步计算均需细心,要加强学生的运算求解能力,多角度去培养发展学生的逻辑思维能力.同时关注数学应用,关注身边科技发展中的大事、有意义的事、老百姓重视的事、社会反响大的事、能向社会传递正能量的事,关注数学史和数学文化,这些事情和历史文化都有可能与数学知识、数学思想方法结合起来命题. 高三数学复习过程中要针对主干知识、重点方法和主要数学思想进行突破,少做偏题与怪题.分析近五年的全国卷,概率与统计、立体几何、解析几何、函数与导数及不等式,依然是解答题考查的重点;解三角形和数列,轮换在解答题中出现.特别注意,全国卷对概率与统计的考查力度较大,全面考查概率与统计的基本思想和方法以及学生的综合能力和数学核心素养,充分体现了以核心知识为重点、以基本问题为载体、以现实生活为背景的交汇命题特点,平时教学中,要精心选择优质试题,深度挖掘试题的价值和功能,在试题变式、问法和拓展上下功夫,将学生“下题海”转变为教师“下题海”,优中选宝,题目针对性要强.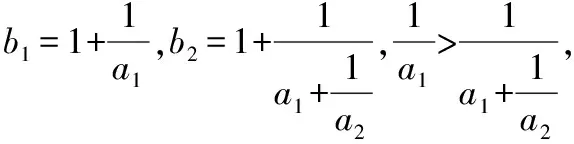
1.2 依据《课程标准》,注重考查主干知识和重点内容


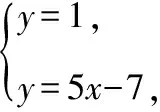

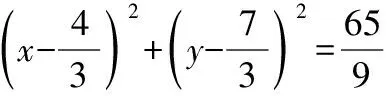
1.3 变中出新,注重创新试题的设计
1.4 立足教材,注重考查通性通法


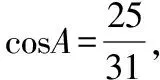

1.5 熟而不俗,注重考查思维的深度


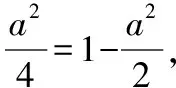
1.6 陈题变新,注重考查关键能力
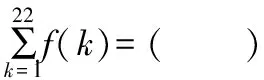
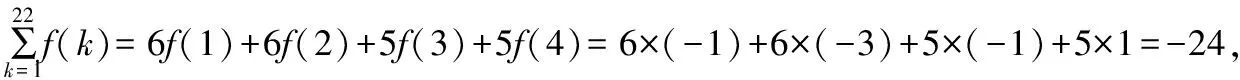
2.教学启示
2.1 注重回归教材,有效训练深度思维
2.2 关注数学实用性,大力培养关键能力
2.3 强化主干知识,体现“双减”落地
2.4 培养良好学习习惯,形成数学意识和核心素养


