基于能力素养培育的命题实践研究
——以“平面向量题命制的四种形式”为例
山东 刘目勇
解题和命题不仅仅是一个互逆的关系,更是一对相辅相成高效掌握数学核心知识的方法.教师的成长和学生核心素养的提高不能仅仅停留在解题的层次,而是需要换一种全新的角度,从命题的角度出发,洞察命题人的命题思路,解题就会事半功倍,对数学知识和方法的理解才会上升到一个比较高的层次.
在数学教学中,命题是一项重要而又艰难的工作,是一门技术,也是一门艺术.能够命制合格的试题乃至优秀的试卷,体现了一个教师的专业水平.很多情况下,我们遇到的大量题目,尤其是难题,常常属于会做,但却不知它是如何命制的,如果能够洞察命题人的想法,那么做起题来就能事半功倍.研究命题的角度和形式对于提升学生的数学核心素养起着至关重要的作用,所以在备考中教师要着力提升这一方面的研究.
命题的过程是一个反复琢磨的复杂过程,一道优秀的试题往往不是凭空捏造、从天而降,一般都会有题目的起源,可能是某种情境或某个核心概念,也可能是某道经典问题的拓展延伸.命题人通过“改编、类比、借鉴、原创”等多种形式找到题源,再利用“新旧结合”“移花接木”,甚至“推倒重建”等手段不断修改完善,最终才能命制出高质量的试题.本文将以高考压轴选择或填空题经常眷顾的平面向量内容为例,呈现几道试题反复研磨命制的过程,从四种常见形式来谈谈命题实践中的一些具体做法.
一、源于平面几何问题的改编
向量是数形结合的主阵地,很多向量问题都与平面几何图形有着千丝万缕的联系,只要学会了如何用向量语言描述几何图形,就能实现在代数向量与几何图形之间的自由切换.实际上,命题与解题恰好是一组互逆的操作,如果说我们在平时解题的过程中,习惯于通过翻译向量条件画出几何图形,那么命题的过程常常就是将几何图形用向量语言予以刻画.
【案例1】如图,在边长为1的正△ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上,则线段AD的最小值为________.


第1次命制:初步向量化
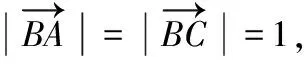

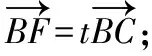


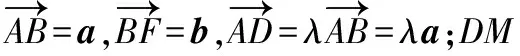





第2次命制:向量代数化

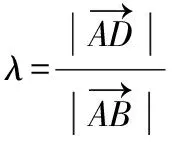




则点A在射线BA上运动,问题转化为求|OD|=λ的最小值,其中0<λ<1.
在△ABD中,|AD|=|OD|=λ,|BD|=1-λ,

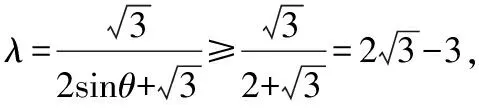
当且仅当sinθ=1,即AD⊥AB时取得最小值.

第3次命制:条件的等价代换

第4次命制:改变题型

A.有最小值,但无最大值
B.有最小值,也有最大值
C.无最小值,但有最大值
D.既无最小值,又无最大值
分析:作图后容易发现,当点A自点B向右移动时,点D也随之而动,显然当OA⊥OB时,CD∥OB,即λ→+∞,所以λ无最大值,但有最小值.这里,学生也可能会误以为当点A趋近于点B时,λ→0.5,选择题的题型存在误判风险.
二、源于核心考点的包装
【案例2】命题目标:借助极化恒等式解决的数量积问题.
第1步:如图,作长度为m的线段AB,并取中点D;
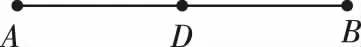


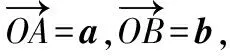

因为E点恰好为线段AB的四等分点(靠近点B),
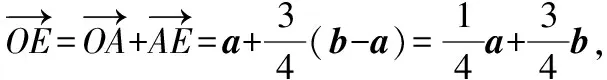
即(a-b)·(a+3b)=0.
第1次命制:为运算简便,令m=4
已知平面向量a,b满足|a-b|=4,(a-b)·(a+3b)=0,则a·b的最小值为________.
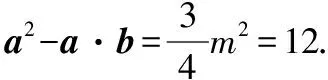
第2次命制:已知平面向量a,b满足|a-b|=4,a2-a·b=12,则a·b的最小值为________.
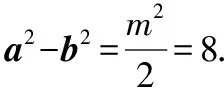
第3次命制:已知平面向量a,b满足|a-b|=4,a2-b2=8,则a·b的最小值为________.
点评:3次命制的试题异曲同工,都是源自于刻画垂线所得,如果教师或学生没有一定的经验,是很难想到它的源头的,解决问题时效率就会大打折扣甚至无法进行下去.命题和解题是一对 “冤家”,看不出源头也可以采取其他解决的办法,可以选择建立平面直角坐标系,设点解析化来解读条件,以a2-b2=8为例说明如下:
以AB的中点D为坐标原点,建立平面直角坐标系,设A(-2,0),B(2,0),O(x,y),则可得方程(x+2)2+y2-(x-2)2-y2=8,即x=1,由此确定点O在垂线l上运动.
建系设点是一种很好且常用的解题手段,但很难想象通过建系设点能命制出这一类型的平面向量题目,只会建系的人只是一个普通的解题者,真正懂向量语言的人才可能成为命题人.对于学生来说,学习平面向量的真正目的应该是掌握这一功能强大的语言,并可以熟练应用,这正是数学学习的真正能力及素养所在.
三、源于其他知识的类比
向量是一种具备丰富运算规律的运算对象,它与实数多项式的运算有许多异曲同工之处,所以将实数多项式的问题,改编成向量问题是一种比较常见的类比改编.
【案例3】设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是________.
命题思路:这个题目的解法多样且常见,如果将所有的实数x,y都改为向量a,b,会是一个什么样的局面呢?
第1次命制:已知平面向量a,b满足4a2+b2+a·b=1,则|2a+b|的最大值等于________.

因为4a2+b2≥4|a||b|≥4a·b,
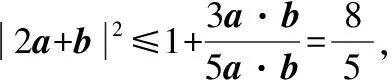
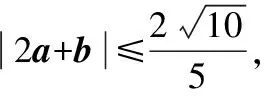
第2次命制:已知平面向量a,b满足4a2+b2+a·b=1,则|a+2b|的最大值等于________.
解:设a与b的夹角为θ,



当t=0时,|a+2b|2≤4,当t≠0时,
综上,当且仅当t=0,cosθ=1时,即a=0且|b|=1时,|a+2b|的最大值等于2.
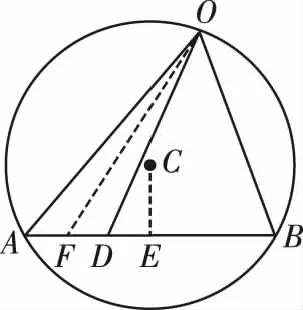
四、源于图形情境的构造
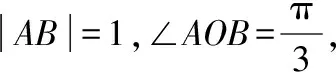







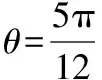

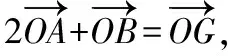

过圆心C作CE⊥AB于点E,
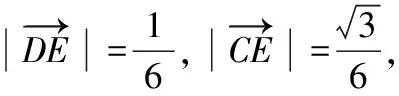




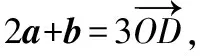
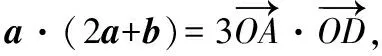

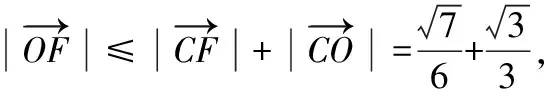
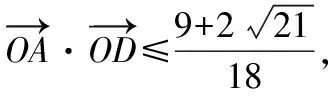
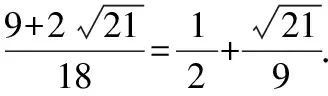
五、结束语

——四川美术学院雕塑系建系70周年文献展在重庆开幕

