精准设计 分类探究 层层变式 击破考点——三棱锥外接球微专题变式复习策略探究

广东 雷雄军 吴开震

外接球问题是培养学生直观想象和数学运算核心素养的一个非常好的载体，因此是高考命题的热点.纵观近五年的全国卷试题及各地模拟卷，球的知识大都以选择题和填空题的形式出现，综合考查空间想象能力和运算求解能力.在一轮、二轮的复习过程中，笔者发现学生对球的相关题目有种畏难心理，不能很好地作答，究其原因主要是学生对外接球问题的本质理解不清晰以及空间想象能力差等.因此笔者对此专题进行了一个微专题梳理复习.在整理近几年有关球的考题过程中，发现球的考题大多与三棱锥结合，考查三棱锥的外接球及其变式.因此笔者由2019年的高考真题出发，就三棱锥外接球知识展开了微专题复习，借助学生熟悉的长方体为背景层层变式，对三棱锥外接球考题从寻找球心位置这一本源角度出发进行了分类探究，通过例题及其层层变式，提升学生应对外接球考题的策略和能力.

一、母题的选取及分析

【母题】(2019·全国卷Ⅰ理·12)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E,F分别是PA,AB的中点，∠CEF=90°，则球O的体积为( )

【解析】如图1三棱锥P-ABC为正三棱锥，取AC的中点M，连接PM,BM，

则AC⊥PM，AC⊥BM，PM∩BM=M,可得AC⊥平面PBM，从而AC⊥PB，

又E,F分别是PA,AB的中点，所以PB∥EF.

因为∠CEF=90°,所以EF⊥CE，可得PB⊥CE，

又AC∩CE=C,所以PB⊥平面PAC，

图1

图2

此题在解答的过程中，由题目条件推导出侧棱两两垂直，进而转变为长方体的外接球问题，而长方体的体对角线为外接球的直径，因此很容易得到球心和半径.因为长方体有8个顶点，任选其中不共面的四个顶点构成的三棱锥，其外接球和长方体的外接球为同一个球.此类三棱锥外接球容易找到球心和半径.笔者以此题为契机，展开了对各种三棱锥外接球球心和半径的深入探究及其变式研究.

二、侧棱垂直底面的三棱锥外接球探究及相关变式

由于长方体有8个顶点，且侧棱和底面垂直，因此任意选取不共面的四个点可以构造出侧棱垂直于底面的三棱锥，此时其外接球与长方体为同一个外接球，直径为长方体的体对角线，球心为体对角线的中点.常见题型是侧棱垂直于底面，且底面是直角三角形.如图3、图4、图5所示.

图3

图4

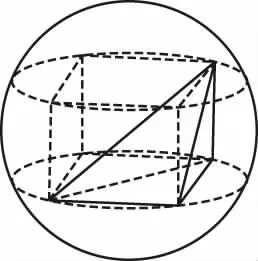
图5

【例题】《九章算术》中，将四个面均为直角三角形的三棱锥称为鳖臑，若三棱锥P-ABC为鳖臑，其中PA⊥平面ABC，PA=AB=BC=3,三棱锥P-ABC的四个顶点都在球O的球面上，则该球的体积是( )

【解析】如图6，该三棱锥有一条侧棱垂直于底面且底面是直角三角形，可以将四个顶点放入正方体中,且PC为体对角线，即为外接球的直径，中心为球心.

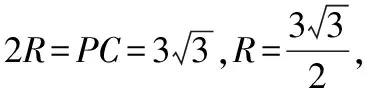
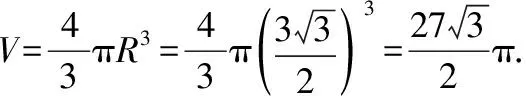
图6

图7

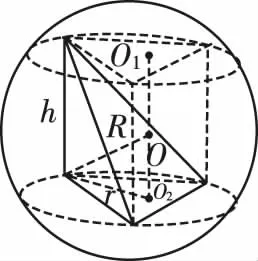
图8

图9

【解析】此题的三棱锥中侧棱PA⊥底面ABC，PA长度已知,按照上面的分析只需要求出底面外接圆的半径，由题意可知底面是等边三角形，因此外接圆的半径

三、正三棱锥外接球球心的探究及相关变式

正三棱锥作为一种特殊的三棱锥，其外接球问题也是常考问题，根据正三棱锥的定义，正三棱锥的四个顶点不可能为长方体的四个顶点.由于球心到底面三角形的三个顶点的距离相等，因此球心在正三棱锥的高上，如图10所示，半径可以在直角三角形AO1O中求解.

【例题】已知△ABC是边长为3的等边三角形，三棱锥P-ABC全部顶点都在表面积为16π的球O的球面上，则三棱锥P-ABC的体积的最大值为( )

图10

由于底面三角形的截面为一个圆，因此此种题型常见的变式为圆锥的外接球问题，球心及其半径的求法与正三棱锥一致.

设外接球半径为R，在Rt△OO1A中，

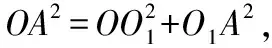
图11

四、正四面体外接球探究及相关变式

图12

【常见变式】此种类型题目常见的变式是考查完美四面体(即三组对棱两两相等的三棱锥)外接球问题，此时等同于对应长方体的外接球如图13所示，因此外接球的直径为体对角线，球心为体对角线中点.当然还可以变式为一组对棱相等，其余四条棱都相等的三棱锥外接球问题，等同于对应正四棱柱外接球如图14所示.

图13

图14

如图13设对应长方体的长、宽、高分别为a,b,c，

【解析】经过分析得知该四面体为完美四面体，由上面的分析可以得出直径

五、有两个侧面互相垂直的三棱锥外接球探究及相关变式

正方体中侧面和底面垂直，因此在侧面和底面中各取一个三角形可以组成有两个面互相垂直的三棱锥如图15所示.此题型的一般解法是先找两个互相垂直面的外心，然后过外心分别作面的垂线，两条垂线的交点就是三棱锥外接球的球心，如图16所示.

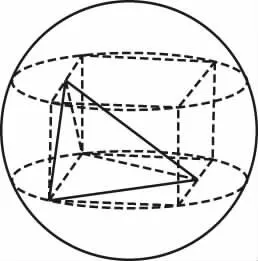
图15

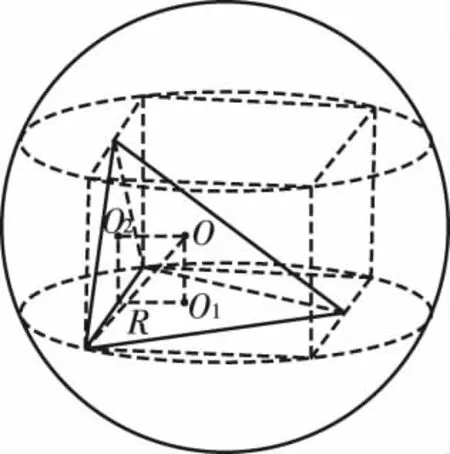
图16

【例题】已知三棱锥A-BCD中，△ABC是边长为2的等边三角形，DB⊥DA且平面DAB⊥平面ABC，则该三棱锥外接球的表面积为( ).

【解析】如图17所示，Rt△DAB的外心为斜边AB的中点O1，由于平面DAB⊥平面ABC，因此过O1且垂直平面DAB的直线为CO1，等边△ABC的外接圆圆心为O2，O2在CO1上，因此过O2作平面ABC的垂线与CO1交于点O2，即O2为球心，O2A为球的半径，所以

图17

【常见变式】此种题型常见的考查变式有以下两种：1.互相垂直的两个面都是特殊三角形如都为等边三角形，或者都为直角三角形等(见变式一)；2.两个垂直的面变成不垂直而是成一个特殊角如30°，60°或者120°等(见变式二、变式三).

【变式一】已知三棱锥D-ABC中，平面DAB⊥平面ABC，△ABC和△DAB均为边长为2的等边三角形，则该三棱锥外接球的表面积为________.

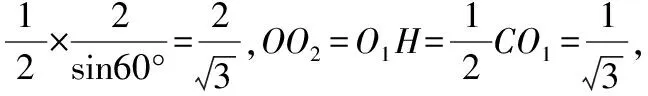
所以外接球半径

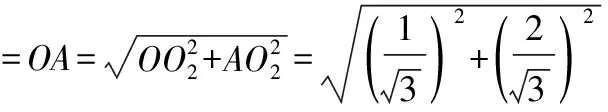
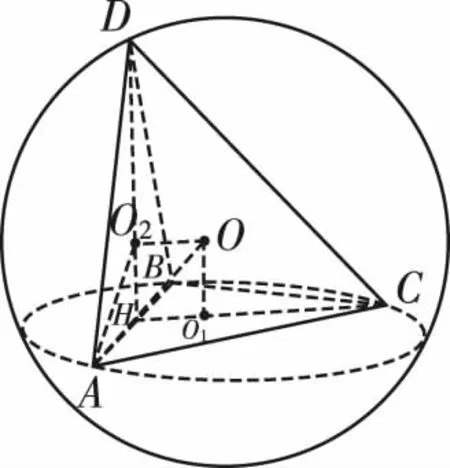
图18

取AC的中点D，连接BD和SD，

则∠SDB为二面角B-AC-S的平面角，即∠SDB=120°.

因为△ABC为直角三角形，因此D为△ABC的外心，

设△SAC的外心为O1，过点D作平面ABC的垂线，过点O1作平面SAC的垂线，则交点O为球心.

由已知得，∠SDO=30°，

在△SOD中,由余弦定理得，

SO2=OD2+SD2-2OD·SD·cos∠SDO，

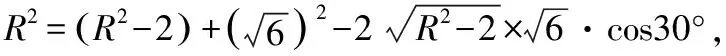
图19

如果上面变式二中的△SAC是以∠ASC为直角的直角三角形，这个时候不管二面角B-AC-S的大小为多少，斜边AC的中点到三棱锥四个顶点的距离相等，即AC的中点为球心.因此两个共斜边的直角三角形构成的三棱锥，其外接球的球心是公共斜边的中点.

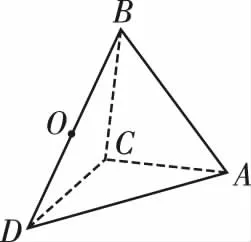
图20