取素养之势 明逻辑之道 优数理之术
——对一道模考导数压轴题的解法审视和优化
陕西 巨小鹏
导数压轴题具有综合性,对逻辑推理和数学运算都有着非常高的要求,近几年的高考导数压轴题思考方式具有普遍性但也颇具灵活性.通过审视课堂教学内容,反思什么才是我们需要去关注的核心问题,如何培养学生推理论证和运算求解能力?本文通过对一道高三月考导数压轴题的剖析,对数学逻辑推理和数学直观做了一题多解的阐述,对构造函数和解法计算进行优化,即以数学核心素养为导向,深刻理解逻辑推理之道及优化数理运算之术.
1.试题呈现
已知函数f(x)=aln(x-1)+x2+(a-2)x-a+1.
(1)讨论f(x)的单调性;
(2)若f(x)存在极值,且f(x)≥0在(1,+∞)上恒成立,求a的取值范围.
2.解法剖析
2.1 通性通法是法宝,数学直观是方向
史宁中教授说:“对于任何学科的教学,最终都应当把培养学生的学科直观作为重要的价值取向.”数学直观是我们解题的首选方向,借助图形通过直观建立思维架构,构建逻辑,形成思想理论,即始于直观,成于推理,终于理念.
解析:(1)方法一:由题意,函数f(x)=aln(x-1)+x2+(a-2)x-a+1,a∈R,
可得f(x)的定义域为(1,+∞),








令g(x)=2x2+(a-4)x+2.
令Δ=a(a-8)≤0,即当0≤a≤8时,f′(x)>0,f(x)在(1,+∞)上单调递增,则当a≥0时,f(x)在(1,+∞)上单调递增.当a<0时,方法同上.

①当a≥0时,2t2+at+a>0,即f′(t)>0,所以f(t)在(0,+∞)上是单调递增;
②当a<0时,令2t2+at+a=0,则Δ=a(a-8)>0,



综上所述,当a≥0时,f(x)在(1,+∞)上单调递增;



评注:方法一通过对二次函数对称轴分类讨论,但是极少有人想到,大多数人想到的是方法二,根据韦达定理判断,然而对a分类讨论a∈(0,8)和a∈(-∞,0)∪(8,+∞),没有检验导致分类错误,方法三通过换元,将函数简单化,分类讨论起来思路就比较清晰,所以换元是简化运算的一种极为重要的方法,不可小觑,这个在第二问中也有所体现;方法四对方法二稍微做了优化,分类讨论的思路也就更加清晰.作为大题第一问,往往都是常规考查,方法也会比较常规,考查函数单调性无非就是分析法、定义法或者求导函数法.
(2)方法一:由(1)可知,若f(x)存在极值,




则φ(t)在(0,+∞)上单调递减.
因为φ(1)=0,所以当t∈(0,1)时,φ(t)>0,h(t)在(0,1)上单调递增;当t∈(1,+∞)时,φ(t)<0,h(t)在(1,+∞)上单调递减,

评注:分离参数是求参数取值范围的常见方法,整体分离很常见,换元也大大降低了运算量.
2.2 调整方案,感受必要性探路的完美解答
G·波利亚在名著《怎样解题:数学思维的新方法》中写道:“当我们最后得到的解答既长又复杂时,我们很自然会怀疑是否还有某个比较简洁而少迂的解答:你能以不同的方式推导这个结果吗?你能一眼就看出来吗?然而即使我们已经成功地找到了一个满意的解答,我们仍然会对找到另一种解答感兴趣,正如我们希望通过两种不同的途径使我们确信一个理论结果的有效性.在有了一种证明后,我们还想找到另一种,就好像我们在看到一个物体以后,还希望触摸它.”“没有任何一个题目是彻底完成了的.总还有些事情可做,在经过充分的研究和洞察以后,我们可以将任何解题方法加以改进,而且无论如何,我们总可以深化我们对答案的理解.”除了数学直观解决问题,通过联想、猜测和预判在求实数取值范围问题中也显得尤为重要,平时讲题过程中培养学生“数感”,在细微处见真知,在“数感”中见逆向思维的奇妙变化,引领学生的思维朝逻辑终点探索,所以必要性探路是解题思维的一个方向.
(2)方法二:由(1)可知,若f(x)存在极值,则a<0.
令t=x-1>0则g(t)=alnt+t2+at,
因为f(x)≥0恒成立,当x=2 时,f(2)=a+1≥0.必有a≥-1,即-1≤a<0.
充分性证明如下:
因为lnt≤t-1 且a<0,所以alnt≥a(t-1),
即g(t)=alnt+t2+at≥t2+2at-a,
此时Δ=4a(a+1)≤0,即-1≤a≤0,
所以当-1≤a<0时,g(t)≥0成立,符合题意.
方法三:充分性证明如下:
因为lnt≤t-1 ,则g(t)=-a(t-lnt-1)+t2+2at-a=-a(t-lnt-1)+(t+a)2-a(a+1)≥0,所以a的取值范围为[-1,0).
方法四:充分性证明如下:

可知g′(-a)=-a-1<0,g′(1)=2a+2>0.
则有t0∈(-a,1]使得g′(t0)=0,


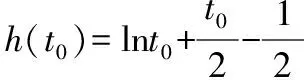
评注:必要性探路法,必要性很简单,证明充分性角度稍有不同,必要性探路是一种很重要的思想方法,让必要性和充分性完美结合,完成充要的合理解答,但是需要强大的数学基础和逻辑推理做支撑,难点在于如何确定取值.
2.3 算思结合,利用隐零点优化解题思路和运算方法
罗增儒教授说过:“解一道题忘一道题,或在同一思维层次上重复做好几道题,并不能获得解题能力的提高.注重解题过程的分析与改进,就是力图通过解‘有限道题’来获取‘无限道题’的那种教学机智.”他还说:“信息交合就是抓住整体分解中提炼出来的本质步骤,将信息单元转换或重组成新的信息块,这些新信息块的有序化将删去多余的思维回路,将用更一般的原理去集中现存的许多过程,将用一个简单的技巧去替代现有的常规步骤.于是,一个新的解法诞生了.”在解题中,设而不求也是一种解题策略,其优点是将信息交合,简化运算过程,解决核心问题,特别是利用导数求解过程中,隐零点法是解题的另一个方向.





解得-1≤a<0.





因为h(2)=1-1=0,所以x0∈(1,2],所以g(1)=a<0,g(2)=2a+2≥0,得a≥-1,解得-1≤a<0.


评注:由于方法四的启示,方法五六不用必要性探路,利用隐零点也可以进行处理,大大简化了计算,方法七进行了优化处理,思路也更加明晰.
3.结束语


