立足单元教学设计 培养纠错思维品质

甘肃 张建文

单元教学是促使数学核心素养落地生根的重要手段，数学单元教学的设计要体现出整体关联性、动态发展性和团队合作性，而教学主题的选择通常有知识类主题、方法类主题和素养类主题.其中方法类主题既有观念层面的也有操作层面的，本文尝试从培养学生良好学习习惯的角度来探索方法类主题的教学模式.主要从六个角度梳理学生常见的思维误区，分析产生思维误区的原因，纠正解答错误，并进行变式提升训练或拓展延伸训练，同时提供切实可行的教学建议.通过研究经典实例，将学生常见的思维误区直观化、具体化和可视化，经过探究错解后面所隐含的思维误区，纠正思维习惯，培养良好的思维品质，从而更好地强化“四基”，提高“四能”，促进学生理性地思考问题，使得学生会学习爱学习，从中享受到学习的快乐，进而达到培养数学核心素养的目的.

1.运算素养待提高，特殊位置难处理

数学运算是训练考生逻辑推理的重要途径，要求在熟悉运算对象的基础上，根据数学对象的结构特点和形式特征，选择恰当的方法进行变形化简.运算的正确、有据、合理、简洁是运算能力的主要特征.在实际运算过程中，要善于分析运算条件，多角度尝试运算方向，选择恰当的运算方法，设计合理而简洁的运算程序等.在课堂教学过程中，要引导考生从单向思维到逆向思维和多向思维转变，引导考生在观察的基础上“看”出运算思路.若运算能力不足，就会出现“会而不对，对而不全”的问题，或是在某个转化位置上出现偏差.

(1)当3-a≤0即a≥3时，g(x)≤0，f′(x)≤0，所以f(x)在(0，+∞)上单调递减.

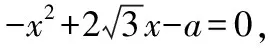
正确解答：由于(1)的解答完全正确，所以只需要纠正(2)即可.

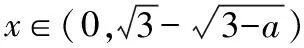
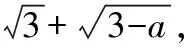
分析解答：由于解答前半部分与例1解题思路完全一致，所以从(2)开始：

2.直观思维有欠缺，绘图粗糙不到位

直观想象作为六大核心素养之一，整合了空间想象、几何直观和空间观念，是发现和提出问题、分析和解决问题的重要手段.在能力层面，要求考生能够准确作图进而利用数形结合思想解决数学问题，依托图形理解数学本质.在实际教学中，教师要引导考生能够“遇数想形，见形转式”，帮助考生形成较好的数学直观思想.若直观思维欠缺，就会出现绘图不规范、不准确，看图有偏差，进而做题出错，素养难以提升.

【例2】已知函数f(x)=|lgx|-kx-2，给出下列四个结论，其中正确的结论是( )

A.若k=0，则f(x)有两个零点

B.∃k<0，使得f(x)有一个零点

C.∃k<0，使得f(x)有三个零点

D.∃k>0，使得f(x)有三个零点

错误呈现：若∃k<0，使得f(x)有一个零点，则存在的零点为x=1.

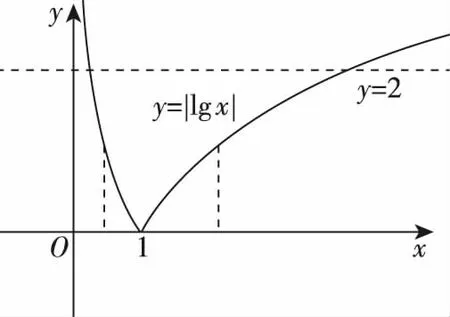
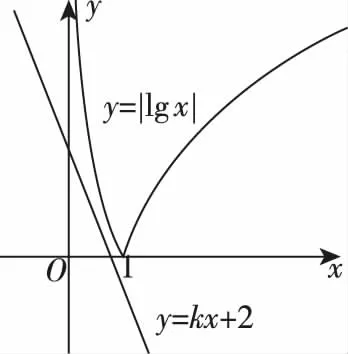
f(x)=|lgx|-kx-2的零点⟺方程|lgx|-kx-2=0的根⟺方程|lgx|=kx+2的根⟺函数y=|lgx|与y=kx+2图象的交点，绘制y=|lgx|与y=kx+2(k<0)的图象如图，由图可知，所以∃k<0，使得两函数图象的交点为(1，0)，即f(x)有一个零点为x=1.故选B.

错因分析：考生对函数图象的认识不准确不到位，平时作图太随意，对函数图象的变化快慢掌握不到位.在研究函数单调性的时候，能够依图说明问题，但是涉及两条曲线的相对位置关系或函数变化快慢的时候，考生就容易出现错误.

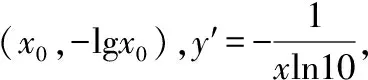
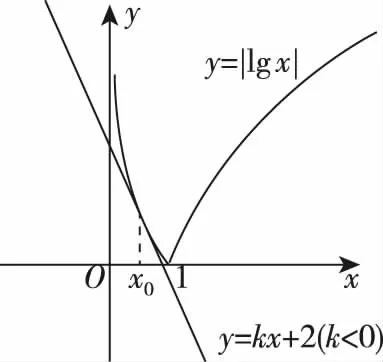
所以∃k<0，使得f(x)只有一个零点为x0，故选B.

拓展提升：探究直线y=kx+2在转动过程中与曲线y=|lgx|的交点情况：

(1)直线y=kx+2过定点(0，2)，下面探究当直线斜率k变化对两函数图象交点的影响.

①探究y=kx+2与y=|lgx|相切的临界状态.

如图，当y=kx+2与y=lgx(x>1)相切时：

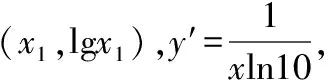
又由于切线过点(0，2)，

所以在k变化的过程中有如下结论：

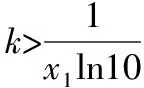
如图，当k=0时，y=kx+2与y=|lgx|图象有两个交点，函数f(x)有两个零点.

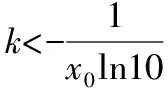
3.通性通法不熟练，以偏概全出偏差

通性通法主要是指具有某些规律性和普遍意义的常规解题模式和常用的数学思想方法.通性主要指数学概念所反应的数学基本性质，通法主要指数学概念所蕴含的数学思想方法.在教学中，教师要引导考生深入理解数学概念的本质，总结并掌握研究数学对象的一般性方法和思路.例如在最值求解过程中，通常是从函数视角去分析解答，而且研究函数的一般性思路是：定义域→图象→性质，或是定义域→性质1→图象→性质2.如果考生对研究对象的通性通法不熟练，就会出现以偏概全的错误.

【例3】下列表述正确的是( )

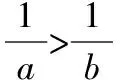
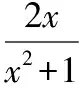
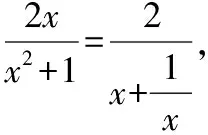
错因分析：运算错误，在表达式变形的时候考虑不全面，缺少表达式变形的一般性思维，忽略运算规则的特殊要求，进而出现以偏概全，只考虑到x取值的一个侧面，并没有全面考虑问题.从中可以看出“四基”中的基本技能欠缺，缺乏函数思想.函数思想是解决最值问题或取值范围问题的常用手段，从函数角度入手可以极大地简化问题.在此错例中，从考生思维角度来讲，由于缺失解决问题的通性通法导致错误出现.

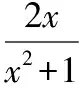
拓展提升：立足课标要求，从考生的能力发展角度设计探究活动.

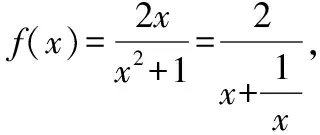
据此可得f(x)在[0，+∞)上的图象，再根据奇偶性，引导考生得到f(x)的整条图象如图，进而得到函数f(x)在R上的其他性质.

4.求解过程不合理，条件转化不等价

数学问题的解答不但要求有明晰的思路，而且要求有规范且合乎逻辑的过程.合理的解答过程能够体现出由条件到结论的流畅性与自然性，是对题目条件的等价化简后所呈现出来的最简洁的形式.在解题教学中，需要师生共同探究问题解决的基本思路，然后进行有理有据的过程书写，最后对得出的结果进行验证，如果必要可以对解答过程进行回顾总结.这个求解过程缺一不可，是形成考生良好问题解答思维习惯的必经之路，如若缺失，就会出现解答结果看似合理规范，但实际结果错误的情形.

即ω=1+2k，k∈N③，

由③④可得ω的最大值为11.

错因分析：这题是三角函数中求参数范围的经典实例，由①②推理得出③的过程中题目原始含义已经发生变化，其实①②是③的充分不必要条件，并不是等价条件，这样导致得出的结论错误.所以在解题过程中一定要确保条件的转化是等价的，若不等价一定要将所得结果进行验证以满足原始条件.

正确解答：由上可知，ω=1+2k，k∈N且ω≤12，即ω=1，3，5，7，9，11.

(1)当ω=11时，f(x)=sin(11x+φ)，下面验证是否满足零点和对称轴要求.

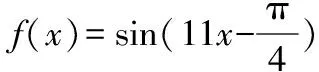
(2)当ω=9时，f(x)=sin(9x+φ)，下面验证是否满足零点和对称轴要求.

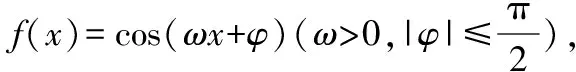
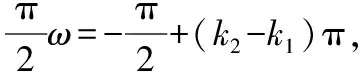
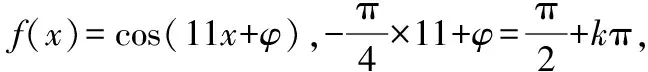
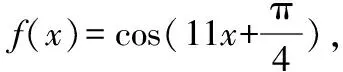
综上可知，ω的最大值为9.

5.审题维度太单一，隐含关系看不出

数学审题就是在明确问题要求的基础上，通过准确分析题目条件的含义，对条件进行等价化简，寻找条件与问题要求的差距，并形成由条件转化成问题答案的基本思路.审题的关键在于对题目条件的准确理解和合理转化，多维度多层次分析题目条件所表现出来的显性条件和隐性条件，挖掘变量之间的各种关系并进行恰当转化.在教学过程中，数学审题要求学生眼到、手到、心到，需要考生多维度去思考解决问题的多种可能性，引导考生“看出”数学思路，并选择最简洁最高效的方法.如若审题出现问题，就会使得条件分析不全面而出现错误.

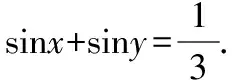
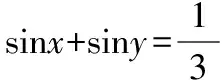
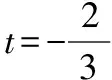
6.整体视角不宽广，机械模仿出错误

数学知识的理解深度决定其应用的灵活度，对数学概念的深度理解就要理解知识的上下位关系、与其他知识的纵横联系、在数学知识结构中的作用与价值、知识产生的逻辑背景、知识所能解决的数学问题等等，要达到这样的理解程度，就需要有整体观念，从整体视角去看待知识的来龙去脉，理解整体与部分之间的逻辑关系.在教学过程中，教师要引导考生观察表达式结构，深刻理解知识的本质，区分不同知识在表达和呈现形式上的异同.如若整体视角不够宽广，就会对知识的本质理解不到位，进而在知识的应用时出现机械模仿或答非所问的情况.

【例6】已知函数f(x)=ax2+bx，且1≤f(-1)≤2，2≤f(1)≤4，求f(-2)的取值范围.

错误呈现：由于1≤f(-1)≤2，2≤f(1)≤4所以1≤a-b≤2 ①；2≤a+b≤4 ②.

所以4≤4a-2b≤11，即f(-2)的取值范围是[4，11].

错因分析：在多次使用不等式的同向相加性质时，等号成立的条件可能不同，从而造成累计误差，最终使得不等式的取值范围扩大.从本质上讲，考生对运算对象的结构特点和组成方式不太理解，观察不够细致，对不等式性质的使用规则机械仿照，更深层次地体现出学习方法的不科学和对数学知识本质把握的不准确.

正确解答：已知1≤a-b≤2，2≤a+b≤4，

令4a-2b=x(a-b)+y(a+b)=(x+y)a+(y-x)b，

即4a-2b=3(a-b)+(a+b)，3≤3(a-b)≤6，2≤a+b≤4，

所以5≤3(a-b)+(a+b)≤10，

故而f(-2)的取值范围是[5，10].

变式提升：已知-2≤x+y≤1且0≤2x-y≤3，求x-y的取值范围.

解析：令x-y=m(x+y)+n(2x-y)=(m+2n)x+(m-n)y，