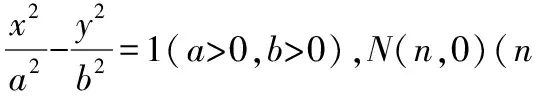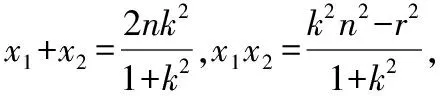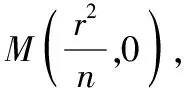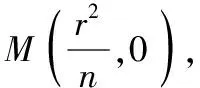在探究中溯源 在变式中求真
——以一道典型圆锥曲线问题为例
江西 邹荣华 颜 琴
圆锥曲线在高考及模拟考试中经常考查对称问题、面积问题、定值问题、定点问题以及向量问题、存在性问题、探究性问题等,本文以一道典型圆锥曲线问题为例,通过多角度思考,以问题为驱动,不断探究,一题多变,以点带面,涉及圆锥曲线中以上列举出的各种问题.

(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.

【分析】要证明∠OMA=∠OMB,通过直线AM,BM斜率之和为零建立方程进行求证.

(2)当l与x轴重合时,∠OMA=∠OMB=0°;
当l与x轴垂直时,OM为AB的垂直平分线,所以∠OMA=∠OMB;
当l与x轴不重合也不垂直时,
设l的方程为y=k(x-1)(k≠0),


得(2k2+1)x2-4k2x+2k2-2=0,
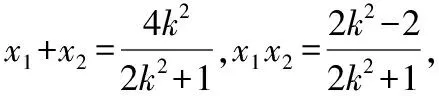
Δ=16k4-4(2k2+1)(2k2-2)=8(k2+1)>0,

由y1=kx1-k,y2=kx2-k得,

所以kMA+kMB=0,故直线MA,MB的倾斜角互补,所以∠OMA=∠OMB;
综上,∠OMA=∠OMB.
一、结论变换
变式一:当l与x轴不重合时,证明:MO平分∠AMB;
【分析】由∠OMA=∠OMB易得MO平分∠AMB.
变式二:当l与x轴不重合时,证明:直线MA,MB的倾斜角互补;
【分析】由原题解法中kMA+kMB=0可得直线MA,MB的倾斜角互补.
变式三:当l与x轴不重合时,证明:点F到直线MA,MB的距离相等;
【分析】因为F在∠AMB角平分线MO上,所以F到直线MA,MB的距离相等.
变式四:当l与x轴不重合时,证明:A关于x轴对称点A′ 在直线BM上;
【分析】方法1:由原题∠OMA=∠OMB易得MO平分∠AMB,又因为直线MO即为x轴,易知A关于x轴对称点A′ 在直线BM上;
方法2:利用向量证明B,A′,M三点共线,得到点A′在直线BM上.
证明:当l与x轴垂直时,A′与B重合,易得点A′在直线BM上;
当l与x轴不垂直时,设l的方程为y=k(x-1)(k≠0),
A(x1,y1),B(x2,y2),A′(x1,-y1),


(2k2+1)x2-4k2x+2k2-2=0,
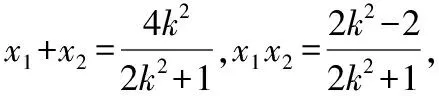
Δ=16k4-4(2k2+1)(2k2-2)=8(k2+1)>0,
要证A关于x轴对称点A′ 在直线BM上,

即证(x1-2)y2+(x2-2)y1
=(x1-2)(kx2-k)+(x2-2)(kx1-k)
=k[2x1x2-3(x1+x2)+4]
=0.

综上,点A′在直线BM上.
变式五:当l与x轴不重合时,证明:|AM|·|BF|=|AF|·|BM|;

变式六:当l与x轴不重合时,证明:|BM|·S△AMF=|AM|·S△BMF;
【分析】由F到直线MA,MB的距离相等,并设为d,

得|BM|·S△AMF=|AM|·S△BMF


变式八:kMA+kMB是否为定值?若是求出定值,若不是说明理由;
【分析】由原题解法易得kMA+kMB=0,故kMA+kMB定值为0.
变式九:能否求出kAM·kBM的取值范围?
【分析】由原题解法得到kAM·kBM关于k的函数式,再求出范围.
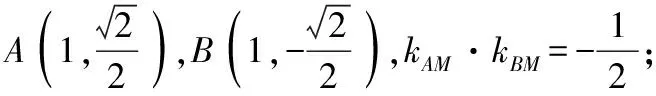
当l与x轴不垂直时,设l的方程为y=k(x-1),


得(2k2+1)x2-4k2x+2k2-2=0.
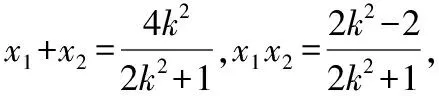
Δ=16k4-4(2k2+1)(2k2-2)=8(k2+1)>0,

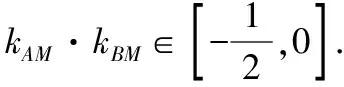



二、逆向变换
将题目已知中的“点M的坐标为(2,0)”去掉,把结论放入已知,从多个角度进行逆向设问,寻找点M是否存在.

【分析】假设M存在并设M(m,0),根据∠OMA=∠OMB用kAM+kBM=0列式求解m,再作出判断.
解析:假设M存在并设M(m,0),
当l与x轴不垂直时,设l的方程为y=k(x-1),


得(2k2+1)x2-4k2x+2k2-2=0,
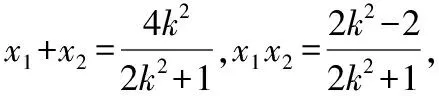
Δ=16k4-4(2k2+1)(2k2-2)=8(k2+1)>0,
因为∠OMA=∠OMB,所以kAM+kBM=0,

因为k不恒为0,

当l与x轴垂直时,易得M(2,0),满足∠OMA=∠OMB;
综上,存在M(2,0),使∠OMA=∠OMB恒成立.

【分析】假设M存在并设M(m,0),
由BMS△AMF=|AM|S△BMF,得
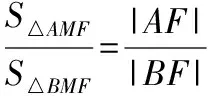
可知F在∠AMB的平分线上,由kAM+kBM=0建立方程求解m.



理由如下:设存在符合题意的点M(m,0),则:
当直线AB的斜率存在时,设l的方程为y=k(x-1),


得(2k2+1)x2-4k2x+2k2-2=0.
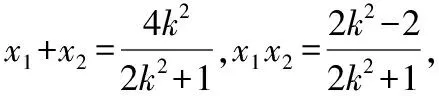
Δ=16k4-4(2k2+1)(2k2-2)=8(k2+1)>0,
y1y2=k2(x1-1)(x2-1)
=k2[x1x2-(x1+x2)+1]

=x1x2-m(x1+x2)+m2+y1y2





逆向变换是把原命题的结论作为已知,去探究使之满足的其他条件.变式一至变式十(变式九除外)都可以这样逆向设置问法进行逆向变换,其他具体变换略.逆向变换是思维的逆向过程,难度较大,常常是存在性问题、探究性问题的命制方式,比如变式十二,这样设置问题,不仅题目新颖,而且难度变大.
三、综合变换
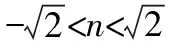

【分析】类比变式十一的解法,
解析:假设M存在并设M(m,0),
当l与x轴不垂直时,设l的方程为y=k(x-n),


得(2k2+1)x2-4nk2x+2n2k2-2=0,

Δ=16n2k4-4(2k2+1)(2n2k2-2)=8(2k2-n2k2+1)>0,
因为∠OMA=∠OMB,所以kAM+kBM=0,

因为k不恒为0,

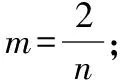



【分析】类比变式十一的解法,
解析:假设M存在并设M(m,0),
当l与x轴不垂直时,设l的方程为y=k(x-c),
A(x1,y1),B(x2,y2),则|x1| 得(a2k2+b2)x2-2a2ck2x+a2c2k2-a2b2=0, Δ=4a4c2k4-4(a2k2+b2)(a2c2k2-a2b2)=4a2b2(a2k2+b2-c2k2)>0, 因为∠OMA=∠OMB,所以kAM+kBM=0, 因为k不恒为0, 【分析】类比变式十五的解法, 解析:假设M存在并设M(m,0), 当l与x轴不垂直时,设l的方程为y=k(x-n), A(x1,y1),B(x2,y2),则|x1| 得(a2k2+b2)x2-2a2nk2x+a2n2k2-a2b2=0 Δ=4a4n2k4-4(a2k2+b2)(a2n2k2-a2b2)=4a2b2(a2k2+b2-n2k2)>0, 因为∠OMA=∠OMB,所以kAM+kBM=0, 因为k不恒为0, 变式十七:题中椭圆变为双曲线,是否有类似结论? 【分析】类比变式十六的解法, 解析:假设M存在并设M(m,0), 当l与x轴不垂直时,设l的方程为y=k(x-n), A(x1,y1),B(x2,y2),则|x1|>a, |x2|>a, 得(b2-a2k2)x2+2a2nk2x-a2n2k2-a2b2=0, Δ=4a4n2k4-4(-a2k2+b2)(-a2n2k2-a2b2)=4a2b2(n2k2+b2-a2k2)>0 因为∠OMA=∠OMB,所以kAM+kBM=0, 因为k不恒为0,所以, 变式十八:题中椭圆变为抛物线,是否有类似结论? 抛物线C的方程为:y2=2px(p>0),N(n,0)(n为已知且n>0), 过N的直线l与C交于A,B两点,当l与x轴不重合时,x轴上是否存在定点M,使∠OMA=∠OMB恒成立,若存在求出定点,若不存在说明理由; 【分析】类比变式十六的解法, 解析:假设M存在并设M(m,0), 当l与x轴不垂直时,设l的方程为y=k(x-n), A(x1,y1),B(x2,y2),则x1>0 ,x2>0 , 将y=k(x-n)代入y2=2px, 得k2x2-(2nk2+2p)x+k2n2=0, Δ=(2nk2+2p)2-4n2k4=4p(2nk2+p)>0, 因为∠OMA=∠OMB,所以kAM+kBM=0, 因为k不恒为0, 解得m=-n; 当l与x轴垂直时,易得M(-n,0),满足∠OMA=∠OMB; 综上,存在M(-n,0),使得∠OMA=∠OMB. 变式十九:题中椭圆变为圆,是否有类似结论? 圆C的方程为:x2+y2=r2(r>0),N(n,0)(n为已知,-r 【分析】类比变式十六的解法, 解析:假设M存在并设M(m,0), 当l与x轴不垂直时,设l的方程为y=k(x-n), A(x1,y1),B(x2,y2),则-r 将y=k(x-n)代入x2+y2=r2, 得(1+k2)x2-2nk2x+k2n2-r2=0, Δ=4n2k4-4(1+k2)(k2n2-r2)=4(k2r2+r2-k2n2)>0, 因为∠OMA=∠OMB,所以kAM+kBM=0, 因为k不恒为0, 同类变换是数学中常见的同类型中由一类成立,联想到另一类或几类是否也成立,从而进行变换设问的一种方式,这是数学中重要的类比推理的思想.比如上面的同类变换由椭圆中的结论成立,分别变换成双曲线、抛物线和圆中此结论是否也成立,这种从一类到另一类的探究过程,使我们由懂一类题到通一片题.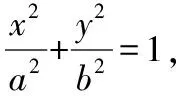

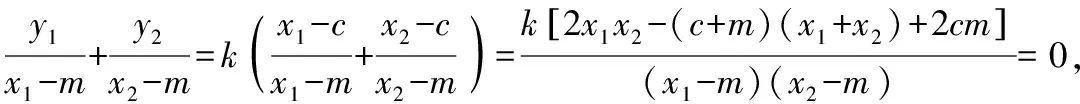




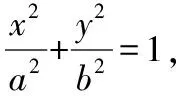
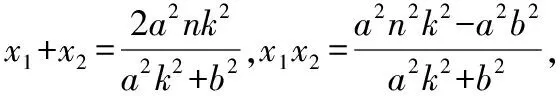


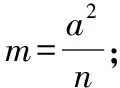



四、同类变换