一种基于改进型k-means 聚类算法的退役电池组筛选重组方法

程阳阳

（上海理工大学 机械工程学院，上海200093）

0 引 言

近年来，在国家政策支持、地方政府补贴以及动力电池技术不断升级下，我国新能源汽车得以快速发展，而随着电动汽车保有量的逐渐增加，伴随而来的是动力电池退役浪潮，预计2025 动力电池退役量将超过90 GWh［1-2］。 电池组的性能并不是简单的电池单体按比例放大，由于组内单体间的差异性，单体成组之后存在“木桶效应”，即电池系统的性能取决于性能最差的单体，这就导致了电池组内某个或某些单体达到退役寿命时即容量衰减至初始容量的80%，电池组内其他单体还有80%以上的初始容量可以利用，而且那些达到退役寿命的电池同样具备潜在的利用价值。 如果将这些电池进行有效分选、重组，那么动力电池的残余容量可以继续用于其他性能要求较低的应用领域，如用于低速电动二轮车或者储能电站等领域，这便是对退役电池组的梯次利用［3］。

电池系统的使用性能和安全性无疑取决于每个电池单体的固有性能。 而且动力电池组在实际使用过程中，电池之间的差异性可能是自放电率、容量、SOC、内阻等多因素耦合共同作用导致，诸多的不一致性造成了电池组整体的使用寿命和安全性能急剧恶化［4］。 本文将从电池单体容量、电量、内阻三个维度出发，建立电池组状态特征矩阵。 并且针对电池组内单体状态差异性提出了一种改进型k-means聚类方法实现退役电池组的重组，即认为单体的容量、电量、内阻每个维度上的差异对电池组整体不一致性的影响程度不同，进而利用信息熵理论确定每个维度的权重，也就是对k-means算法中不同维度的距离度量公式乘上权重系数。 基于聚类后的结果，提出了退役电池组可能的应用场景。 进一步，基于实验数据分析重组后的电池模块的电压一致性，结果表明这种方法可以有效筛选出一致性较高的电池单体。 本研究可以最大化挖掘动力电池组的价值，完善电池组全生命周期的价值链。

1 退役电池组重组方法

1.1 改进型k-means聚类方法

电池组的不一致性的表征参数包括容量不一致性、SOC不一致性、内阻不一致性等，上述不一致性参数之间相互耦合且对电池组整体不一致性影响程度不同。 考虑到电池组的不同用途，尤其是退役电池组筛选重组后不同的应用场景，对电池组内单体各性能的一致性要求不同。 对于能量型应用场景，人们更关心的是电池模组的能量储存能力以及持续放电能力，因此对单体间容量的一致性要求较高。 对于功率型应用场景，人们更关心的是电池模组的功率输出能力和脉冲充放电能力，因此对单体间内阻的一致性要求较高。 而电池模组内单体间的SOC一致性较高，可以有效提高模组的能量利用效率。 因此本文以电池单体的容量、SOC、内阻作为退役动力电池组筛选重组的评估指标。

k-means算法是一种非常典型的基于欧氏距离的聚类算法，不同个体之间采用欧氏距离作为相似性的评价指标，即认为在空间距离中越近的个体其相似度越大［5-8］。 通过k-means聚类算法可以把性能相近的电池单体分配到一个簇内，以便提高重组后电池模组的一致性，对于有效延长电池组使用寿命并保证电池工作的安全性是非常必要的［9］。 传统的k-means聚类算法认为在欧式空间中每个维度对于整体的影响效果是相同的，而为了解决退役电池组众多不一致性参数相互耦合的问题，提出了一种改进型k-means聚类算法，即认为单体的容量、电量、内阻每个维度上的差异对电池组整体不一致性的影响程度不同，进而利用信息熵理论确定每个维度的权重，也就是对kmeans算法中不同维度的距离度量公式乘上权重系数。

本文中我们将基于改进型k-means聚类算法的退役电池组筛选重组分为两个阶段。

阶段一：退役电池组特征矩阵的建立以及数据标准化。 假设电池组内电芯数量为n，选择的评价因子数量为m。 则评价系统的原始数据矩阵X如式（1）所示。

式中：xij表示对应于第i个电芯的第j个评估因子。

由于每个评价因子的维度不同，需要对原始矩阵进行归一化处理，得到所有评价因子的归一化矩阵。 在对原始数据矩阵进行归一化的过程中，容量等正评价因子越大，结果越好。 而内阻等负面评价因素越小，效果越好。

正类评价因子的归一化公式为：

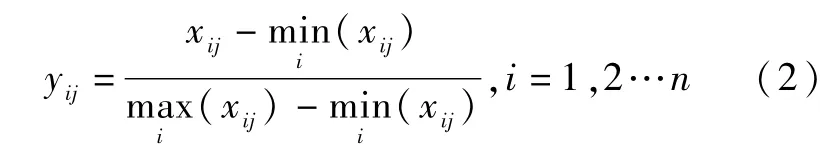
负类评价因子的归一化公式为：

最终可以得到所有评价因子的归一化矩阵Y：

阶段二：聚类。 依据聚类原理可以将聚类过程分为以下几个步骤。

步骤1：设置聚类的类簇个数为k，最大迭代次数为N，迭代终止阈值为δ。

步骤2：从数据集X中随机选取k个样本作为初始聚类中心：B=｛u1，u2，…，uk｝，其中uk=［uk，c，uk，soc，uk，r］。

步骤3：根据距离度量公式计算每个样本xi与聚类中心ujuj的欧氏距离dijdij，距离计算公式如式（5），并把每个样本分配到与该样本距离最近的簇内，定义输出的分类集合为C=｛C1，C2，…，Ck｝。

式中：w为利用熵权法根据每个评价因子对电池组整体不一致性影响程度得到的权重。

步骤4：更新聚类中心。 对于j=1，2，…，kj=1，2，…，k，根据下式计算新的聚类中心：

步骤5：重复上述迭代过程，直到聚类中心不再发生改变或者达到最大迭代次数停止迭代。

步骤6：输出最终分类结果。

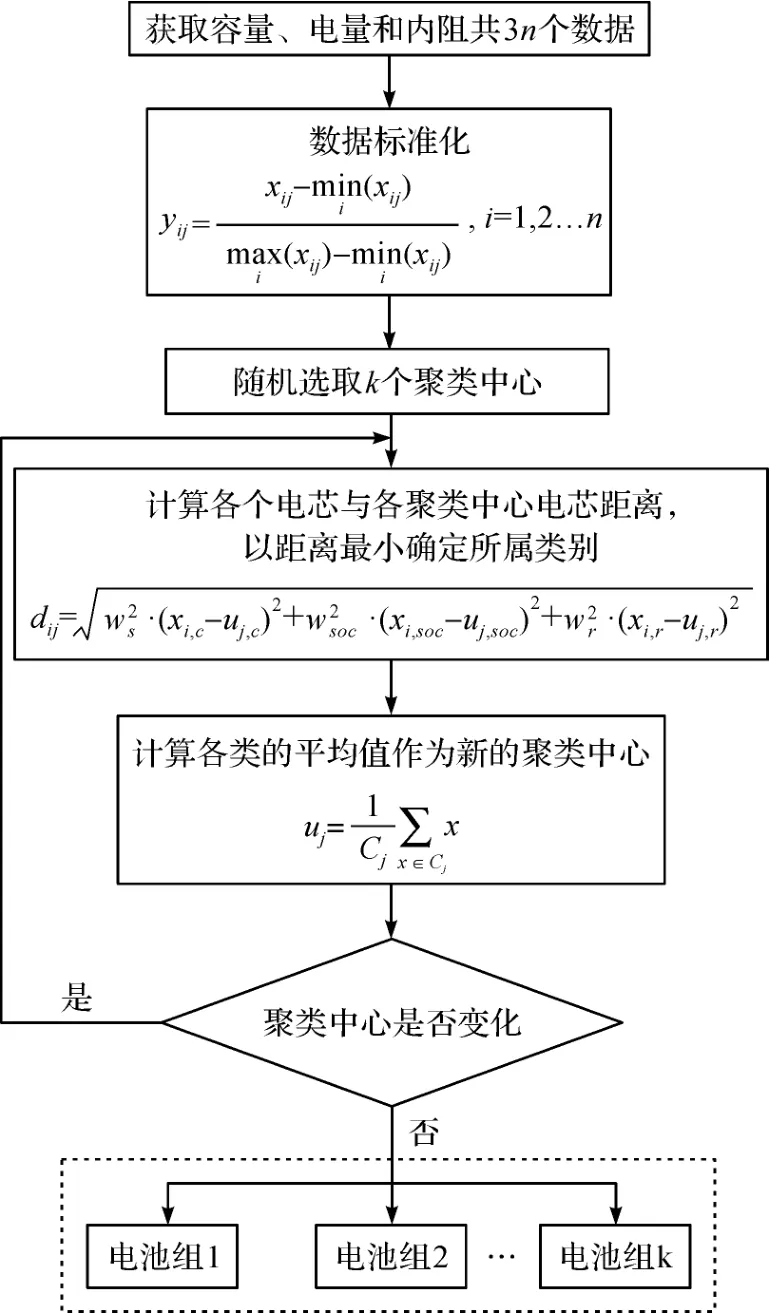
图1 退役电池聚类算法流程图

1.2 基于信息熵理论的权重设置

自从香农引入了描述热力学系统混沌程度的“熵”的概念之后［10-12］，信息熵成为一种定量描述信息分布特征和离散特征的方法，被广泛应用于信息随机性和混乱性综合评价。 由此开发了熵权评估方法，用于通信系统、模式识别和导航系统等领域对多对象、多评价因素系统的信息复杂度进行科学评估。 在信息论的研究中，信息量通常定义如下：

式中：p为信息的发生概率。 p越大，信息出现的概率越大，说明信息的不确定性。 数学期望定义为信息熵，假设给定信息源由离散随机变量X=｛x1，x2，…，xn｝，信息源X的熵可以表示为：

H（X）是表征信息源综合特征的量，其基本单位由对数底决定，本文中以自然数底e作为对数底，单位为Nat（奈特）。

在建立电池组的状态特征矩阵以及对特征矩阵归一化后得到了所有评价因子的归一化矩阵式Y后。 即可以利用熵权法确定每个评价因子的权重，具体计算步骤如下：

各评价因子的熵Sj如下：

其中k是与使样本的相关的常数。 值得注意的是当yij=0 时，ln（yij） =0。 Sj的值越大，数据的混乱程度越大，数据中包含的信息量也越大。

计算第j个评价因子的熵权，确定其权重并且所有wj之和等于1。 wj越小，权重越小，评价因子越不重要。

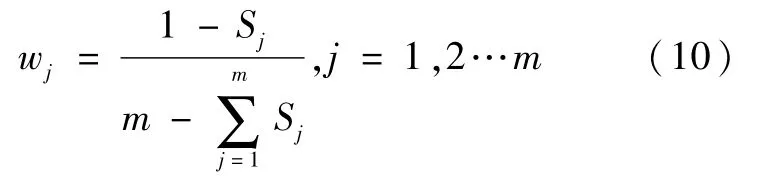
2 实验设计

为了验证本方法在退役电池组筛选重组上的有效性，我们对两辆同三元材料体系、不同行驶里程的实际运营电动车辆进行了充放电测试。 这两辆电动汽车分别为老化严重的锂离子电池组（命名为PackA）和轻度老化的电池组（命名为PackB），充电截止电压设置为厂家推荐的4.15 V，放电截止电压设置为厂家推荐的3.1 V。 PackA由96 个单体串联组成，并内置有18 个温度传感器。 实验中的电流、单体电压、温度等实验数据通过数据采集仪获得，并最终保存在电脑中。 单体电压采集精度约1 mV，电流采集精度约为0.1 mA，温度采集精度约0.1 ℃，实验的采样频率为1 Hz。 实验在25 ℃的温箱中进行。 实验的具体步骤如下：

（1）将电池组在25 ℃的温箱中静置3 小时，使电池系统达到热稳定；

（2）将电池组以1/3C恒流放电至放电截止电压；

（3）将电池组搁置30 分钟；

（4）将电池组以1/3C恒流充电2 小时；

（5）将电流切换至1/4C，继续恒流充电至充电截止电压；

（6）将电池组搁置30 分钟；

（7）将步骤（2）至步骤（6）循环5 次。

图2 描述了从实验中获取的时间、电流和电压等数据。 图2（a）（c）（e）描述了五次充放电循环过程中流过PackA的总电流、96 个单体的电压和PackA的总SOC；图2 紫色虚线框内的（b）（d）（f）展示了五次充放电循环过程中最后一次的充电数据。

图2 实验中的电流、单体电压和SOC

3 结果分析与讨论

3.1 聚类结果分析

基于实验室采集的电流、电压数据，可以计算得到电池组内各单体的容量、电量、内阻值。 进一步对容量、电量和内阻进行统计描述，结果如图3所示。 图3 显示了在PackA和PackB中电池各项指标分布都比较离散，而Pack B相对于PackA内阻和容量分布比较集中。 这些统计结果均表明电池组在使用一段时间后表现出较大的单体状态差异性，而这种现象将导致电池组使用寿命的下降与安全风险的提高。

图3 Pack A和Pack B容量、电量和内阻计算和统计结果

基于改进型k-means聚类算法分别对两个电池组进行聚类重组，电池组Pack A由96 个电池单体串联组成，且本次聚类设置6 个类别，具体的聚类结果如图4 所示，其中C1 -C6 代表聚类后不同类别的电池单体。 在三维空间中可看出Pack A聚类效果良好，各项性能指标相近的电池单体被分类到同一类别内。 为了能够详细地观察Pack A电池组聚类效果以及分析退役电池组可能的应用场景，将三维空间结果投影至二维上，如图4（b）（c）（d）所示分别为内阻-电量，内阻-容量以及容量-电量维度上的聚类结果。 观察图4（b）（c）（d）可以发现，C3 类别为异常单体，在本次聚类过程被识别出来。 经过筛选重组后的C1、C5类别在各个维度上分类效果都比较好，此时同一类电池的容量、电量和内阻的一致性均相对较高，因此分类后的电池适用于对模组能量储存能力和功率输出能力均要求较高的应用场景，同时这些重组后模组只需要经过小电流短时均衡后即具有较高的能量利用率。 而经过筛选重组后的C2、C4、C6 类别在容量、电量维度上一致性较高，在内阻维度上较为分散，因此这些经过重组后的电池适用于对能量密度要求较高的应用场景，同样只需要小电流短时均衡后即具备较高的能量利用率。

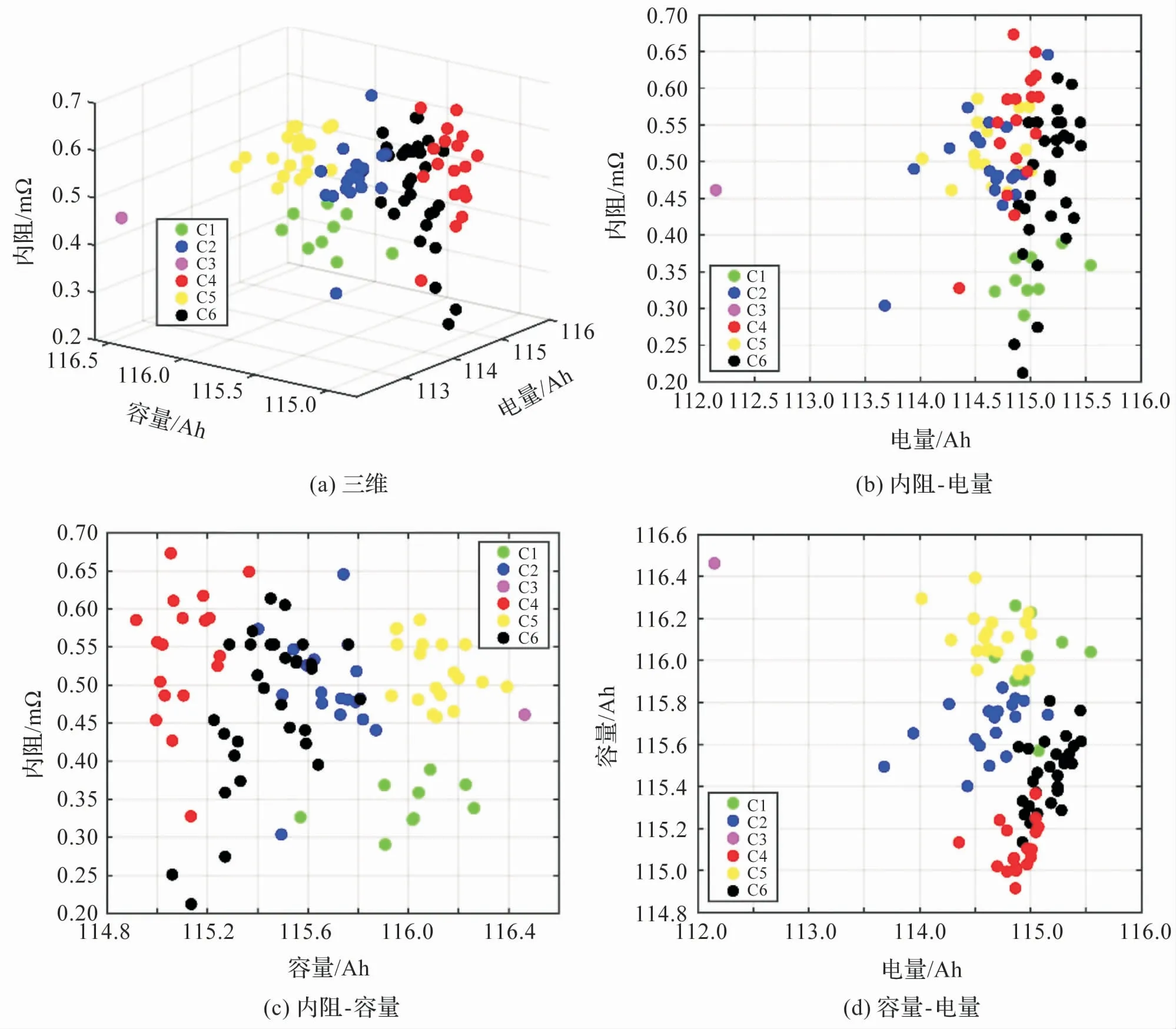
图4 PackA不同维度聚类结果

电池组PackB由88 个单体串联组成，聚类设置6 个类别，聚类结果如图5 所示。 以同样的方式分析Pack B电池组聚类结果及可能的应用场景，在三维图上可以看出分类效果良好，在二维图上可以看出类别C1、C2、C3、C4、C6 在容量-电量维度上分类效果较好，即分类后容量、电量一致性较高，同时这些重组后的模组均在内阻维度上表现出很高的一致性，因此分类后的C1、C2、C3、C4、C6 模组适用于对容量、电量和内阻均要求较高的能量型-功率型应用场景。 而分类后C5 类别只在内阻维度上表现出较高的一致性，而在容量、电量维度上的一致性较差，因此分类后的C5模组适用于对内阻要求较高的功率型应用场景。

图5 PackB不同维度聚类结果

3.2 聚类效果评价

上述只是对退役电池组聚类后效果的定性分析，并未检验筛选重组后退役动力电池组的一致性。 为了定量评价重组后退役动力电池的一致性，提出一种基于变异系数的一致性评价指标，对聚类后的电池充电电压曲线进行整体的一致性评价。 变异系数是概率论与统计学中衡量数据分布离散程度的一个归一化量度，其定义为标准差与平均值之比。 即当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，此时就应当消除测量尺度和量纲的影响，而变异系数可以做到这一点，它是原始数据标准差与原始数据平均数的比［13］。 本文中通过计算重组前与重组后电池组充电电压曲线变异系数评价一致性，具体计算公式如下：

式中：Vi-t表示第i个单体（共有n 个单体） 在充电阶段第t时刻（共有T个时刻）的电压；Vm-t表示在充电阶段第t时刻的各单体电压平均值，其全部数值构成充电过程的平均电压曲线；表示平均电压曲线的平均值；Vmax-t表示各电池单体在充电阶段第t时刻的最大电压值，其全部数值构成充电过程的最高电压曲线；Vmin-t表示各电池单体在充电阶段第t时刻的最小电压值，其全部数值构成充电过程的最低电压曲线；σV表示在充电阶段的最高电压曲线数据与最低电压曲线数据的均方根误差；δV表示各单体充电电压的变异系数，即评价电压一致性的参数。变异系数值越大，电池组电压一致性越差。

根据上述计算公式，可以获得如图6 所示PackA和PackB原电池组与筛选重组后C1 -C6模组的电压变异系数。 可以看出经过聚类后的退役电池模组的整体一致性均有显著提高。

图6 Pack A、PackB重组前与重组后电压变异系数

4 结 论

考虑退役电池组还具有较高的剩余使用价值，这些电池经过有效分选和重组后还可以应用于其他场景。 本文以动力电池容量、电量、内阻为评价指标，提出一种基于改进型k-means算法的退役电池组筛选重组方法，并根据聚类结果提出了重组后模组可能的应用场景。 进一步采用电压变异系数定量分析了重组后模组的一致性，结果表明经过聚类重组后的模组整体一致性有较大的提高。 该研究内容可为退役动力电池组重组方法以及重组后模组实际应用场景适应性提供新思路，从而完善动力电池组全生命周期价值链。