储能装置在多能流系统中的作用分析

秦宇翔，张卫军，周 乐

（1.辽宁科技大学 材料与冶金学院，辽宁 鞍山114000；2.东北大学 工业炉研究所，辽宁 沈阳110000）

0 引 言

为了解决目前存在的环境与能源的双重压力，多能流系统受到了广泛关注［1，2］。

多能流系统可以同时提供冷量、热量、电量，具有较高的能源利用率［3，4］与较高的运行可靠性［5］。 可再生能源具有清洁、环保、廉价的特点，将二者耦合可以使系统更为高效、清洁。

但是，太阳能、风能等可再生能源容易受自然环境因素的影响，导致光伏与风力发电机的出力具有随机性、波动性、不确定性［6］。 冷、热、电等负荷的需求量也随着环境、季节、用户用能习惯的变化而变化，也具有不确定性［7］。 源荷不确定性对系统运行计划的制定，以及稳定运行带来了极大的挑战［8］。 随着多能流系统的日益推广，源荷不确定性问题必须加以重视［9］。

目前，对于多能流系统进行了大量研究，文献［10］以对环境影响最小为目标，提出了光伏/光热与天然气互补的冷热电多联供系统的鲁棒多目标优化模型，并采用NSGA II算法求解，采用实例论证了算法的有效性。 甘霖等［11］建立了微网的优化调度模型，并与冷热电独立微网进行对比，结果表明多能流微网系统可以降低运行费用，提高可再生能源消纳率，但并未考虑源荷不确定性对系统的影响。 熊文等［12］考虑了微网多能流系统中储热、蓄冷装置的盈利策略，据此研究了储热、储冷装置在不同供能季的最优容量配置与运行策略。 汤翔鹰等［13］采用多时间尺度优化调度来平抑波动，在日前调度过程中考虑了多能灵活性，使系统在日内调度中可以协调各设备应对负荷功率的波动。 姜慧楠［14］建立了系统运行费用最小的目标函数，采用多时间尺度优化的方法来逐次降低可再生能源与负荷的预测误差对系统调度的影响，结果表明多时间尺度调度可以增加系统跟踪负荷的能力。 李佳慧［15］在灰色神经网络组合法对系统典型日光伏电池、风机的输出功率进行预测的基础上，进行了系统的多目标优化运行研究。但是，一般认为，根据预测数据计算误差较大［16］。文献［17］采用蒙特卡洛法分析了不确定性对CCHP系统的能源和经济性能的影响。 但以上文献并未探讨调度结果的安全裕度，以及系统配置储能装置的必要性。

基于以上问题，本文将设计两种多能流系统，其中一种配备储能装置（下文简称有储能系统），一种没有配备储能装置（下文简称无储能系统），然后对比两系统在运行费用、能源效率、安全裕度、运行费用受负荷不确定性影响大小等方面的差异，从而探讨储能装置的作用。

1 有储能系统模型

多能流系统由输入能源、能源转换设备、负荷组成［18，19］。 本文输入能源有风能、太阳能、天然气、电网购电。 燃气轮机、电制冷机、吸收式制冷机、换热器、电锅炉作为能源转换设备，生产系统所需电量、冷量和热量。 系统配备储热、蓄冷设备，蓄电池。 系统如图1 所示。

图1 配备有储能装置的多能流系统示意图

1.1 设备数学模型

1.1.1 燃气轮机

燃气轮机输入天然气，产生电能及热能。 其能量输入—输出数学模型及约束为：式中：PGT，t表示t时刻燃气轮机的输出功率；Pgas，t为t时刻天然气燃烧产热量；ηGT为燃气轮机的效率；分别为燃气轮机输出功率的最小、最大值；QGT，t为燃气轮机的产热量；θHE为燃气轮机的热电比。

1.1.2 余热锅炉

余热锅炉是将燃气轮机的余热回收加以利用的装置。 其数学模型为：

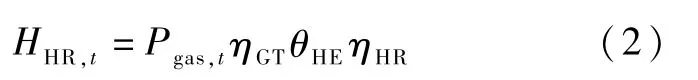
式中：ηHR为余热锅炉的效率；HHR，t为余热锅炉t时刻输出的热量。

1.1.3 吸收式制冷机

吸收式制冷机利用余热锅炉的热量进行制冷，其数学模型及约束条件为：

式中：HAR，t为t时刻吸收式制冷机的输入功率；ηAR为吸收式制冷机的制冷系数；KAR，t为t时刻吸收式制冷机输出功率；分别为机组输出的最小、最大功率。

1.1.4 换热器

换热器利用余热锅炉的余热作为输入能源，产生热量。 其数学模型与约束为：

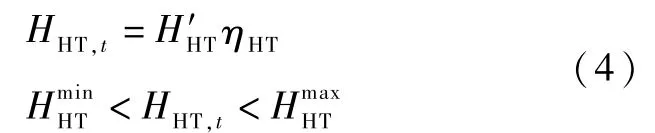
式中：H＇HT为t时刻输入到换热器的热量；ηHT为换热器的效率；HHT，t为t时刻换热器输出功率；分别为换热器输出热量的最小、最大值。

1.1.5 蒸汽轮机

蒸汽轮机利用余热锅炉输出的热量发电，其数学模型与约束为：

式中：PST，t为t时 刻 蒸 汽 轮 机 输 出 功 率；HST，t为 余热锅炉输入蒸汽轮机的热量；ηST为蒸汽轮机发电效率；分别为蒸汽轮机输出功率上下限。

1.1.6 电制冷机

电制冷机将电能转换为冷能。 其数学模型与约束条件为：

式中：PEC，t为t时刻电制冷机的输入功率；ηEC为制冷机的电冷转换效率；KEC，t为t时刻电制冷机的输出功率；分别为电制冷机输入功率的最小、最大值。

1.1.7 电锅炉

电锅炉将电能转换为热能。 其数学模型与约束条件为：

式中：PEH，t为t时刻电锅炉的输入功率；ηEH为电锅炉效率；HEH，t为t时刻电锅炉的输出功率；分 别为电锅炉输入功率的最小、最大值。

1.1.8 储热装置

储能装置是跨时间段利用能量的装置，其在平谷电价时段存储能量，在高电价时段释放，可以对电网起到削峰填谷的作用。

储热装置的数学模型及约束为：

1.1.9 蓄冷装置

蓄冷装置的数学模型及约束为：

1.1.10 蓄电池

蓄电池的数学模型及约束为：

1.2 系统数学模型

1.2.1 系统能量平衡

式（11） -（13）分别为冷量平衡、热量平衡、电量平衡表达式。 ωPV，t、ωWT，t分别表示t时刻系统对太阳能与风能的消纳率。 PWT，t、PPV，t分别表示t时刻风电与光伏实际的出力。 Pbuy，t表示t时刻购电量。

1.2.2 节点能量平衡

式（14） -（21）分别代表燃气轮机、余热锅炉、储热装置、蓄冷装置、蓄电池的输入输出关系。Q1、Q2分别代表燃气轮机余热，余热锅炉热损失。θHE为燃气轮机热电比，取1.2。

2 无储能系统模型

无储能系统不配备储能装置，其余结构与有储能系统完全相同。 系统如图2 所示。

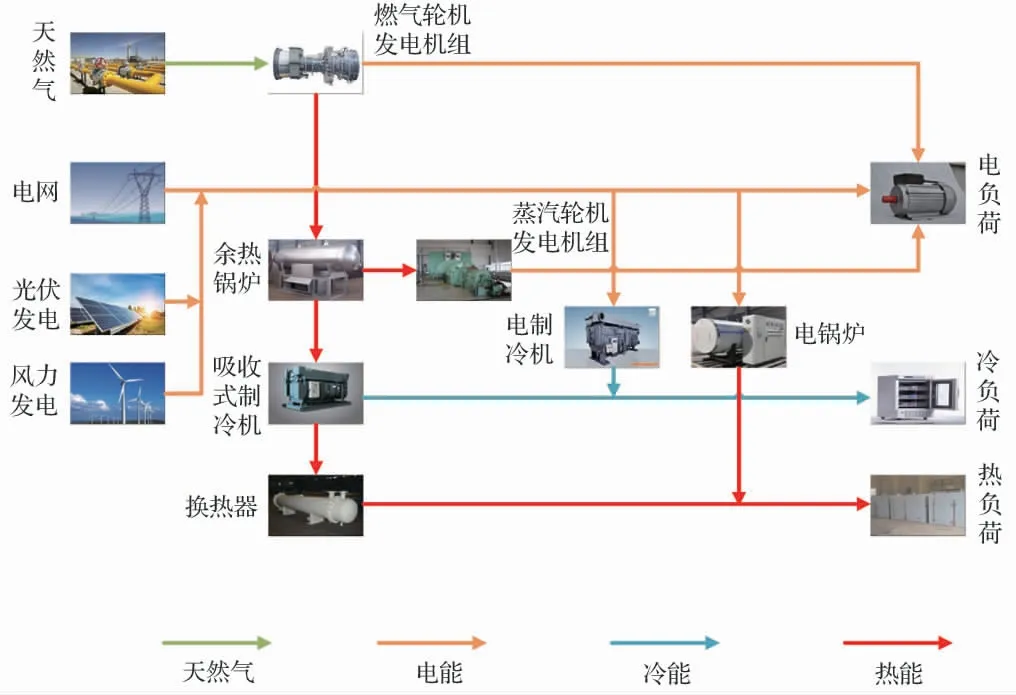
图2 无储能系统示意图

2.1 设备数学模型

同式（1） -（7）。

2.2 系统数学模型

2.2.1 系统能量平衡

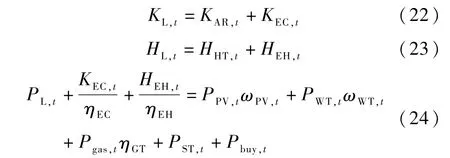
式（22） -（24）分别代表冷、热、电能平衡。

2.2.2 节点能量平衡

同式（14） -（15）。

3 系统优化调度

3.1 有储能系统优化模型

以夏季典型日24 h 总运行成本最小为目标函数，如下式所示：

式中：Cenergy，t表示t时刻的能源费用，包括购气，购电费用、光伏以及风力发电机的运行费用；Cdev，t表示能源转换设备运行费用，包括余热锅炉（HR）、换热器（HT）、吸收式制冷机（AR）、电制冷机（EC）、电锅炉（EH）、蒸汽轮机（ST）、燃气轮机（GT）的运行费用；Cstor，t表示储能设备运行费用；Caban，t表示弃风弃光惩罚费用；c表示各设备的单位运行费用；QLHV代表天热气低热值，取9.7 kWh/m3、分别代表单位弃光弃风成本，取为0.05元/kW；ce，t、cgas分别表示电价与天然气价格。

约束条件包括式（1） -（13），以及余热利用效率约束式（26）与余热锅炉输出热量的利用率约束式（27）。

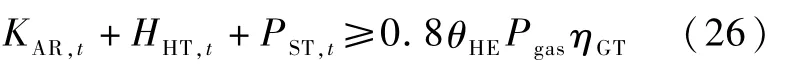
此模型是一个混合整数线性规划问题，通过matlab 软件进行求解。

3.2 无储能系统优化模型

约束条件如式（1） -（7）、（22） -（24），（26 -27）。

此问题是线性规划模型，采用matlab 平台求解。

4 源荷不确定性分析

4.1 风力发电机

风力发电的主要影响因素是轮毂处的风速［20］。 风速的随机波动导致风力发电机的出力具有随机性、波动性、不确定性。 目前，公认的描述风速的最佳分布为威布尔分布［21-23］。

风速威布尔分布的概率密度函数及概率分布函数如式（28）、式（29）所示：

式中：V为风速；K与C分别代表形状参数与尺度参数。

由风速得到风力机组的输出功率，如式（30）所示：

式中：V表示风速；Vin、Vout分别代表切入风速、切出风速；Pnorm、Vnorm分别代表额定功率、额定风速；

4.2 光伏电池

光伏的输出功率与光照强度、环境温度等因素相关。 大量研究表明，太阳光照强度近似服从贝塔分布［24，25］。 具体如式（31）所示：

式中：Γ为伽马函数；α、β 分别为尺度参数与形状参数。

研究表明，随着温度的上升，太阳能电池的开路电压减小，光电流略微增加，所以光伏电池的输出功率随着温度的上升而减小［26］。

太阳电池的电流与光照强度基本成正比，而光照强度对电压影响很小［26］，所以，光伏电池的功率与光照强度近似成正比关系。 由光照强度可得光伏输出模型，如式（32）所示

4.3 负 荷

负荷主要受环境、气候、用户用能习惯影响［7］。 研究表明，负荷服从正态分布［27，28］，其概率密度函数如式（33）所示：

式中：∂为负荷值；μ与σ2分别为负荷的均值与方差。

5 算例分析

本课题以某工业园区为研究对象，系统所用设备的参数及电费结构如表1 -表3 所示，天然气费用按5 元/m3计算。

表1 设备参数

表3 电价表

以园区所在地夏季典型日光伏、风力发电机的出力，以及冷热电负荷数据为基础，计算典型日各设备的运行计划，使系统典型日运行费用最少。 可再生能源出力、冷热电负荷分别如图3、图4 所示。

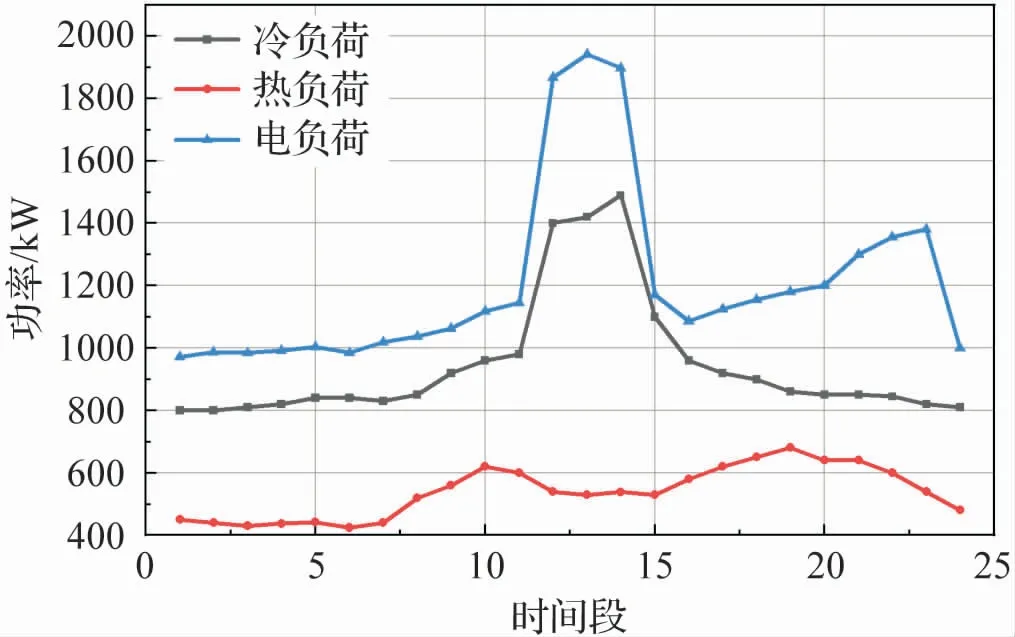
图3 风电、光伏出力数据

图4 冷、热、电负荷数据

表2 储能设备参数

5.1 调度结果分析

根据调度模型，得出两系统的优化结果（见图5 至图7）。

图5 表明了两系统所需的冷能在1 -11 点、15 -19 点，以及24 点时都完全由电制冷机供给。12 -14 点、20 -23 点，系统不再向电网购电，有储能系统所需冷量由电制冷机、吸收式制冷机、蓄冷装置共同供给。 而对于无储能系统，冷量只能由电制冷机与吸收式制冷机提供，所以，此时的吸收式制冷功率与电制冷功率明显大于有储能系统。

图5 两系统冷量优化结果

蓄冷装置在低电价时段的1 -7 点存储冷量，在高电价时段的12 -14 点、20 -23 点释放出来，减轻了吸收式制冷和电制冷机的供能负担，起到了削峰填谷的作用。

图6（a）表明了有储能系统所需的热能在1-11 点、15 -16 点，以及24 点时完全由电锅炉供给。 12 -14 点、20 -23 点的高电价时段，热量由电锅炉、换热器、储热装置共同供给。

储热装置在低电价的1 -11 点以及16 点存储热能，在12 -14 点、17 -23 点释放，减轻了换热器和电锅炉的供能负担，起到了削峰填谷的作用。

图6（b）表明了无储能系统所需的热能在低电价时段1 -11 点、15 -19 点，以及24 点时完全由电锅炉供给。 电价峰值时段的12 -14 点、20 -23 点，换热器与电锅炉共同提供热量，且此时二者的供能负担大于有储能系统。

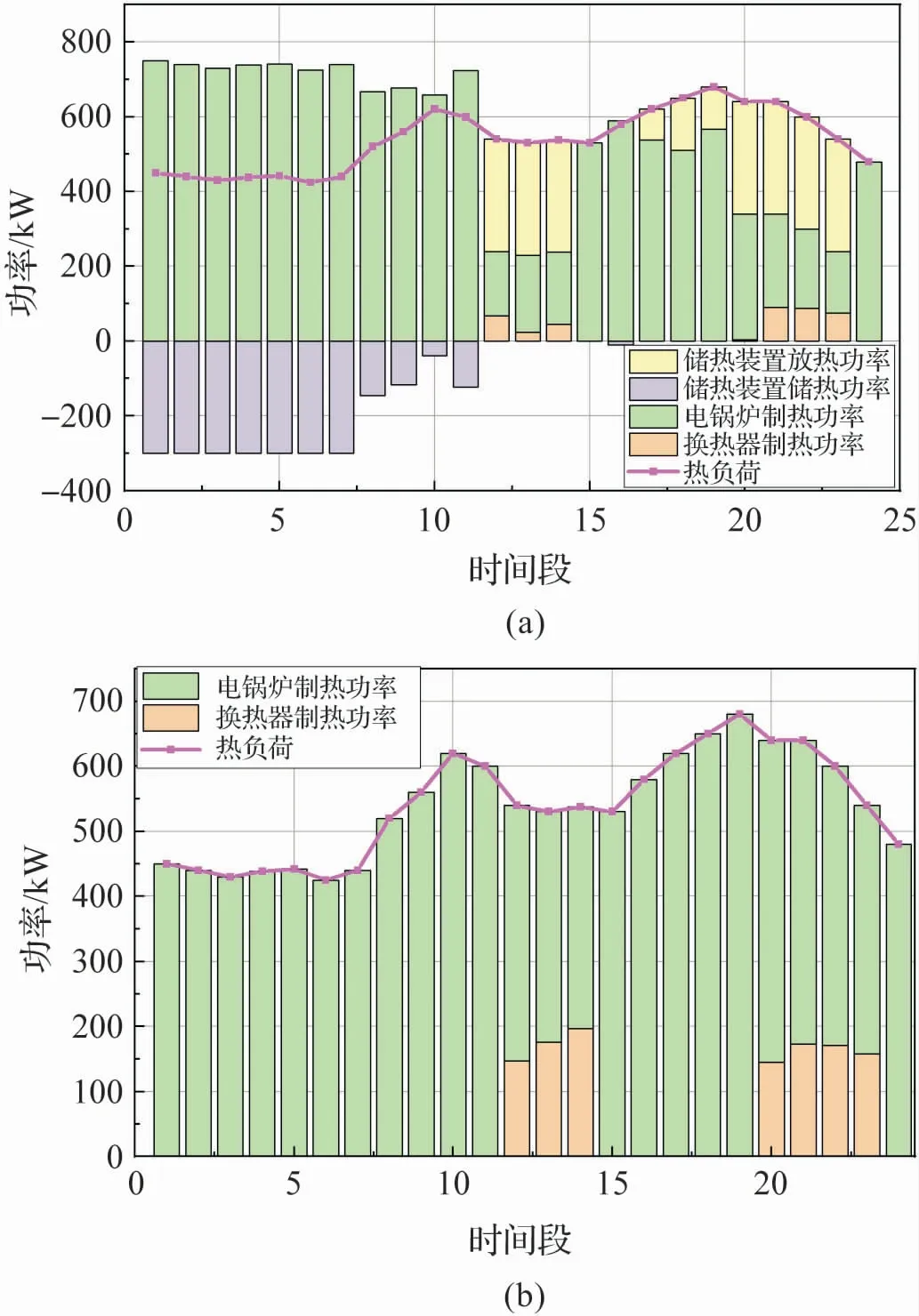
图6 热量优化结果

图7 表明了两系统所需的电能在1 -11 点、15 -19 点，以及24 点时均由可再生能源和电网购电供给。 在12 -14 点、20 -23 点，有储能系统所需电能由燃气轮机、可再生能源、蓄电池共同供给。 而无储能系统电负荷仅由燃气轮机与可再生能源供给，供能灵活性不足，不具有削峰填谷的能力。

图7 电量优化结果

蓄电池在低电价的1 -7 点存储电量，在高电价的13 -14 点、20 点释放电量，起到了削峰填谷的作用。

从以上分析可知，储能装置在电价平谷时段存储能量，电价峰值时段利用能量，即减少了系统的运行费用，也起到了削峰填谷的作用。 从优化结果可以得出储热装置、蓄冷装置、蓄电池的最佳容量分别为2500 kWh、2060 kWh、1350 kWh。

5.2 运行费用分析

两系统运行费用不相同，但变化趋势基本相同。 由于不同时刻供能方式不同，各时刻的运行费用相差较大。 图8 表明，运行费用与分时电价有一定关联。 对于无储能系统，12 -14 点以及20-23 点系统运行费用较高，电价平谷时段运行费用较低。 这是由于在峰值电价时段，系统购买天然气，启动燃气轮机、换热器、吸收式制冷机，而其他时段工作设备较少，所以，电价峰时段运行费用较其他时段高。

图8 运行费用对比

有储能系统在电价低谷时期，购买大量电能进行存储，该时段运行费用较高，而在电价峰值时段储能装置释放能量，使系统购气量较少，所以该时段运行费用低于无储能系统，也导致了有储能系统典型日运行费用较低。 计算可得，配备储能装置可使系统典型日的运行费用降低25%。

5.3 能源利用效率分析

图9 表明典型日两系统的能效变化趋势大体相当，都具有平电价时段较大、峰谷时段较小的特性。 这是由于系统在电价峰值时段会增加购气量，在电价谷时段会增加购电量，所以系统整体能效下降。 除电价谷时段外，有储能系统的能效较无储能系统高，这与有储能系统在电价谷时段消耗较多一次能源，而在其他时段消耗较少一次能源有关。 有储能系统与无储能系统的能源利用效率计算分别如式（34）、（35）所示。

图9 能源利用效率对比

式中：ηt为系统能源利用效率；Kt、Ht、Pt分别表示t时刻冷量、热量、电量的需求量；ηge、ηtran分别表示电厂发电效率与电网传输效率。

5.4 调度结果裕度分析

本节基于安全供能原则，研究系统各时刻的优化结果所具备的裕度，即各时刻系统允许的负荷及可再生能源出力的最大波动率。 其中，可再生能源的波动率如式（36）所示，负荷波动率如式（37）所示。

5.4.1 光伏波动下限

以任意时刻光伏出力最小值为目标函数，与同时刻光伏出力进行比较，得出波动率。 计算结果如图10 所示。

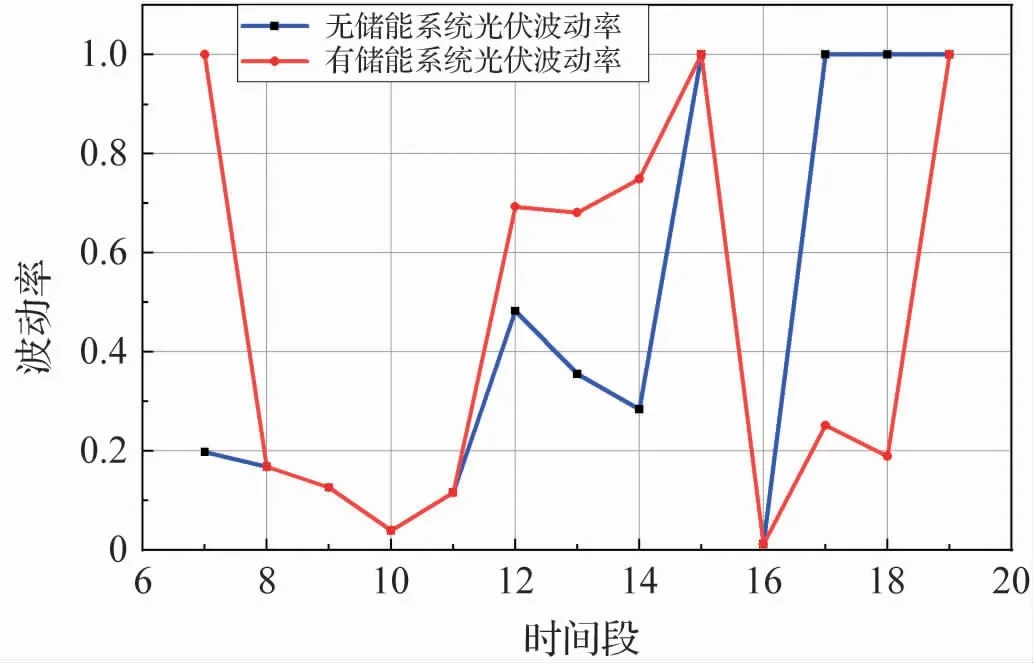
图10 光伏波动率

有储能系统：

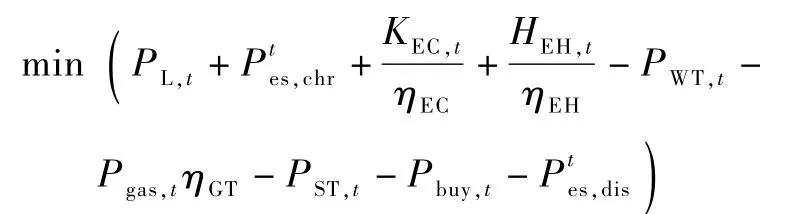
约束条件：

无储能系统：

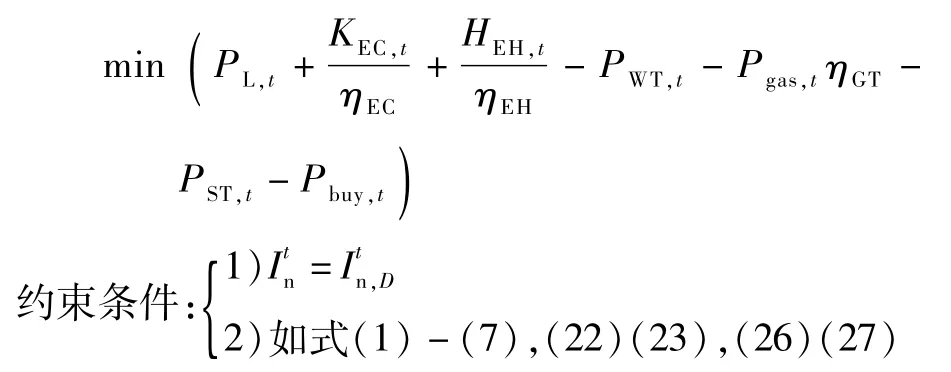
5.4.2 风力发电机波动下限

以任意时刻风机出力最小值为目标函数。

有储能系统：

约束条件：

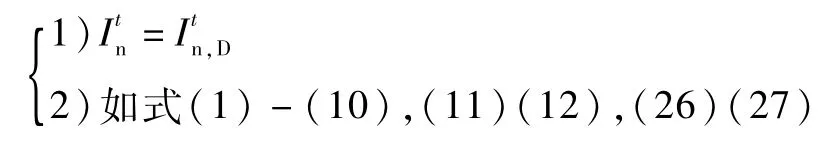
无储能系统：

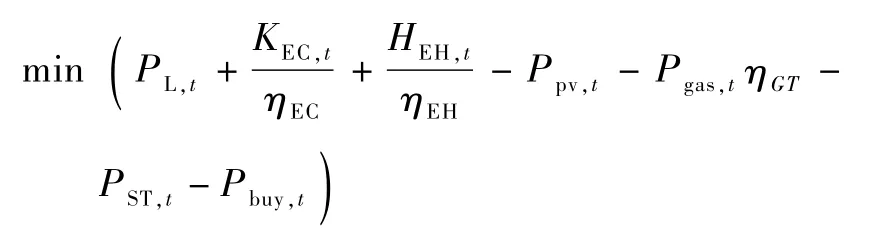
约束条件：

图10、图11 表明，在大部分时间段，有储能系统比无储能系统能为可再生能源出力提供更大的下降空间。 具体原因如下：

图11 风机组波动率

7 点：无储能系统仅仅通过提高光伏消纳率来为可再生能源出力提供下降空间，而有储能系统可以通过增加购电量、使储能装置停止储能两个途径来提供更大的下降空间。

12 -14 点、20 -23 点：两系统都通过增加购气量为可再生能源出力的下降提供空间。 但无储能系统在该时刻的购气量较大，受燃气轮机出力限制，所增加的量有限，为可再生能源出力提供的下降空间小于有储能系统。 有储能系统在12 点通过释放冷量也为可再生能源的出力提供了下降的空间。

19 点无储能系统只能通过增加购电量来为风力发电机的出力提供下降空间，而有储能系统可以通过增加购电量，增加储热装置放热量为风力发电机出力的下降提供空间，可以提供的空间大于无储能系统。

17 -18 点无储能系统允许可再生能源的出力的下降范围反而较大。 主要由于无储能系统可以通过增加购电量来弥补可再生能源出力的下降，而有储能系统受调度计划约束，无购电计划，所提供的可再生能源下降范围较小。

5.4.3 冷负荷波动上限

以任意时刻冷负荷最大值为目标函数。

有储能系统：

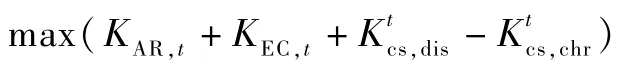
约束条件：

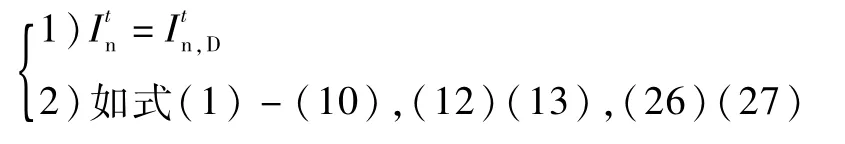
无储能系统：

约束条件：

图12 表明，在大部分时间段，有储能系统允许冷负荷增加量大于无储能系统。 具体原因如下：

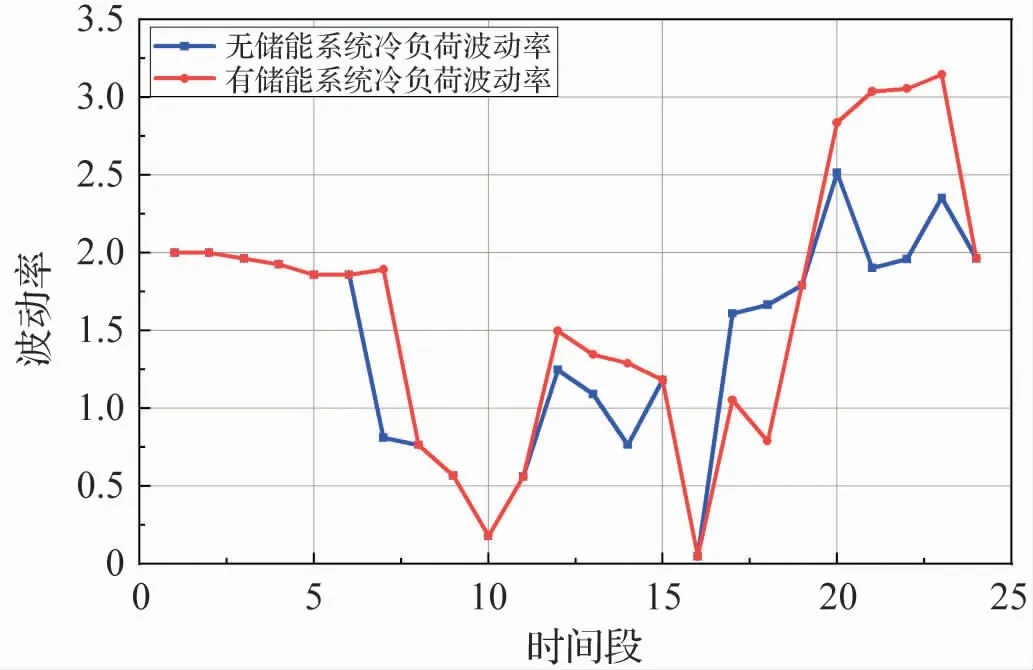
图12 冷负荷波动率

7 点：无储能系统只能通过提高光伏消纳率来应对冷负荷的增加，可提供的空间有限。 而有储能系统可以通过停止储能装置储能来增加电制冷量，可以为冷负荷提供更大的上升空间。

12 -14 点，20 -23 点：两个系统都通过增加购气量来提高电制冷量与吸收式制冷量，但无储能系统受燃气轮机功率限制，只增加较小的购气量。 另外，有储能系统在12 点增加蓄冷装置放冷量，也为冷负荷提供上升空间。

17 -18 点，无储能系统可以通过增加购电量来提供更多的电制冷量，而有储能系统受调度计划约束，在该时段无购电计划，只能通过增加储热装置放热量为冷负荷提供上升空间，所以，此时无储能系统所能提供的负荷上升空间反而较大。

5.4.4 热负荷波动上限

以任意时刻热负荷最大值为目标函数。有储能系统：

约束条件：

无储能系统：

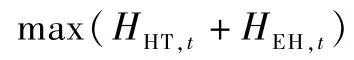
约束条件：

图13 表明，在所有时间段，有储能系统比无储能系统能提供更大的热负荷上升空间。 具体原因如下：

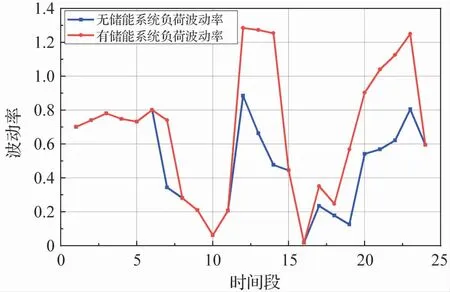
图13 热负荷波动率

7 点：无储能系统通过提高光伏消纳率来增加电锅炉产热量。 而有储能系统可以通过停止储能装置储能来增加电锅炉产热量，可以提供更多的热负荷上升空间。

12 -14 点、20 -23 点：两系统都是通过增加购气量来提供热负荷上升空间，该方法可以提高换热器以及电锅炉的产热量。 但有储能系统的购气量更多，并且蓄冷装置在12 点释放冷量，所以可以提供更大的负荷上升空间。

17 -19 点无储能系统通过增加购电量来提高电锅炉的产热量，而有储能系统通过增加储热装置的放热量以及购电量来提高热负荷的波动上限。

5.4.5 电负荷波动上限

以任意时刻电负荷最大值为目标函数。有储能系统：

约束条件：

无储能系统：

约束条件：

图14 表明，在大部分时间段，有储能系统可以比无储能系统提供更大的电负荷上升空间。 具体原因如下：

图14 电负荷波动率

7 点：无储能系统只能通过提高光伏消纳率来为电负荷的增加提供空间，而有储能系统通过增加购电量，停止储能装置储能来提供比无储能系统更大的电负荷增量范围。

12 -14 点、20 -23 点：无储能系统通过增加购气量来提高可供电量，但受调度计划限制，可以增加的购气量少于有储能系统。 另外，有储能系统还在12 点通过增加蓄冷装置放能，提供更大的电负荷增量范围。

17 -18 点，无储能系统可以通过增加购电量来提供更大的电负荷增量空间，而有储能系统受调度计划限制，无购电计划，虽然可以增加储热装置放热量，但所能提供的电负荷上升空间小于无储能系统；19 点无储能系统只能增加购电量，而有储能系统既增加购电量、又增加储热装置放热量，故有储能系统可以提供更大的电负荷上升空间。

5.5 光伏消纳率

可再生能源消纳率是衡量系统可再生能源利用水平的重要指标。

图15 表明了无储能系统在7 -11 点、16 点存在弃光现象，经过计算，共弃光654 k Wh，而有储能系统由于储能装置可以存储多余的可再生能源，不存在弃风弃光现象，可再生能源消纳率100%。 这也就证明了储能装置可以提高可再生能源消纳率。

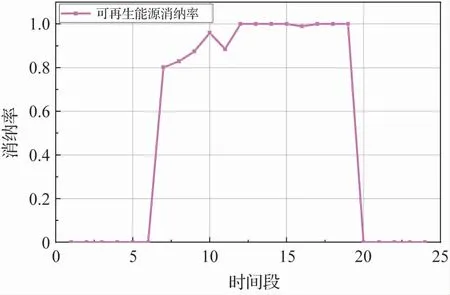
图15 无储能系统光伏消纳率

5.6 负荷不确定性分析

采用蒙特卡洛法来研究负荷不确定性对系统运行费用的影响，蒙特卡洛法是用计算机模拟的方法产生随机抽样结果，根据抽样产生的随机数来计算所求问题的方法。

文献［18］表明，系统各时刻的冷、热、电负荷都满足正态分布，且正态分布的标准差σ与均值的关系满足σ=0.1，根据这一关系可以得出冷、热、电负荷各时刻服从的正态分布的概率密度函数，从而抽样1000 次得到每一时刻的1000 个负荷值，用这些随机数去计算典型日一天的最小运行费用变化情况。 从而得出不确定性对运行费用的影响范围，结果采用箱线图表示。

5.6.1 冷负荷不确定性对运行费用的影响

图16（a）表明了对于有储能系统，即使某些时刻存在冷负荷突变的情况，但是储能装置会通过储放能量来平抑波动，使得负荷的波动对其他设备的影响较小，所以，对于有储能系统，任一时刻冷负荷的波动对一天运行费用的影响都在一定的范围之内，不会出现太多异常值。 另外，由于储能装置削峰填谷，能量可以跨时间段利用，这使得系统一天的运行费用低于无储能系统。

图16（b）表明，对于无储能系统，10 点、16 点存在大量异常值，这主要是由于在这些时刻冷负荷波动较大，因而产生了较多异常值。

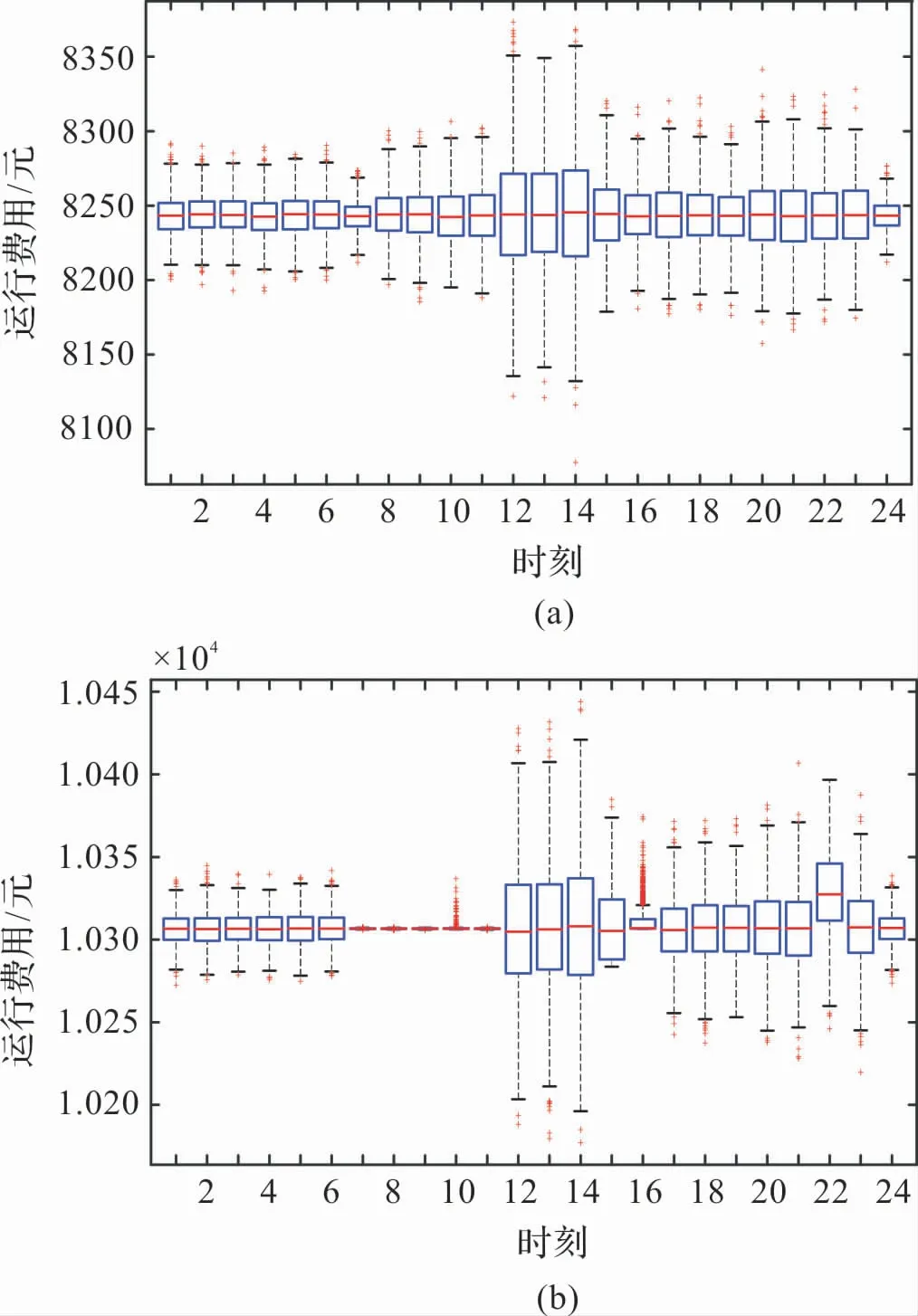
图16 冷负荷不确定性对运行费用的影响

5.6.2 热负荷不确定性对运行费用的影响

图17（a）表明，热负荷波动对有储能系统的运行费用影响较为平缓。 图17（b）表明，无储能系统在9 -10 点、16 点、19 点存在大量异常值，这主要是由于在这些时刻热负荷波动较大。

图17 热负荷不确定性对运行费用的影响

5.6.3 电负荷不确定性对运行费用的影响

图18（a）表明了电负荷波动对有储能系统的运行费用影响较为平缓。

图18（b）表明，无储能系统在7 -11 点、15、16 点存在大量异常值，这是由于在这些时刻电负荷波动较大，导致系统购电量以及运行费用波动较大，产生较多异常值，导致一天的费用变化幅度较大。

图18 电负荷不确定性对运行费用的影响

通过以上分析可以得出，储能装置的存在，可以平抑各种负荷的波动，进而使得系统的运行调度方案随着负荷的波动变动较小，进而导致运行费用波动也较小。

6 结 论

本文通过优化调度得出储热装置、蓄冷装置、蓄电池的最佳容量分别为2500 kWh、2060 kWh、1350 k Wh。 通过两系统对比得出储能装置的如下作用：

（1）不考虑设备初始投资，可以降低系统25%的运行费用。

（2）当蓄电池容量与可再生能源装机容量近似为1 ∶4 时可使可再生能源消纳率达到100%。

（3）在大部分时刻允许源荷两侧的波动范围更大。

（4）系统典型日最小运行费用受负荷不确定性影响较小。

但是在典型日调度结果安全裕度方面，有些时间段有储能系统裕度要小于无储能系统，说明在这些时段配备储能装置反而会减少系统裕度，但是大部分时段还是要优于无储能系统。 说明多能流系统配备储能装置是非常必要的。