辨析动能定理和动量定理
山东 李德林
动能定理和动量定理都是重要的物理学规律,有些问题看似用动能定理和动量定理都能解决,实则不然,本文选取几种学生容易出错的物理情境并加以分析,透过表象看本质,加深学生对动能定理和动量定理的理解程度,提高学生精准选取动量定理或动能定理分析实际问题的能力,提升学生的核心素养。
1 两定理在变力作用下的非匀变速运动中的应用
【例1】如图所示,MN、PQ是两条水平放置彼此平行的金属导轨,匀强磁场的磁感线垂直导轨平面。导轨左端接阻值R=1.5 Ω的电阻,电阻两端并联一电压表,垂直导轨跨接一金属杆ab,ab的质量m=0.1 kg,电阻r=0.5 Ω。ab棒与导轨间的动摩擦因数μ=0.5,导轨电阻不计。现用F=0.7 N的水平力向右拉ab,使之从静止开始运动,经时间t=2 s后,ab开始做匀速运动,此时电压表示数U=0.3 V。重力加速度g=10 m/s2,求:
(1)ab棒匀速运动时,外力F的功率;
(2)ab棒加速运动的距离。

图1
【解析】(1)ab棒匀速运动时,电路中电流
由平衡条件可得F=BIL+μmg,代入数据可得
BL=1 T·m

所以当ab棒匀速运动时,外力的功率P=Fv=0.28 W
(2)解法1:用动量定理求解


联立解得,ab棒加速运动的距离s=0.72 m。
解法2:用动能定理求解

联立解得,ab棒的加速运动距离s=0.76 m
【点评】导体棒做变速运动,运动过程中受到的安培力是变力,且在动能定理和动量定理表达式中都用平均值表示,但是这两个平均力的物理意义却不相同。动量定理中的平均力是对时间的平均力,而动能定理中的平均力是对位移的平均力,学生出错的原因是对平均安培力的概念认识不到位,没有深刻理解两种平均力的本质,导致应用时不能区分清楚。

表1
2 两定理在连续体模型(软绳、链条等)中的应用
【例2】一匀质柔软细绳长度为L,质量为m0,堆放在光滑的水平地面上,某人手提细绳的一端,以速度v匀速竖直向上提起,求细绳全部被提起时拉力所做的功。
解法1:用动能定理解答
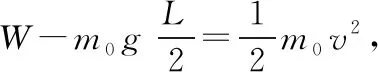
解法2:用动量定理解答


【点评】本题用动能定理和动量定理两种解法看似都合理,但只要仔细分析运动过程就会发现,在由静止变为向上运动的极短时间内,细绳的每一小段速度发生了突变,绳子的内力做了功,这个过程中有机械能的损失,可等效为完全非弹性碰撞模型,因此解法1把整个细绳整体作为研究对象,用动能定理列方程求解是错误的,而解法2用动量定理解答才是正确的。如果将题目的运动过程改成缓慢的拉起细绳,就不会存在速度突变,也就没有机械能的损失,则用动能定理求解就没有问题了。对软绳、链条等连续体模型,运动过程各部分速度不同,过程中通常要注意机械能的损失,对于此类问题可以取一微小时间段建立微元模型,再用动量定理分析,进而获得突破。
3 两定理在物体与流体相互作用中的应用
【例3】航天器在远离星球的宇宙空间飞行时,其他星球对航天器的万有引力可以忽略不计,航天器不受外力作用将做匀速直线运动。假设有一航天器,正以速度v在宇宙中航行,航天器可以简化为横截面积为A的圆柱体。某时刻航天器将进入一大片处于静止状态的微陨石云层,微陨石云质量分布均匀,密度为ρ,假设微陨石碰到航天器时,立即被吸附到航天器表面。为了使航天器能以原来的速度v匀速航行,需要启动航天器发动机,求航天器需要增加的功率应为多大?
解法1:用动能定理解答

解法2:用动量定理解答
取一微小时间段Δt,在航天器前方长度为vΔt,横截面积为A圆柱体内的微陨石质量为m=ρAvΔt。在时间Δt内,航天器与质量为m微陨石碰撞,设航天器对陨石碰撞时的作用力为F,对质量为m的微陨石,根据动量定理得FΔt=mv,解得F=ρAv2,则航天器受到微陨石云的阻力大小也为F,因此航天器若要保持原来的速度做匀速运动,则需增加的功率为P=Fv=ρAv3。
【点评】微陨石吸附到航天器上,属于完全非弹性碰撞模型,碰撞过程有机械能损失,解法1用动能定理求解时,只考虑了陨石增加的动能,却没有考虑航天器与陨石碰撞损失的机械能,因此解法1是错误的,解法2用动量定理解答才是正确的。


与解法2的分析结果完全相同,因此不管这一类问题是否有机械能损失,如果对能量的分析很全面,通过构建恰当的物理模型,也完全可以用能量观点解题。
分析动力学问题,有三大基本规律,即牛顿运动定律、能量观点和动量观点,能量观点和动量观点要比牛顿运动定律的应用范围广,有些复杂的运动形式和作用过程,并不适合用牛顿运动定律解决,此时通常要从能量观点和动量观点入手分析,而动能定理和动量定理又是其中的核心规律,所以在应用时要根据具体的物理情境挖掘关键信息和隐含条件,建立正确的物理模型,根据建立的模型特点决定选择使用动能定理还是动量定理,避免造成对两个定理的滥用或混用。

