带电粒子在环形磁场中运动的临界探讨

贵州 范钟润

带电粒子在有界磁场中运动的临界问题是物理高考的热点问题，该类问题的考查方式丰富，对学生的理解能力、推理能力、分析综合能力、应用数学知识解决物理问题能力都有较高要求，是教学中的一大难点，也是很多学生处理带电粒子在匀强磁场中运动的一大障碍。本文通过对2020年全国卷Ⅲ第18题和贵州省2022年适应性考试第18题以及2022年八省T8联考第10题分析对比，就环形磁场对带电粒子的约束问题做出探讨与归纳。

一、原题呈现

(2020·全国卷Ⅲ·18)真空中有一匀强磁场，磁场边界为两个半径分别为a和3a的同轴圆柱面，磁场的方向与圆柱轴线平行，其横截面如图1所示。一速率为v的电子从圆心沿半径方向进入磁场。已知电子质量为m，电荷量为e，忽略重力。为使该电子的运动被限制在图中实线圆围成的区域内，磁场的磁感应强度最小为

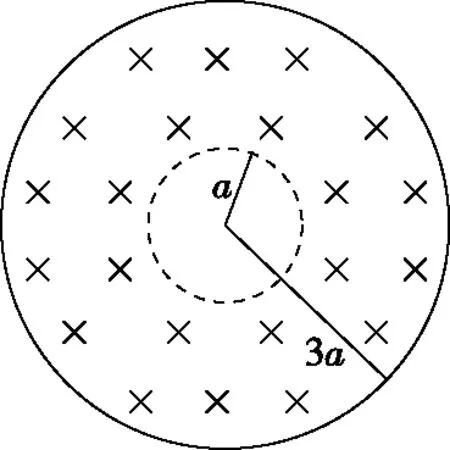
图1

( )

(2022·贵州适应性考试·18)如图2所示为一磁约束装置的简化示意图，内半径为a、外半径为3a的环状区域Ⅰ内有方向垂直纸面向里、磁感应强度大小为B的匀强磁场。小圆区域Ⅱ中有大量质量为m、电荷量为q的粒子在纸面内以不同速度向各个方向运动。要使所有粒子都不会穿出区域Ⅰ的外边缘，不计粒子重力及粒子间相互作用，则粒子的最大速度为

( )

二、分析对比

三、题目变式

【典例】内半径为R1、外半径为R2的环形区域中存在匀强磁场，带电粒子从S点射出，速度方向沿平面任意方向，大小不一。

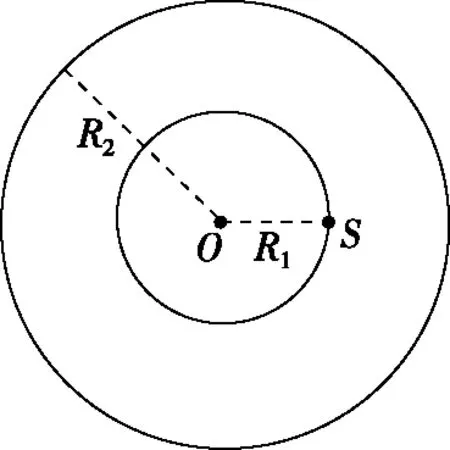
图3

【变式1】求最终不能射出磁场区域的粒子速率的最大值。

【变式2】若所有粒子都不能射出磁场，求入射粒子速率的最大值。

【变式3】从O点射出的粒子，速度方向沿平面任意方向，大小不一，求最终不能射出磁场区域的粒子速率的最大值(若所有粒子都不能射出磁场，求入射粒子速率的最大值)。

【变式4】从A点(AO=0.5R1)射出的粒子，速度方向沿平面任意方向，大小不一，求最终不能射出磁场区域的粒子速率的最大值。

【变式5】从A点(AO=0.5R1)射出的粒子，速度方向沿平面任意方向，大小不一，若所有粒子都不能射出磁场，求入射粒子速率的最大值。

【核心要点】若入射粒子在磁场中运动速度的大小和方向都不相同，那么粒子的运动轨迹圆既要缩放又要旋转。求解思路为先定方向，再逐个研究。磁场对带电粒子的约束需要判断研究对象是“某一个”粒子还是“每一个”粒子，若是约束“某一个”粒子，则要求某一个粒子不能射出磁场，求这个粒子的最大半径；若是约束“每一个”粒子，则要求所有粒子都不能射出磁场，求这群粒子的最大半径。取部分特殊入射方向作图，如图4所示。

图4

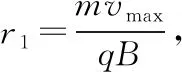
【变式3分析】当粒子从O点射入磁场时，粒子在内圆中都做匀速直线运动后，沿半径方向射入环形磁场，取一个方向研究，即定向不定径，故为放缩圆，作图如图5所示。

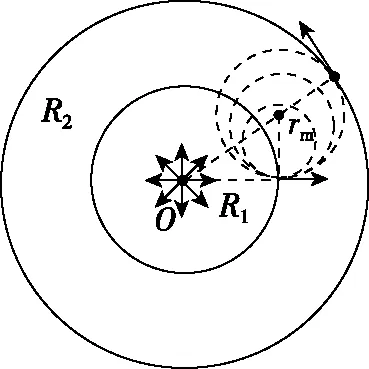
图5

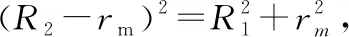
【变式4、5分析】通过变式3的分析，对比变式4和变式5，从A点(AO=0.5R1)射出的粒子都在内圆中做匀速直线运动，但进入环形磁场的情况都不一样，作图如图6、图7所示。

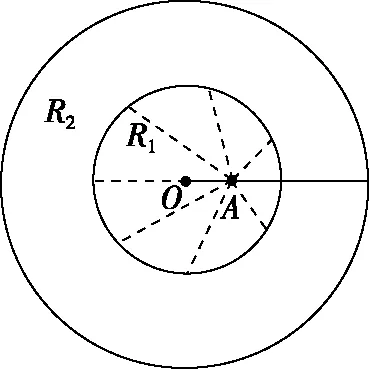
图6

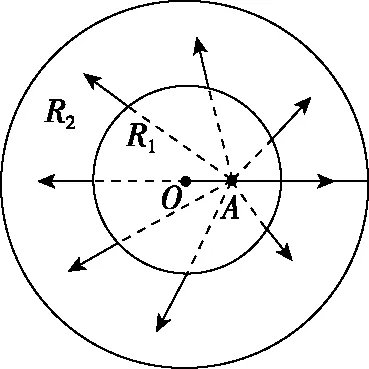
图7

由图8可知，由于粒子入射速度的方向与内圆半径的夹角是变量，则需探讨夹角变化情况。

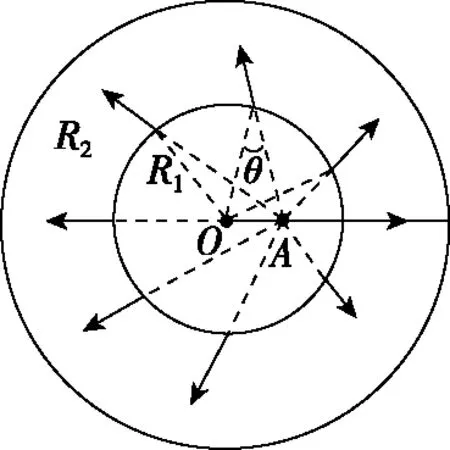
图8

故θ∈(0°，30°)，说明粒子射入磁场时的速度方向与内圆半径的夹角范围是0°～30°

仍选取其中一个点来研究，作图如图9、图10所示。

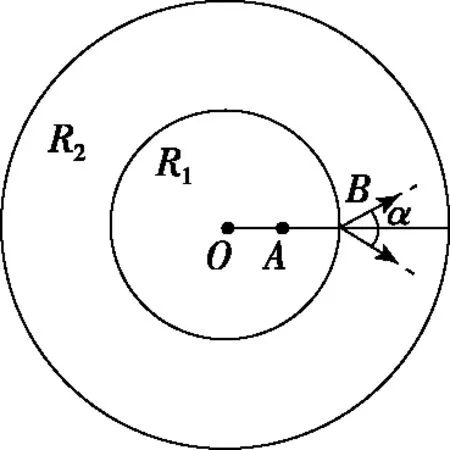
图9

图10

粒子射入磁场时的速度方向与内圆半径夹角的范围是0°～30°，故α=60°，分别做两个极限速度的轨迹圆，如图10所示，当约束的是“某一个”粒子时，最大半径为r2；当约束的是“每一个”粒子时，最大半径为r1。设轨迹圆半径与外圆半径的夹角为β，由余弦定理可得

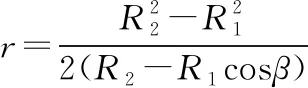
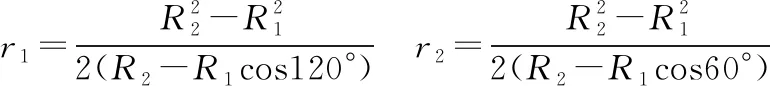
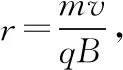
【归纳总结】解决该类磁约束问题，首先要判断研究对象是“某一个”还是“每一个”带电粒子，然后先定方向，逐个研究，再由临界相切找出极大值。若研究对象为“某一个”粒子，则找出临界最大半径即可求出最大速度；若研究对象为“每一个”粒子，则应找出临界相切半径的最小值，否则角度改变必有粒子射出磁场。2022年贵州省适应性考试第18题就是在2020年全国卷Ⅲ第18题的基础上进行的改编，2020年全国卷Ⅲ第18题对应变式3，2022年贵州省适应性考试的18题对应变式2，从学生反馈的情况来看，依然存在对知识理解不深，不懂得变通而无从下手的情况。笔者下面再以2022年八省联考T8第10题为突破口，进行分析。

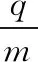
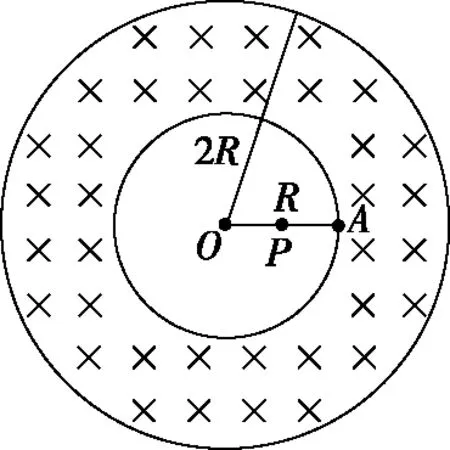
图11

( )

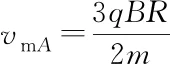
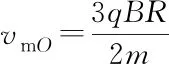
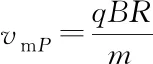
【说明】笔者认为，该联考题中“被约束相关量”的说法不够严谨，从题给选项来看，应改为“被约束的某一个粒子的相关量”，希望通过本文能和大家共同探讨这个问题。

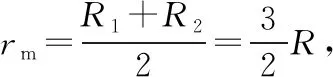
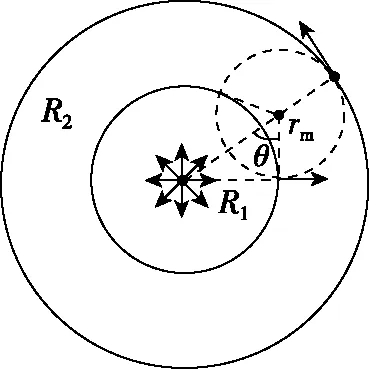
图12

【答案】ACD

【点评】环形磁场是有界磁场中比较难的模型，作为T8联考的压轴选择题，难度非常大，本题以“磁约束”为情境载体，数理分析为方法引领，从物理规律出发，结合数学知识找临界、求极值；本题对环形磁场这一模型的考查非常全面，要求学生熟练掌握带电粒子在匀强磁场中的“放缩圆”和“旋转圆”模型，也要求学生在处理物理问题的同时，要具有敏锐的数学“嗅觉”，能够根据相关物理量的不确定性，联系到余弦定理、均值不等式等数学手段。本题还可以对研究对象(“某一个”或“每一个”粒子)进行改编，是一道提升模型构建能力、培养科学思维素养的优质题。

四、教学启示

带电粒子在有界磁场中的临界问题是典型的运用数学知识处理物理问题的体现，本文中的真题及变式的难度梯度不同，对学生的能力要求也不同，尤其是变式4和变式5，可以用在二轮或冲刺阶段的训练中，从而强化关键能力，落实物理核心素养。

2020年取消考试大纲，命题无范围，试题的命制更灵活。但现在的命题仍然是2019年高考考试大纲界定的考试范围以及能力要求，虽然不同省份的能力要求有所不同，但对物理学科的能力的要求依然不变，即理解能力、推理能力、分析综合能力、应用数学处理物理问题能力、实验探究能力。近几年高考试题对数学能力的要求加强，包括应用数学图像描述物理过程或物理状态的变化，以及物理建模过程，都包含了大量的数学问题，而数学问题和物理问题相结合，成了最困扰学生的问题。在平时的教学中，笔者发现单独的数学问题学生能处理，而将数学问题应用到物理情境中时，学生就解决不了。笔者认为，主要还是因为传统教学过于注重解题技巧和解题经验，没有通过对学科知识的学习，养成运用数学知识处理物理问题的习惯和思维。作为一线教师，不应照本宣科，要带领学生深入研究习题，将机械地学习和解题转化为深层的构建，同时要淡化解题中的特殊技巧，注重原理中的通性通法，重视学生关键能力的培养，提高学生的学科素养，深层次地培养学生的思维，从而使学生能够处理灵活多变的问题。