基于高斯混合模型的非高斯振动疲劳频域求解方法

朱帅康，董龙雷，官 威，王 珺，李斌潮

(1.西安交通大学 航天航空学院，西安 710000；2.西安航天动力研究所，西安 710100)

机械结构的设计阶段，通常使用频域方法估计结构的疲劳寿命。当结构的应力响应服从窄带高斯分布时，可假设雨流计数的幅值服从Rayleigh分布，再结合Miner累计损伤准则[1]及材料的S-N曲线计算出结构的疲劳寿命。如果应力幅值为宽带信号，Rayleigh分布假设不再适用，许多学者提出了针对宽带载荷的算法，如Wirsching-Light(WL)方法[2]，Dirlik方法[3]，Zhao-Barker(ZB)方法[4]，Tovo-Benasciutti(TB)方法[5]等，这些方法都要求载荷为高斯随机载荷。

然而，许多随机载荷具有较强的非高斯特性，如风载、海浪冲击等，这些载荷产生的响应通常也呈现出非高斯性。比如，海浪对平台的冲击载荷峭度值大约为5，而风载的峭度值可能超过10。另外，还有一些载荷呈现多峰分布[6]，如桥梁、路面上的车辆载荷等。在不满足单峰高斯分布载荷的条件下使用频域疲劳计算方法，势必会带来较大的计算误差，产生错误的疲劳寿命估计。

针对非高斯载荷，Braccesi等[7-8]提出了修正系数法，其修正系数由非高斯分布的峭度值确定。这种方法只能用于单峰非高斯分布载荷，且要求无偏斜。Winerstein[9]建立了非线性变换模型，使用Hermiter多项式将非高斯过程转化为高斯过程，并且假设转换前后的功率谱密度保持不变，适用于载荷的非高斯特性不强的情形。另外，Wolfsteiner等[10-11]将一个非高斯过程分解为几个高斯过程，该方法要求非高斯分布无偏，且计算过程涉及到了应力功率谱的前8阶距，实际应用中可能会产生严重的计算稳定性问题。

综上所述，在多峰非高斯载荷下，目前还没有通用的疲劳计算方法。本文针对多峰非高斯载荷，使用高斯混合模型(Gaussian mixture model,GMM)对载荷进行描述，为了满足计算速度与精度，使用EM算法对模型参数进行求解，并结合TB方法得到多峰非高斯载荷下的结构频域疲劳计算方法。通过一个疲劳分析示例验证了该方法的有效性，表明该方法有更好的适用性及精度。

1 信号的非高斯特性

对于单峰的非高斯载荷，使用峭度值及偏度值可以对其进行描述[12]。对于一个高斯过程，其峭度值与偏度值分别为3和0。通常使用峭度值、偏度值与3和0的偏离程度衡量一个信号的非高斯性，且两者可同时存在。其中，偏斜度用来衡量信号的非对称性，如偏度值大于零则表示有更多的值分布在均值右侧，如图1所示。而峭度值描述信号在均值附近的密集程度，如峭度值大于3则表明仅有较少的值分布在均值附近，这意味着比起高斯分布，该信号有更高的“尾部”，如图2所示。

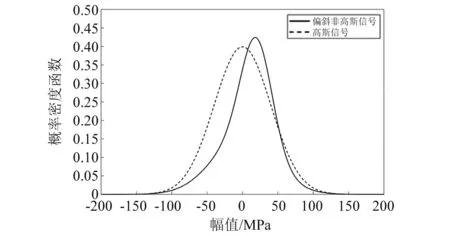
图1 偏斜非高斯信号Fig.1 Skew non Gaussian signal

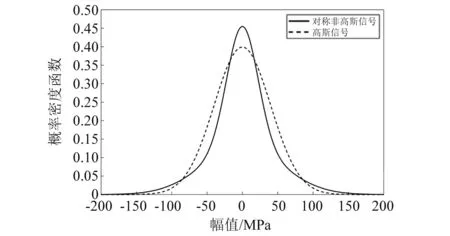
图2 对称非高斯信号(峭度值>3)Fig.2 Symmetric non Gaussian signal (kurtosis>3)

另外，一些载荷信号呈现双峰非高斯分布[13]，如一些桥梁上既有普通车辆也有重型车辆，且有许多样本点远离均值，呈现出明显的非高斯性，如图3所示。

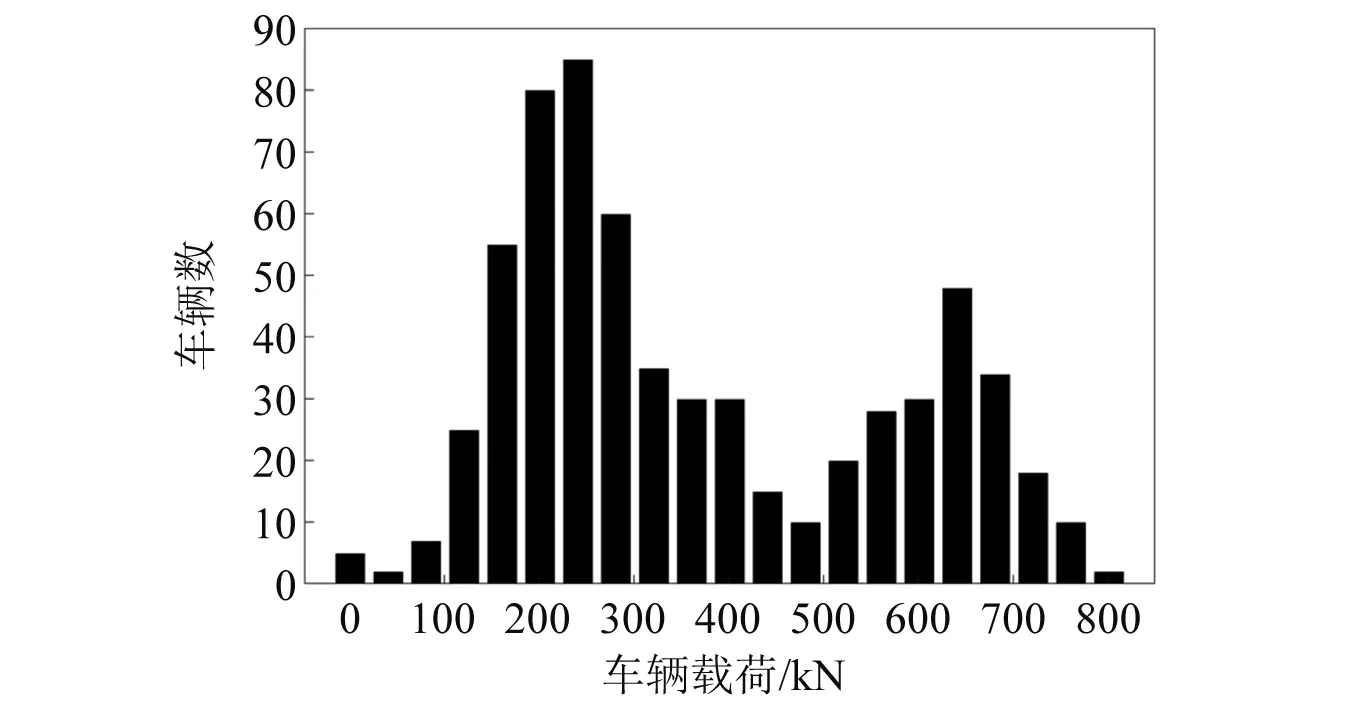
图3 桥梁上呈现双峰分布的车辆载荷Fig.3 The vehicle bi-modal load on the bridge

信号的非高斯特征会对疲劳计算产生影响，在单轴应力状态下，一个峭度值大于3的应力分布会对结构造成更大损伤。因为比起高斯信号，峭度值大于3的信号大幅值的应力循环更多。偏度值也会对疲劳计算产生影响，但是依赖于所选取的平均应力修正方法，且对计算结果的影响不如峭度值明显。

2 高斯混合模型及EM算法

2.1 高斯混合模型

GMM可将一组数据的概率密度函数分解为多个高斯函数概率密度的线性组合

(1)

式中：xi属于数据点X={x1,x2,…,xN}；αj为加权系数，且满足

(2)

由于载荷数据为一维数据，G(xi;μj,Σj)为一维高斯分布函数，表达式为

(3)

将G(xi;μj,Σj)称为GMM的第j个高斯分量，μj和Σj分别为此高斯分量的均值与方差。

理论上可以使用GMM描述任意分布的概率密度函数。程红伟等[14]建立了二阶的GMM，由于二阶高斯混合模型未知参数较少，文中使用了高斯分量的前6阶矩进行模型求解。当载荷呈现出多峰分布时，需要的高斯分量随之增多，文中的求解方法不再适用，因此引入EM算法进行参数求解。EM算法本质上为一种迭代算法，对于有多个高斯分量的GMM，使用极大似然估计往往无法获得参数的解析解，因此通过迭代来间接获得各参数值。

2.2 EM算法

EM算法引入一组隐变量Zi={zi1,zi2,…,zik}，代表数据属于各个高斯分量的概率

(4)

将(X,Z)称为完整数据，其最大似然函数为

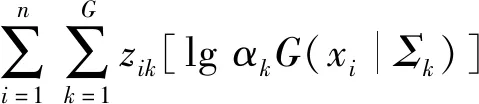
(5)

EM算法可分为E步与M步，E步即为求期望(expectation),M步为求极大(maximization)。

E步：已知观测数据X及估计参数θi，求其隐变量的对数期望

(6)

(7)

M步：求Q(θ|θi)的极大值

(8)

可以求得，高斯分量的权系数为

(9)

高斯分量的期望向量为

(10)

高斯分量的方差为

(11)

通过上述过程，即可实现θi→θi+1的迭代。选择终止迭代条件，可以计算隐变量的对数期望，即式(6)中的Q值，当Q值逐渐增大趋于稳定时则认为求得的参数收敛，停止迭代。

3 GMM-TB求解方法

3.1 Tovo-Benasciutti方法

Tovo和Benasciutti在2005年提出了一种计算疲劳损伤的方法，文中将疲劳损伤强度的上限与下限线性组合，从而计算出疲劳损伤，基于TB方法得到的疲劳损伤值为

(12)

式中：C和m为材料常数，由S-N曲线确定；vp为峰值密度，由式(13)确定

(13)

ξi为单边功率谱Gxx(f)的第i阶矩，表达式为

(14)

b为权重系数

(15)

参数βi用来估计谱宽度，表达式为

(16)

Γ(·)为欧拉伽马函数，具体表达式如下

(17)

该方法在疲劳寿命计算中由许多研究证明有良好的计算精度[15-17]。

3.2 GMM-TB求解方法

对于一个非高斯过程而言，其功率谱密度曲线无法描述其非高斯特性。由GMM可以确定多个高斯分量出现的概率，因此可以根据GMM对功率谱密度进行分解。

GMM中第i个高斯分量的方差可以表示为

(18)

式中，Gi(f)为第i个高斯分量的功率谱密度。

非高斯过程X(t)的方差可以表示为

(19)

(20)

将式(18)和式(19)代入式(20)得到

(21)

假设Gi(f)沿频率轴与GX(f)成比例关系，则Gi(f)可由式(22)确定

Gi(f)=λiGX(f)

(22)

式中，λi为比例系数，可以联立式(18)、式(19)、式(22)得到

(23)

将式(22)、式(23)代入式(21)即可得到非高斯过程的功率谱密度的分解形式。

使用功率谱密度(power spectral density，PSD)计算疲劳损伤时，平均应力的影响可通过式(24)修正

GiT(f)=c2(σm)·Gi(f)

(24)

式中，c(σm)为平均应力修正系数，可由Goodman修正公式确定

(25)

式中：σm为平均应力；Rm为材料的拉伸极限强度。

通过以上步骤，可以确定GiT(f)，代入式(12)，通过TB计算方法得到对应损伤值，记为Di。总损伤值可由式(26)确定

(26)

从而得到疲劳损伤计算的GMM-TB计算公式

(27)

4 示 例

4.1 信号生成

首先，需要生成一双峰分布的非高斯随机信号，生成过程如下，首先确定生成随机信号的功率谱密度，然后根据傅里叶逆变换，随机信号的相位服从[0,2π]的均匀分布，信号的非高斯性可利用零均值非线性函数得到[18]，将峭度值设为5，记为x1(t)。之后将均值取为240 MPa,再生成一组随机信号，其峭度值为10，记为x2(t)。将两信号叠加，即可得到服从双峰分布的非高斯载荷信号，记为xng(t)，生成的双峰非高斯随机载荷如图4所示，其功率谱密度如图5所示。生成信号的具体特性由表1列出。该信号线性坐标及对数坐标下的概率密度分布如图6所示，为了显示该信号的非高斯性，图中也显示了相应高斯分布的概率密度曲线。

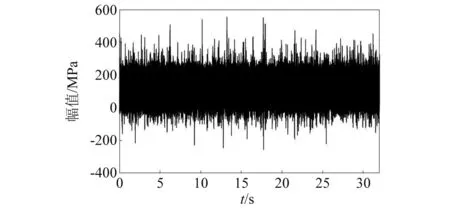
图4 双峰非高斯信号Fig.4 Bi-modal non Gaussian signal

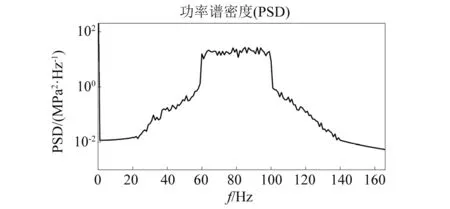
图5 双峰非高斯信号的功率谱密度曲线Fig.5 Power spectral density of bi-modal non Gaussian signal

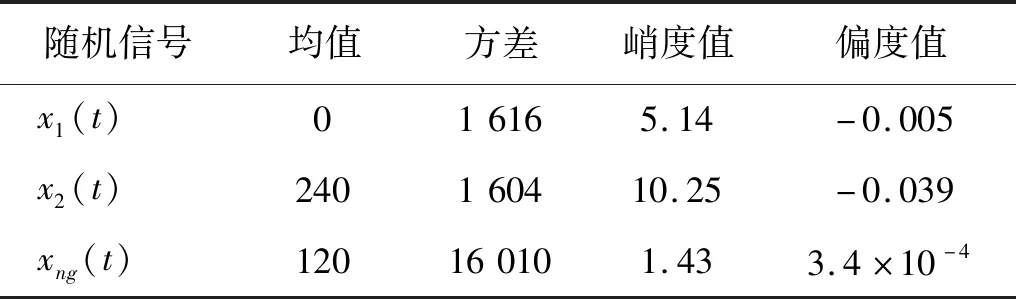
表1 非高斯载荷信号参数Tab.1 Non-Gaussian load signal parameters

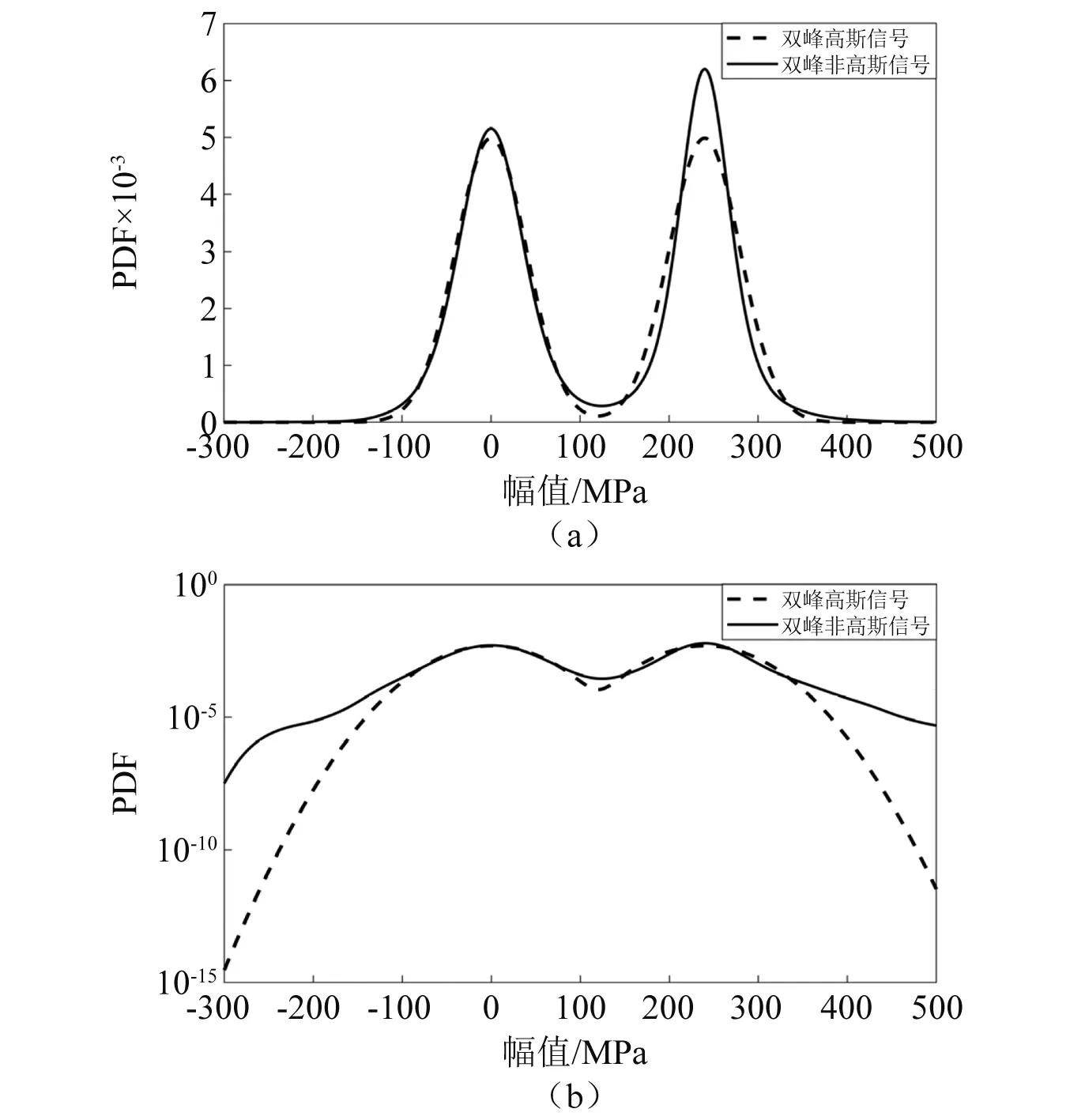
图6 双峰非高斯分布信号的概率密度曲线Fig.6 PDF of bi-modal non Gaussian signal

由图6可知，比起高斯分布，该信号有着明显更高的“尾部”，说明其大幅值载荷出现的概率更大，从而对结构造成的损伤也更大。

4.2 寿命计算及结果分析

材料的一些属性，如S-N曲线斜率等，也会对疲劳寿命的预测精度产生较大影响。为了对方法的验证具有一定普遍性，选取了三种材料，其S-N曲线的斜率分别取为3、4、6。材料属性如表2所示，C为S-N曲线材料常数，Su为材料的拉伸极限强度，k为材料的S-N曲线斜率。

表2 用于疲劳计算的材料参数Tab.2 Material parameters for fatigue life calculation

按照上述EM算法流程，使用python语言对该信号进行GMM参数估计，选取一组GMM的初始值，对参数进行迭代，表3给出了当K=4时参数α的迭代结果。可以看出，随着迭代次数的增加，参数的估计结果逐渐平稳，Q值的变化如图7所示，也逐渐增大直至平稳。此处选取迭代50次的参数值作为GMM的估计值，在实际应用中可以增加迭代次数直至参数的估计结果趋于稳定，从而使估计值与真实值的误差足够小。

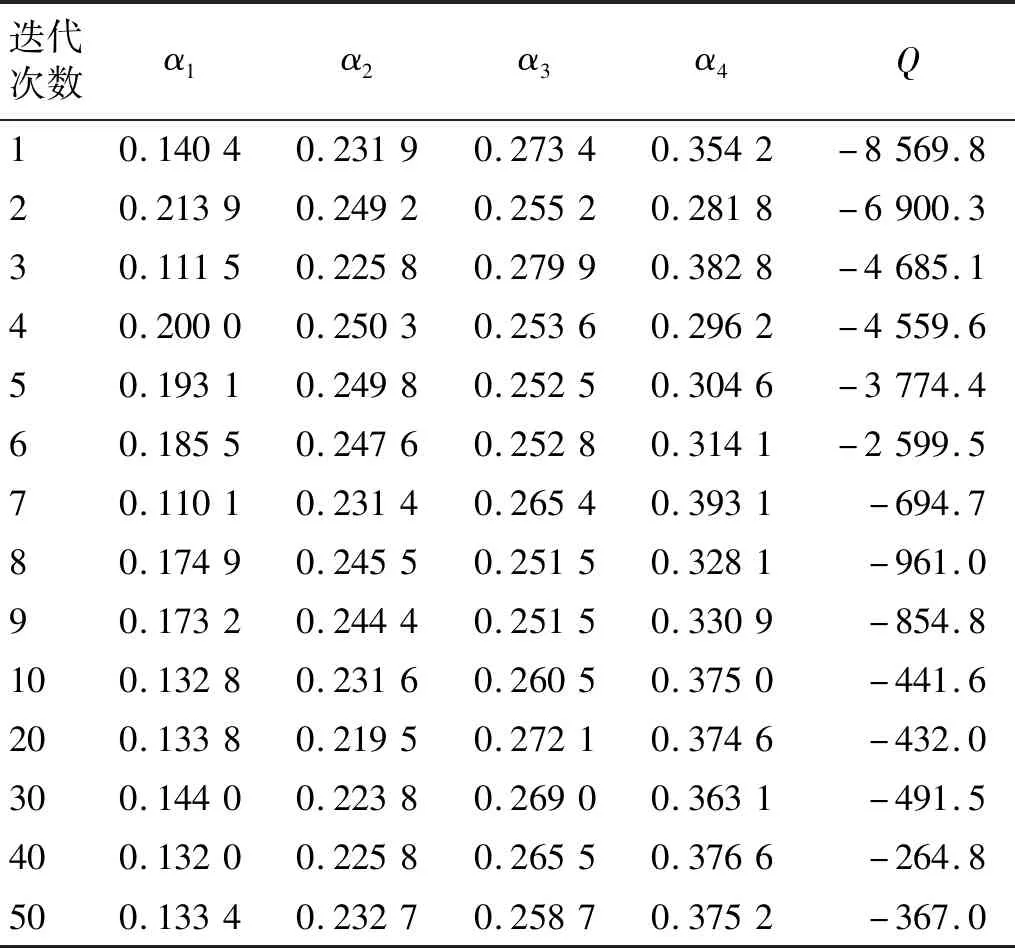
表3 EM算法估计GMM参数值的数值迭代结果(K=4)Tab.3 Numerical iteration results of EM algorithm for estimating of GMM (K=4)

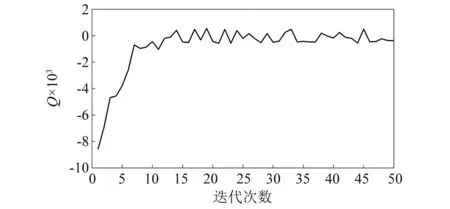
图7 Q值随迭代次数增加的变化曲线Fig.7 The Q value with the increase of iteration times

由K=2开始逐渐增大K值至10，得到不同高斯分量的GMM。图8给出了K=2，K=4，K=6，K=8，K=10时GMM的概率密度曲线，为了更好地显示拟合效果，以对数坐标显示。图9给出了不同分量的GMM在大幅值处对原信号的拟合效果，结果显示随着分量数的增多，拟合效果逐渐变好。当K=2时，即两个高斯分量时，GMM无法准确描述该双峰信号，随着K值增大，在信号两侧，载荷大幅值处，GMM与原信号的吻合程度更好。

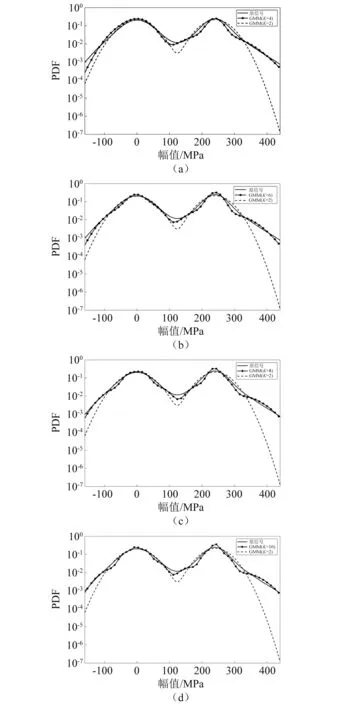
图8 对数坐标下不同K值GMM的概率密度曲线Fig.8 PDF of GMM with different K values in logarithmic coordinates

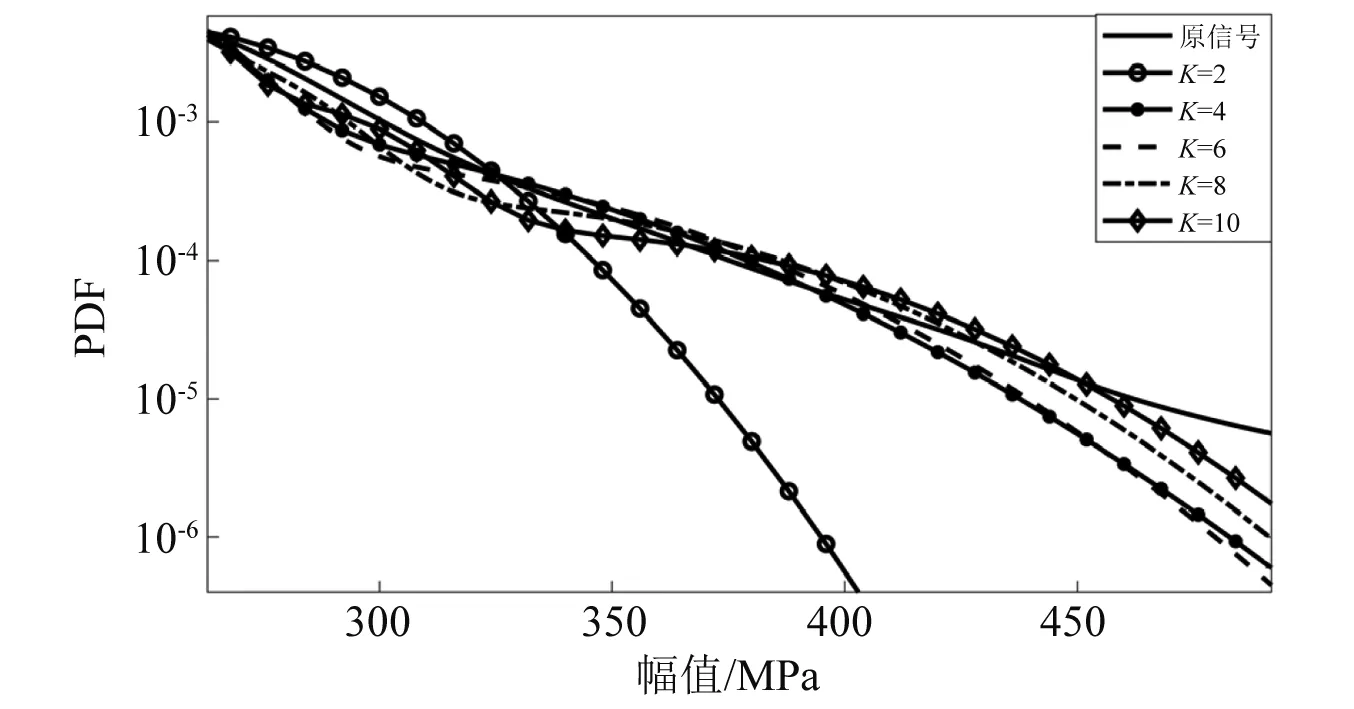
图9 大幅值区域GMM的概率密度曲线Fig.9 PDF of GMM models in large value region

得到不同K值下的高斯模型后，按照第3章中的计算方法，首先由式(22)、式(23)得到载荷功率谱密度的分解形式，再根据式(24)、式(25)进行平均应力修正，得到每个高斯分量的损伤值，由式(27)得到疲劳计算寿命。由于S-N曲线斜率变化较大，为了得到合理的寿命计算值，因此在不同的K值下，对初始信号的RMS值进行了选取。表4给出了K值由2～12下GMM的计算寿命及直接使用TB方法得到的疲劳寿命，并以雨流计数法得到的疲劳寿命作为参考[19]。图10将寿命的计算结果以图形显示，其中K=1代表不使用GMM，直接使用频域法得到的寿命结果。

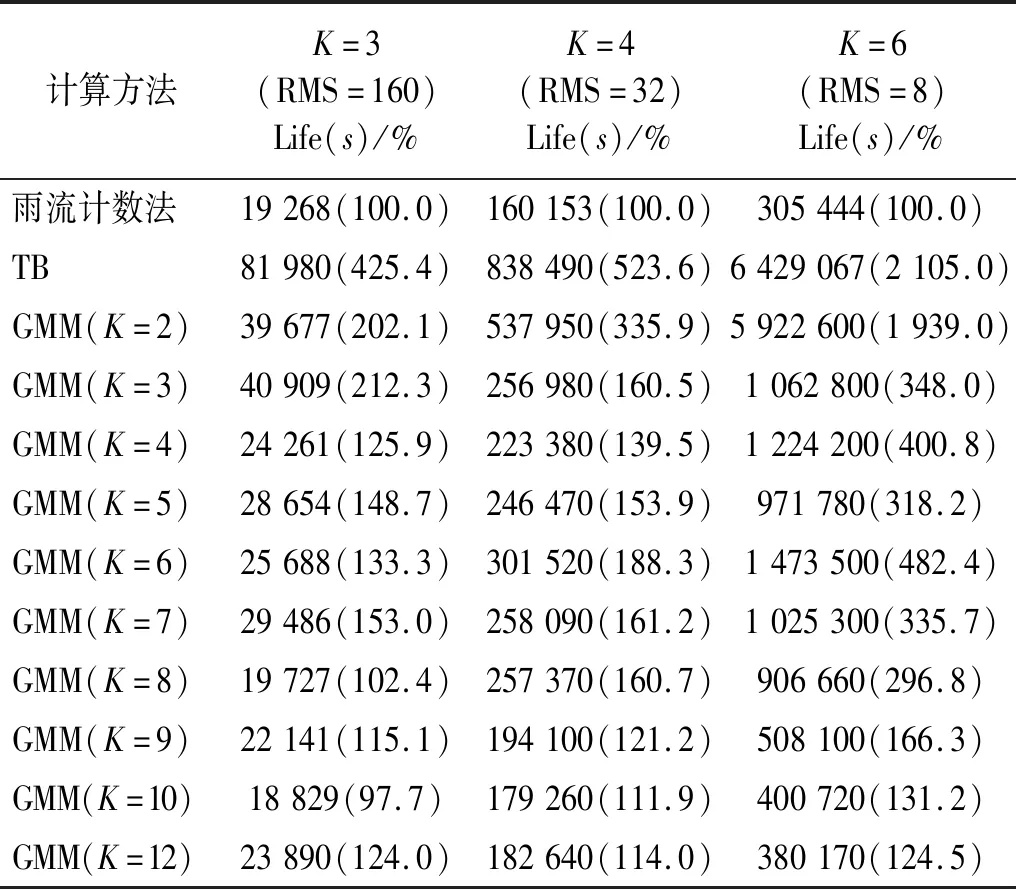
表4 疲劳寿命计算结果Tab.4 The results of fatigue life calculation

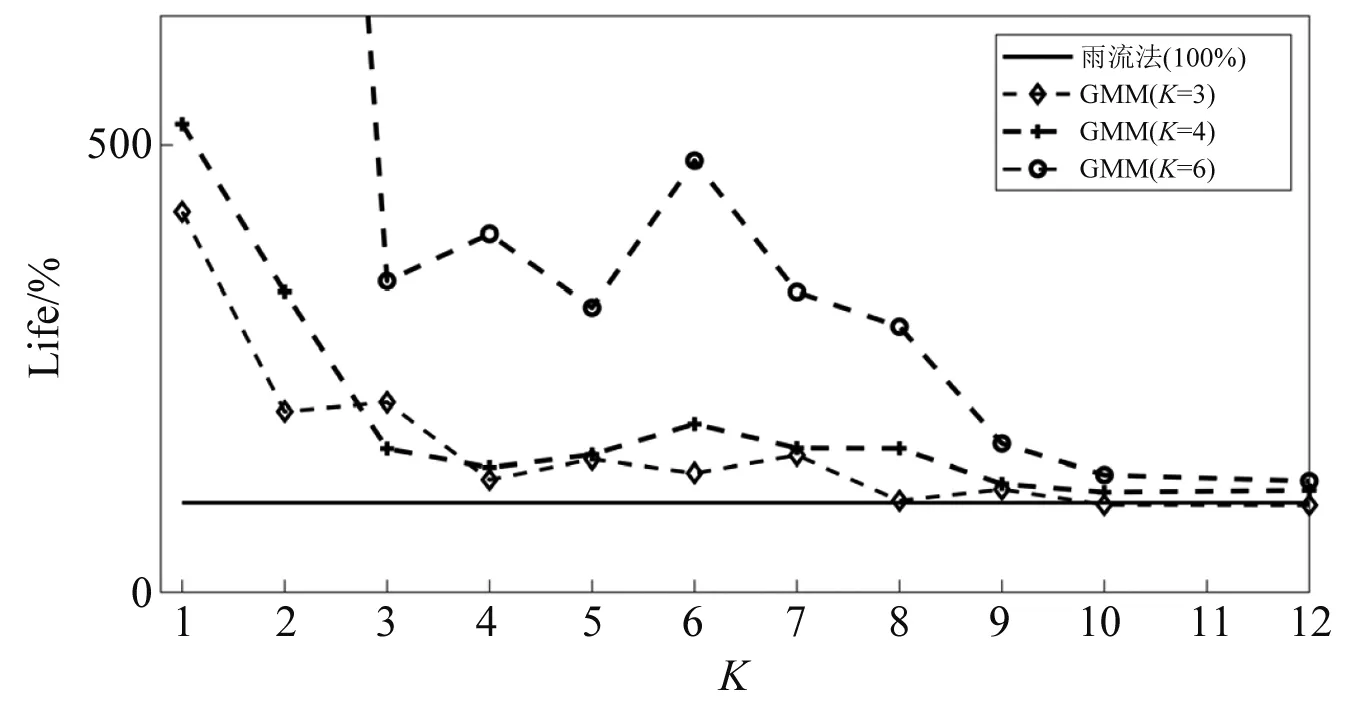
图10 不同K值下的疲劳寿命计算结果Fig.10 The results of fatigue life under different K

由计算结果可以看出，对于呈双峰分布的非高斯载荷，直接使用频域法得到的结果与实际值相差较大，因为频域法仅适用于单峰高斯载荷，且未进行平均应力修正；若将载荷分解为两个高斯过程，即K=2的GMM，考虑了载荷平均应力的影响，但无法描述峭度值对材料造成的损伤；随着K值增大，GMM中的高斯分量增多，载荷的非高斯特性被描述出来，得到的寿命结果也与真实值更加接近,材料S-N曲线斜率较小时，高斯分量取到10，其计算精度可控制在20%以内。材料S-N曲线斜率较大时，非高斯性对疲劳计算的影响更为显著，需要较多的高斯分量计算结果才可收敛。当继续增大K值，疲劳寿命的计算精度提高不明显，一方面由于当K值增大时，参数收敛变得困难，GMM参数求解的误差较大；另一方面GMM容易出现过拟合现象，K值很大时，出现了一些偏离原数据分布的高斯分量，致使计算精度变差。因此，实际进行疲劳计算时要合理选取GMM中高斯分量的个数。

5 结 论

本文提出了一种非高斯随机载荷下对结构进行疲劳计算的频域方法。首先引入GMM对载荷进行描述,并使用EM算法对模型参数进行求解，随着高斯分量的增多，GMM以准确描述单峰及多峰非高斯载荷。在此基础上对信号的功率谱密度进行分解，并结合Tovo-Benasciutti方法推导出一种多峰非高斯载荷下的频域疲劳计算方法。为了验证此方法，对一个双峰分布的非高斯载荷信号进行了疲劳分析，选取三种材料，以雨流计数法作为参考，结果表明对于双峰非高斯载荷，使用GMM可以明显提高计算精度，且在一定范围内，计算精度随高斯分量的增多而提高。非高斯性在材料S-N曲线斜率较大时对计算的影响更为显著，材料S-N曲线斜率较小时，高斯分量取至10附近，其计算精度可控制在20%以内，材料S-N曲线斜率较大时，计算所需的高斯分量较多，同时计算精度提升明显。另外，由于文中方法以Tovo-Benasciutti频域疲劳计算方法为基础，因此也适用于宽带随机载荷的计算，对工程问题具有一定实用价值。