磁阻旋转变压器等效电路及原边反射误差分析
刘德超,熊 建
(北汽福田汽车股份有限公司,北京 102206)
0 引 言
新型的磁阻式旋转变压器由于具有结构简单、 工作可靠、 体积小等优点在电机控制领域得到了广泛应用[1-3]。磁阻式旋转变压器主要分为定、转子两部分,均为矽钢片叠压而成。定子开槽,励磁绕组和正、余弦反馈信号绕组均以集中绕组的方式绕制在定子槽内,其中励磁绕组一般为等匝数逐齿反饶串接,正、余弦绕组按正、余弦分布规律逐齿绕制串接。转子无绕组,一般制作成特殊形状,使定、转子气隙磁导具有正弦变化规律,从而使得励磁绕组和正、余弦绕组的耦合磁导依据定、转子相对位置具备正、余弦变化规律,最终在旋转变压器输出端获得包含定、转子相对位置信息的正、余弦信号。
上面提到磁阻式旋转变压器的励磁绕组一般为逐齿反接串联,而正、余弦绕组则是逐齿按正弦分布规律绕制串接,故励磁绕组与信号绕组的耦合系数小于1,并不符合理想变压器条件,不可对磁阻式旋转变压器用理想变压器理论在电路中进行建模分析,所以下文在分别对励磁绕组的自感、信号绕组的自感以及励磁绕组和信号绕组的互感进行了详细分析计算的基础上,使用励磁绕组的自感、信号绕组的自感以及励磁绕组与信号绕组的互感建立旋转变压器的等效电路,并根据等效电路,分析磁阻式旋转变压器接入电路后,由于负载效应及阻抗匹配引起的解码误差。
1 绕组电感计算
磁阻式旋转变压器转子一般制作成特殊形状,使得气隙磁导包含直流分量、基波分量以及高次谐波分量,其中高次谐波分量一般是用来优化因绕组、齿槽等引起的输出端高次谐波电势。我们这里只讨论气隙磁导的直流分量和基波分量。气隙磁导的表达式如下:
(1)
式中,Λk为定子第k齿对应气隙磁导;Λm0为气隙磁导直流分量;Λm1为气隙磁导基波分量幅值;p为转子极对数;Θ为定转子相对位置电角度;αe为相邻两齿对应电角度。
(1)励磁绕组电感(信号绕组均开路)
为优化磁路,磁阻式旋转变压器的励磁绕组一般为等匝数逐齿反向绕制串接,设每个定子齿上的绕组匝数为N1,可得第k齿绕组电感为[4]
则励磁绕组总电感为
(2)
将式(1)带入式(2)可得:
由上述推导可以得到关于磁阻式旋转变压器励磁绕组自感的以下结论:
励磁绕组自感为一恒定值,并不受气隙磁导变化(即旋转变压器定、转子相对位置)的影响,只与气隙磁导的直流分量、绕组匝数以及定子槽数有关。
(2)信号绕组电感(励磁绕组及另外一组信号绕组均开路)
磁阻式旋转变压器的信号绕组采用正弦(或余弦)分布[5],每相绕组逐齿按正弦(或余弦)分布规律绕制串接,其分布周期一般为转子极对数的倍数,可用下式来表示信号绕组每齿匝数,其中为绕组分布匝数峰值。
Nsk=Nssin[(k-1)αe]
第k齿信号绕组电感可表示为
则可得信号绕组总电感为
(3)
因
联合式(1)和式(3)可得:
由上述推导可以得到关于磁阻式旋转变压器信号绕组自感的以下结论:
信号绕组自感为一恒定值,并不受气隙磁导变化(即旋转变压器定、转子相对位置)的影响,只与气隙磁导的直流分量、绕组分布匝数峰值以及定子槽数有关。
(3)励磁-信号绕组互感(以正弦绕组为例)
设定子每齿励磁绕组匝数为N1,每齿正弦信号绕组匝数Nsk=Nssin[(k-1)αe],则第k齿励磁绕组与正弦信号绕组之间的互感为
Mk=N1Nssin[(k-1)αe]Λk
因励磁绕组为逐齿反向绕制的,所以可得励磁绕组与正弦信号绕组之间的总互感为
(4)
式中,Ks为小于1的常系数,其与定子齿槽数、绕组嵌线方式(隔齿反接或逐齿正接)等相关。
可得,励磁绕组与正弦信号绕组之间的互感与气隙磁导的交流分量幅值、励磁绕组匝数、正弦信号绕组分布匝数峰值以及定子槽数、正弦信号绕组绕制方式有关,并且是与定、转子相对位置成正弦关系。同理可以推得励磁绕组与余弦信号绕组之间的互感与定、转子相对位置成余弦关系。
2 等效电路
上文中分别计算了磁阻式旋转变压器的励磁绕组和信号绕组的自感以及两者之间的互感,可以看出,虽绕制在同一铁心(定子)上,但因其耦合系数小于1,故不能作为理想变压器进行建模。
下面根据磁路耦合,将励磁绕组与信号绕组作为一组耦合电感,使用上文中计算所得励磁绕组自感L1、信号绕组自感L2以及两者互感M进行电路等效,具体电路如图1所示。

图1 旋转变压器等效电路
由图1可得方程组:
(5)
式中,L1为励磁绕组自感;L2为信号绕组自感;M为励磁绕组和信号绕组互感;R1为励磁绕组直流电阻与铁心损耗等效电阻之和;R2为信号绕组直流电阻与铁心损耗等效电阻之和;αe为相邻两齿对应电角度;ZL为负载阻抗。
由式(5)可得:
(6)
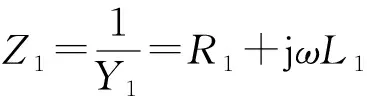
根据式(6),可分别对输入、输出进行等效如下。
(1)输入端等效(励磁端)
旋转变压器输入等效如图2所示。

图2 旋转变压器输入等效
Z1=R1+jωL1
Z12=(ωM)2Y2
(2)输出端等效(信号端)
旋转变压器输出等效如图3所示。

图3 旋转变压器输出等效
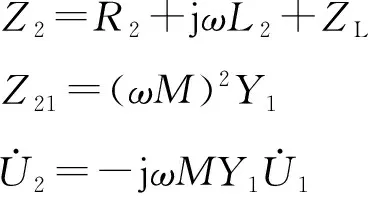
(7)
由式(7)可知,信号端开路输出电压是正比于互感M的,又由式(4)可知,互感M与旋转变压器转子位置相关,所以可得信号端开路输出电压:
式中,K为一常系数,可对应旋转变压器的变比参数。
3 误差分析
在旋转变压器信号绕组接入负载后,对正、余弦信号进行解码时,我们均是假定负载所得有效信号为正比于开路输出电压的信号,另设定:
●正弦信号绕组自感为Ls,余弦信号绕组自感为Lc,且Ls=Lc=L2。
●励磁绕组与正弦信号绕组互感为Ms=MsinpΘ、励磁绕组与余弦信号绕组互感为Mc=McospΘ。
●励磁绕组自感为L1,励磁绕组内阻为R1。
●正弦信号绕组内阻为Rs,余弦信号绕组内阻为Rc,且Rs=Rc=R2。
(8)
但由图3可以看出,在旋转变压器信号绕组接入负载后的等效电路中,引入了一项与励磁绕组阻抗及互感M相关的阻抗项Z21,我们称之为励磁绕组到信号绕组的反射阻抗。Z21是随着旋转变压器定、转子相对位置变化而变化的,其会造成负载上的有效信号相对于开路输出电压信号产生偏移,下面利用上述等效电路,分析当旋转变压器接入负载后,反射阻抗Z21的变化对负载ZL两端得到的有效信号的影响。
由图3所示等效电路可得负载ZL上实际所得有效电压为
(9)
则:
因,Ms=MsinpΘ,Mc=McospΘ,设Z=(ωM)2Y1
则:
(10)
(11)
可得:
(12)
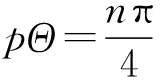
此时误差为0。
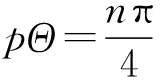
或
此时误差最大。其中,Z=(ωM)2Y1。
由式(12)可知,由励磁绕组反射阻抗产生的误差可以作为正、余弦信号的幅值失配误差进行考虑,则该误差为[6]
(13)
其中,δ为幅度失配百分比,即:
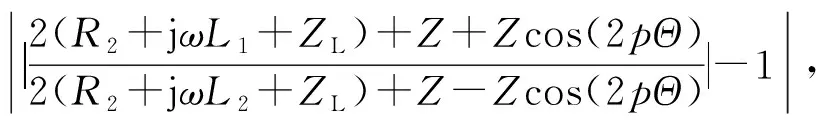
虽然由励磁绕组反射阻抗引入误差的频率为转子电角频率的4倍,但误差涉及复数域计算,解析解较复杂,下面计算励磁绕组反射阻抗引起幅度失配百分比δ的取值范围,为δ确定一个极值。
前文已提到当cos(2pΘ)=±1时,



故可得:


4 设计实例
前文已提到,每0.3%的失配幅度,对于12位RDC将产生大约1LSB的误差。若要将因反射阻抗引入的误差控制在1LSB以内,则需要将反射阻抗引入的幅度失配控制在0.3%以内,为提高裕度,我们以反射阻抗所能引起的失配幅度极值作为设计输入,即
δmax≤0.3%
以一款批量应用的旋转变压器规格书参数为设计输入,如表1所示。
(1)计算绕组自感、互感
励磁绕组自感:
信号绕组自感:
互感峰值:
M=0.286×L1=0.000531=531 μH
(2)计算反射阻抗
励磁阻抗反射至信号绕组阻抗:
(3)计算负载
因旋转变压器的负载一般为芯片引脚,输入阻抗非常大,近似开路,所以电路中用于滤波的电容作为主要负载对象,即图 4中的C76,C80,C172,C174,C176。

图4 实际应用电路

由
得:ZL≥3552.8,即C≤4.48 nf。故在正余弦信号所接后级负载电路中,用于共模及差模滤波的电容值最大不要超过4.48 nf(图3中为C172//C176+C76//C80+C174),则由反射阻抗引起幅值失配造成的误差在12位RDC中不超过1LSB。
5 结 论
本文详细分析了旋转变压器励磁、信号绕组的自感、互感,并使用励磁绕组、信号绕组的自感、互感导出旋转变压器的等效电路,然后根据等效电路引出由反射阻抗引起的解码误差,最后根据一款实际应用的旋转变压器,计算达到所需解码精度所使用的滤波电路容值限制,为旋转变压器的应用电路设计提供理论参考及实际案例。

