基于全局解析-模拟退火算法的外转子永磁风力发电机优化设计
周晓燕,王德鹏,唐 旭,王金平
(1.青岛理工大学 信息与控制工程学院,山东 青岛 266520;2. 青岛麦克斯韦电机科技有限公司,山东 青岛 266000)
0 引 言
永磁电机解析模型的建立已有很多学者做过研究[1-8],本文以一台表贴式外转子永磁风力发电机为样机建立了全局解析模型其中在气隙区域建立了拉普拉斯方程,在槽区域和永磁体区域建立了泊松方程。以上偏微分方程可利用分离变量法求解进而得到傅里叶级数形式的解析解。
齿槽转矩会引起永磁风力发电机启动时的诸多问题,因此为提升电机性能应使发电机齿槽转矩降低到最小。通过改变电机磁极参数、改变电枢参数、合理选择电枢的槽数和极数等传统优化方法来优化电机可达到减小齿槽转矩的目的。但随着多目标智能优化算法的迅速发展也有很多学者将遗传算法、粒子群算法和蚁群算法等智能算法引入到电机设计中来[9-13]文献[9]中以有限元法分析为基础,利用MATLAB和ANSYS平台建立了基于聚合函数的新型力矩电机多目标优化模型。提出一种变权重免疫克隆选择算法(VW-ICSA),用VW-ICSA对上述模型进行求解并对电机参数进行了优化。结果表明优化后的参数更符合设计要求。文献[10]提出了一种基于熵值权重的永磁驱动器多目标优化函数,在磁场解析模型的基础上对永磁涡流驱动器的输出转矩、转动惯量和驱动器体积应用多种群遗传算法进行了优化设计,虽然优化效果比较明显但该算法存在易早熟而陷入局部最优解的缺陷。文献[11]中先利用解析算法构造了一种球形永磁电机气隙磁密的解析模型在此基础上以基波幅值和波形畸变率为优化目标,采用粒子群算法对六极永磁体阵列进行了多目标优化优化设计,但是该算法存在全局寻优能力差且易陷入局部最优解的缺点。文献[12]针对异步电机采用铜转子而造成的起动转矩变小,起动电流变大的问题,提出一种混沌粒子群算法来优化电机结构并取得了良好的效果。当然,智能算法在对目标优化过程中也会出现计算量大、收敛速度慢等亟待解决的问题[13-17]。
有限元算法等传统电磁场计算方法虽具有精度高,可处理材料非线性等优点但不能直接反映电磁性能与设计参数之间的物理关系,因此无法结合现代智能优化算法对电机模型进行优化设计。然而解析算法能够清晰的反应电机设计参数与电磁性能之间的关系且具有运算时间短、速度快等优点,故可以结合现代智能优化算法对电机进行优化设计。本文以一台外转子永磁风力发电机为研究对象,首先建立了其齿槽转矩解析模型然后运用全局解析-模拟退火算法对其进行了优化设计同时克服了其他算法全局搜索能力差易陷入局部最优解的缺点,实验结果证明电机优化之后齿槽转矩得到了明显的降低。
1 极坐标下外转子永磁风力发电机二维几何模型及其解析建模
1.1 原电机解析计算二维几何模型
选用一台额定值为5 kW、400 V、100 r/min的20极72槽表贴式外转子永磁风力发电机作为计算与试验样机。二维极坐标下样机的几何模型如图1所示。

图1 外转子永磁风力同步发电机剖面图
原电机解析计算二维几何模型的基本参数如表1所示。
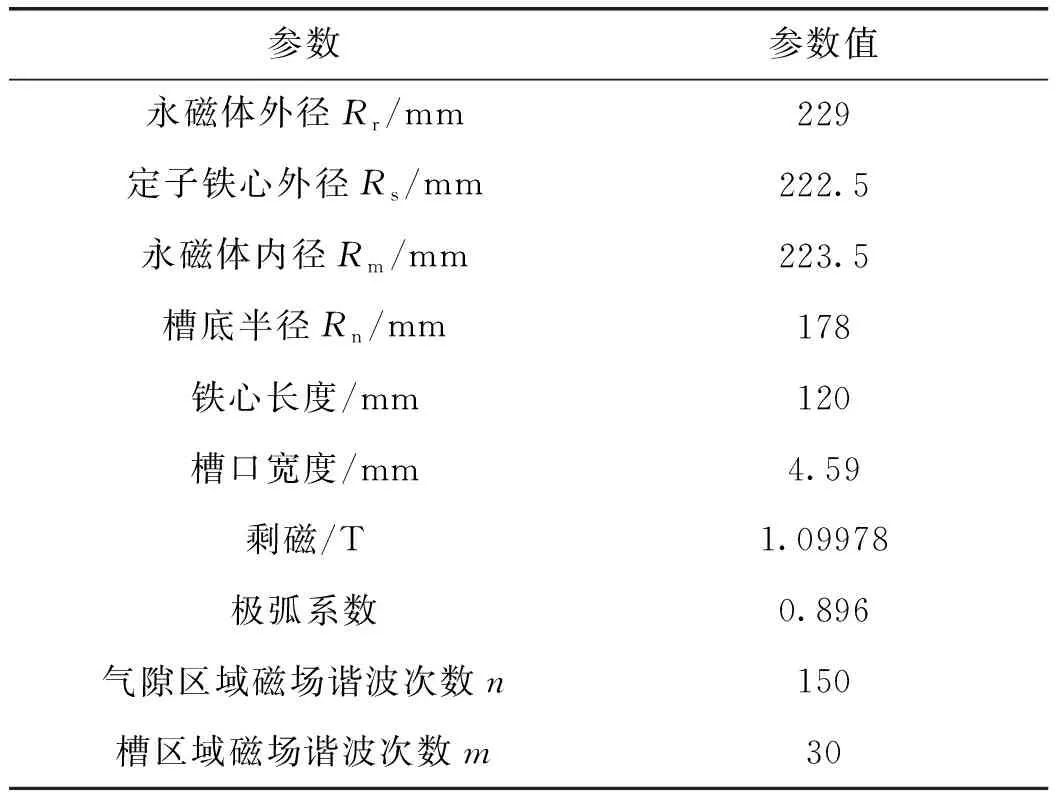
表1 电机模型基本参数
表贴式永磁电机的定子铁心内表面开槽后会对气隙磁场造成很大的影响,相关研究表明这种影响主要是由于开槽时槽口的形状和大小决定的。因此本文在解析建模过程中是将实际的槽型简化为跟槽口宽度相等的直槽且槽深保持不变,简化后的模型在二维极坐标下的剖面图如图2所示。

图2 简化后外转子永磁风力发电机剖面图
1.2 原电机解析计算模型建立
根据外转子风力电机内部结构特点及材料属性将内部电机区域划分为气隙区域Ⅰ、永磁体区域Ⅱ以及槽区域Si(i=1,2,3…Q)如图3所示。

图3 电机内部磁场区域建模划分
1.3 原电机解析计算模型的建立
空载情况下,气隙区域I、永磁体区域II第i个槽区域Si的矢量磁位方程为
气隙区域:
(1)
永磁体区域:
(2)
式中,γ为磁阻系数,M为永磁体磁化强度矢量。
槽区域:
(3)
其中:
根据分离变量法解出外转子永磁电机气隙区域、永磁体区域、第i个槽区域Si的通解如下[4]:
(4)
(5)
式中,m表示极对数p和槽数Q的最大公约数。
(6)
(7)
(8)
(9)
且由:
(10)
(11)
(12)
同理BrII、BθII、BθSi可求得[4]。应用Matlab符号运算功能结合边界条件可解的气隙区域、永磁体区域矢量磁位表达式系数AIn、AIIn等[4]。
2 电机空载时各参数的解析计算及实验验证
2.1 空载磁场的计算
由空载气隙磁密的切向分量和径向分量解析表达式,编写Matlab程序计算空载气隙磁密的切向分量和径向分量。利用高精度仿真软件Motorcad在相同参数条件下建立电机模型并进行空载气隙磁场切向分量和径向分量的计算,并将计算结果与解析法对比。结果如图4所示。

图4 空载气隙磁密解析波形与有限元波形比较
图4中曲线的下凹是由定子槽引起的磁通密度下降导致的,齿边缘聚磁效应的存在会使得切向和径向磁密波形的齿边缘出现磁密尖峰,由图中计算结果看出解析法相对于有限元法在齿边缘的聚磁效应要稍微弱一些,但总体而言两计算结果相差极小证明本全局解析算法是准确的、有效的。
2.2 空载感应电动势的计算
利用全局解析算法对不同时刻空载磁场进行计算即可获得磁链,因此空载电动势的求解可由微分磁链法求得。任意时刻齿中磁通的大小可通过在一个齿距范围内对气隙磁密积分求得。故A相定子齿的磁通φA为

(13)
式中,l为铁心轴向长度,x1、x2为转子某一位置时A相齿两边所处的圆周方向坐标。
设每齿上集中绕制的线圈匝数WA,A相线圈的磁链ψA为
ψA=WAφA
(14)
A相的感应电动势为
(15)
解析法与有限元法的空载感应电动势计算结果波形对比如图5所示。

图5 空载感应电动势解析波形和有限元波形比较
图中有限元法计算结果的幅值为187.12 V解析法计算结果幅值为181.93 V,由于解析法计算的电机槽型做了简化处理而有限元计算的模型是电机的实际模型所以两计算结果会有略微的差异,在误差允许的范围内两波形基本吻合,验证了本解析算法对电机模型的适用性。
2.3 齿槽转矩的计算
本文中齿槽转矩解析表达式的推导是基于麦克斯韦应力张量法。结合解析解可得齿槽转矩的表达式为
(16)
分别利用全局解析算法和有限元算法对电机齿槽转矩的一个周期进行计算比较如图6所示。

图6 齿槽转矩解析波形和有限元波形比较
由图6可看出计算模型的差异使得两种算法的结果有微小差别但波形基本相同同样验证了本解析算法的有效性和准确性。
2.4 空载感应线电势的实验验证
实验样机为功率5 KW,额定电压400 V,转速100 r/min的20极72槽外转子永磁风力发电机,实验平台如图7所示,样机实物如图8所示,在额定工作状态下对该样机的空载感应线电势进行了测量结果如图9所示。

图7 实验平台

图8 实验样机

图9 感应电动势有效值
根据图9测量仪器显示此时样机空载感应线电势有效值为259 V,峰值为366.4 V。采用解析算法求得样机感应电动势的有效值约为249 V左右峰值为353 V左右,由于受实验环境、测量仪器等现实因素的影响实测结果与解析计算结果在允许范围内仅存在微小差距,从而验证了全局解析算法的正确性。
3 基于全局解析-模拟退火算法的优化设计
3.1 模拟退火算法
模拟退火算法是一种全局寻优算法其原理来源于固体的物理退火过程,首先将固体温度加热到充分高再让其缓慢降温。在加温的过程中由于固体内能增加其内部粒子变为无序状态,随着温度的递减固体的内能减少其内部粒子逐渐趋向于有序的状态当固体内能减到最小时达到平衡状态。该算法具有以一定的递减式概率接受恶化解且对目标函数要求少等特点,同时具有鲁棒性强、使用范围广、求得最优解的可靠性高、算法简单等优点。由于算法采用特殊的寻优方法因此在寻优过程克服了易陷入局部最优解的缺点[19]。
3.2 齿槽转矩的优化实现
样机模型在解析算法的基础上得到齿槽转矩解析表达式,以齿槽转矩的幅值作为目标函数,以解析模型的极弧系数、定子槽口宽度、永磁体厚度、气隙长度这几个对电机齿槽转矩影响比较大的参数作为优化变量,在保持其他变量不变的情况下,采用全局解析-模拟退火算法对目标函数进行优化。全局解析-模拟退火算法流程如图10所示。

图10 全局解析-模拟退火算法流程图
3.3 仿真实验验证
在全局解析模型的基础上利用全局解析-模拟退火算法对电机的齿槽转矩进行优化,各优化变量取值范围如表2所示。

表2 各优化变量取值范围
设定解析-模拟退火算法中初始温度为100度,马尔可夫链长度为200、温度衰减函数为指数函数。目标函数的优化过程和适应度进化曲线分别如图11和图12所示。

图11 目标函数的优化过程

图12 适应度进化曲线
优化结果显示解析模型的定子槽口宽度、极弧系数、定子铁心外径、永磁体外径分别为2.18 mm、0.934、223.02 mm、232.36 mm时目标函数取得最优值为0.373305即为电机齿槽转矩的幅值。
4 外转子永磁风力发电机优化结果分析
为进一步验证本文所提出优化算法的正确性,结合之前的分析当槽口宽度、极弧系数、定子铁心外径、永磁体外径分别为2.18 mm、0.934、223.02 mm、232.36 mm时齿槽转矩取得最小值,在此参数下对电机的齿槽转矩、径向气隙磁密、感应电动势、径向气隙磁密谐波进行了计算分析并将结果与优化之前进行比较如图13~图17所示。
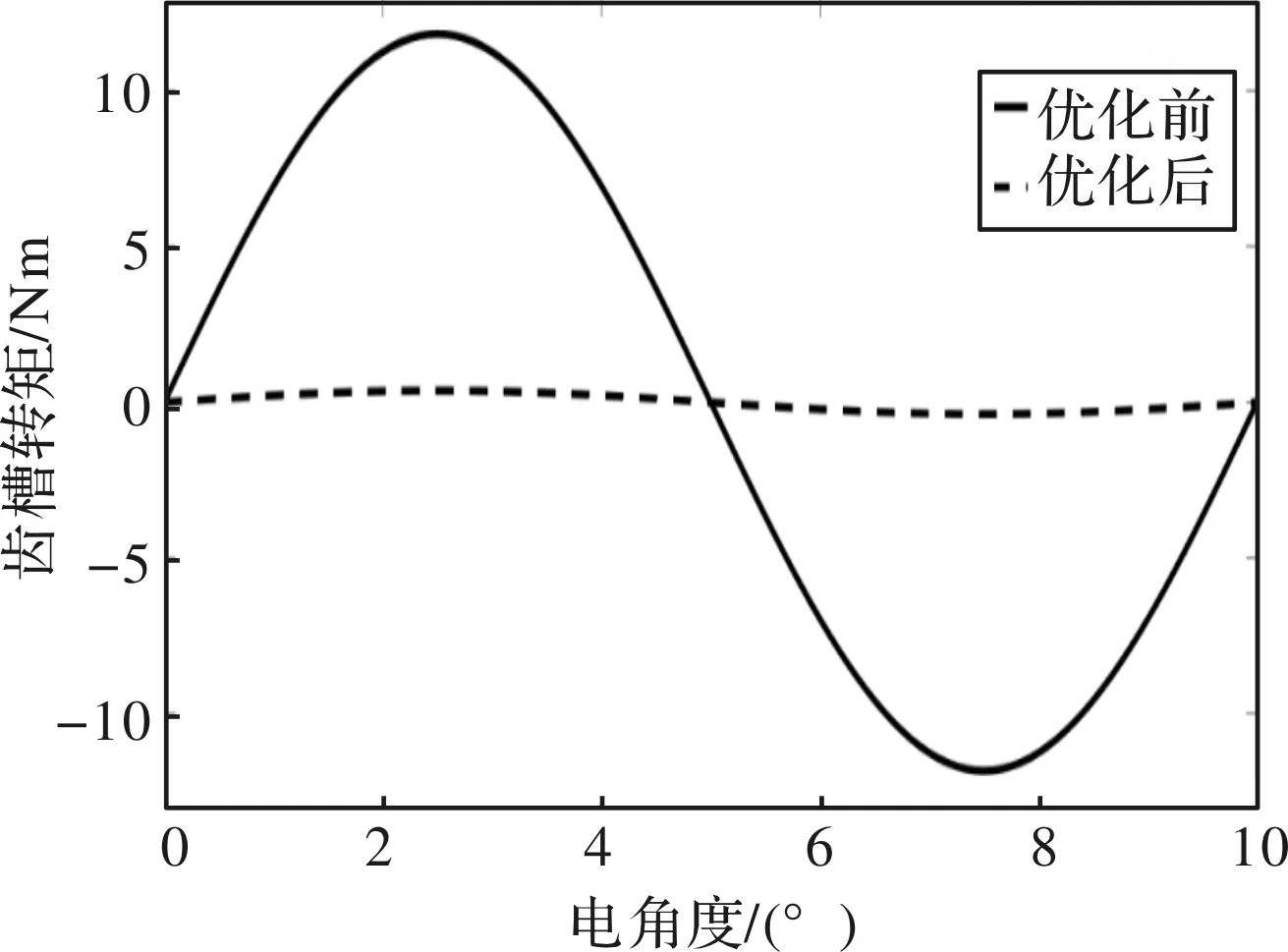
图13 电机优化前后齿槽转矩波形比较

图14 电机优化前后气隙磁密波形比较

图15 电机优化前后感应电动势波形比较

图16 电机优化前径向气隙磁密分量谐波分析
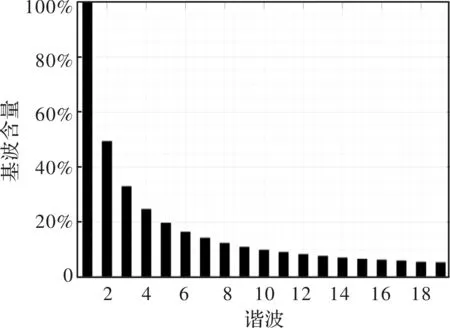
图17 电机优化后径向气隙磁密分量谐波分析
分析各仿真实验结果可以看出通过减小槽口宽度,增大极弧系数,增大永磁体外径Rr即增大永磁体厚度,增大定子铁心外径Rs即减小气隙长度几种措施配合可以有效改善电机性能使得电机的齿槽转矩幅值由11.342 N减小到了0.373305 N,感应电动势幅值由181.93 V增加到了186.72 V且气隙磁密切向分量中对齿槽转矩影响较大的18次谐波由之前的5.68%下降到了4.51%。以上仿真实验结果充分说明了本文所提出的全局解析-模拟退火算法的正确性和有效性,电机优化前后各参数对比如表3所示。

表3 电机各参数优化前后对比
5 结 论
本文利用全局解析算法建立了一台表贴式外转子永磁风力发电机的解析模型,首先通过仿真计算和实验测量证明了所建立解析模型的准确性,然后以齿槽转矩的幅值为目标函数利用全局解析-模拟退火算法对电机齿槽转矩进行优化设计并得到以下结论:
(1)全局解析算法与传统的半解析算法相比运算结果更精确且磁场建模更方便,与有限元算法相比省去了网格剖分等复杂过程,减少了人为干扰等因素,从而使得电机磁场参数等计算更加快速、简捷、准确。
(2)对一台额定功率为5 kW,额定电压400 V,转速100 r/min的20极72槽外转子永磁风力发电机的表贴式外转子永磁风力发电机空载感应电动势进行实验测试,将仿真和实测结果与解析计算结果对比证明了所提出全局解析算法的准确性和适用性。
(3)传统的电磁场分析方法如有限元分析法、图解法等不可联合现代智能优化算法对电机进行优化设计,而利用解析算法可以联合智能算法对电机齿槽转矩进行优化设计。
(4)运用本文新提出的全局解析-模拟退火算法对电机进行优化设计能有效克服其他算法所带来的全局搜索能力差、易陷入局部最优解、运算速度慢等缺点。优化结果显示电机的齿槽转矩幅值由11.342 N降低到了0.373305 N,证明了所提出算法的有效性。

