一种在线数据驱动的永磁直线电机优化设计

尹绍杰，林 鹏，杨扬戬，朱优优，王 威

(浙江大学台州研究院，浙江 台州 318000)

0 引 言

永磁直线电机是一个强耦合的非线性系统，很难建立精确的解析模型进行分析和优化设计。一般地，有限元分析是将复杂的求解域问题化解为多个互联的子域问题，通过用迭代的方法求得每个子域问题的近似解，然后推导出整个求解域上总的满足结构平衡条件的解。有限元分析在复杂的高非线性计算问题中具有计算精度高的优点，被广泛用于电机的分析和优化设计[1]。

在文献[2]中，利用有限元法对永磁无刷直流电机进行参数扫描分析，选出合适的槽极配合、极弧系数和定子槽口宽度，电机齿槽转矩得到大大削弱。虽然有限元分析精度虽高，但耗时长且计算成本高。为此，在文献[3-4]中，运用限元法与田口法相结合的方法，对优化的设计参数建立正交表并进行有限元仿真，最终从正交表中确定最终方案。该方法大大减少了有限元仿真次数，与参数扫描法相比其优化效率得到提高，但缺点是离散型优化且仅适用于单目标优化。在文献[5]中，采用响应面模型与遗传算法相结合的优化方法，对永磁同步电机的齿槽转矩建立响应面模型并优化，优化结果与有限元结果对比均能达到优化指标，且前者优化效率更高。在文献[6]中，一种基于kriging模型结合高效全局优化算法(EGO)的优化方法用于直线感应电机的多目标优化设计，以较少的计算成本得到全局最优解，实现电机牵引力大、能效水平高、重量轻且体积小的目标。文献[7-8]中，采用一种代理模型、优化算法、六西格玛的稳健设计方法，对永磁电机进行系统级的优化设计，保证了电机从设计到制造全过程的高效输出。综合来说，文献[5-8]都是离线数据驱动的优化设计，其优化过程十分依赖原始样本的数量和质量，其直接影响代理模型的精度和优化效果的好坏。在文献[9]中，一种基于期望提高和K均值聚类的加点策略，有效提高了代理模型精度，减小了计算成本。

为解决离线数据驱动优化的不足，本文提出一种在线数据驱动的永磁直线电机优化设计方法[10]。该法采用kriging模型构建目标函数模型，期望提高和K均值聚类用于优化过程中选出模型预测差的未知点，并借助matlab与ansys maxwell联合仿真实现在线加点，提高kriging模型精度。通过多目标粒子群算法迭代寻优，实现永磁直线电机低推力波动和高平均推力。

1 数据驱动优化的原理

根据优化过程中是否产生新样本数据，可将优化分为离线数据驱动优化和在线数据驱动优化两类。

1.1 离线数据驱动优化

对于离线数据驱动优化，优化过程中无法产生新的样本数据，这就表示离线数据驱动优化主要是基于初始样本建立的代理模型进行空间寻优，如图1所示。

图1 离线数据驱动优化

初始样本：电机在优化前需要一定数量的初始样本，样本数据越多、分布越均匀，电机模型拟合精度越高。均匀的初始样本可通过试验设计获得，常用的试验设计方法有全因子试验设计、正交试验设计、拉丁超立方试验设计等。

代理模型：电机内部存在电磁耦合场，很难求得其数学解析模型，利用样本点来拟合出电机代理模型，一方面解决了数学解析模型的问题，另一方面代替了有限元计算，大大缩短了计算时间，提高了计算效率。常用的代理模型有多项式模型、径向基模型、kriging模型、支持向量机回归模型等。

迭代寻优：代理模型建立后，辅助优化算法可以对设计空间进行快速迭代寻优，最终获得电机目标函数的最优解。常用的优化算法有模拟退火算法、差分进化算法、遗传算法和粒子群算法等。

离线数据驱动优化结构十分简单，但优化效果的好坏直接取决于代理模型的精度高低，而代理模型又非常依赖初始样本的数量和质量。显然，过多的初始样本会大大增加有限元计算时间，且初始样本数量过多试验设计很难满足均匀性。针对此问题，下面提出了一种在线数据驱动优化方法。

1.2 在线数据驱动优化

与离线数据驱动优化相比，在线数据驱动优化表现更加灵活。图2显示，期望提高的在线加点策略使代理模型与迭代寻优构成局域闭环，这为改善代理模型提供了更多机会，充分发挥了优化算法性能。此外，在线数据驱动优化需要的初始样本数据少，便于试验设计满足均匀性。

图2 在线数据驱动优化

值得注意的是，离线数据驱动优化可以看成是在线数据驱动优化的特例，因为在开始优化之前，都需要一定数量的样本来拟合代理模型。不同之处在于离线数据驱动优化为单链式结构，上一环节的质量直接决定下一环节结果的好坏。而在线数据驱动优化对初始样本数量要求较少，样本分布均匀且冗余度低，提高了样本利用率的同时减小了计算成本。虽然会带来代理模型精度不高的问题，但通过模型期望提高为目标函数的迭代寻优，将预测误差大的预测点作为新的样本点加入至原样本集，并更新代理模型。经过几次迭代，代理模型将以最小的样本数量获得模型高精度预测，缩短了计算成本。

2 在线数据驱动优化的设计

在线数据驱动优化的设计主要包括试验设计产生初始样本、构建代理模型、在线加点策略设计、优化算法的选择和设置四个部分。文中分别采用拉丁超立方试验设计获取初始样本，kriging模型构建代理模型，基于期望提高(expected improved，EI)的加点策略进行在线加点以及选择粒子群优化算法进行迭代寻优，具体的优化流程图如图3所示。

图3 在线数据驱动优化流程图

2.1 试验设计

试验设计是一种对设计空间中不同样本点位置的排列设计。试验设计是构建代理模型的基础，目标是实现分布均匀的样本空间。文中采用的拉丁超立方试验设计，其原理是n维空间抽m个样本，将每一维分成m个区间，每个区间只取样一次，随机组合。拉丁超立方试验设计是一种分层抽样设计[11]，对设计参数的数目和样本数没有限制，操作容易，优于全因子试验设计和正交试验设计。

拉丁超立方试验设计的随机组合在创造多样性结果的同时也带来了表现的不稳定性。为了克服其缺点，一种基于最大最小距离准则的改进拉丁超立方试验设计在文中被采用[12]，目的是使点与点之间的距离尽可能地最大，保证了输出样本的稳定性。

2.2 Kriging模型和期望提高

Kriging模型是一种利用已知样本点和样本空间位置信息，来求得未知点无偏估计和估计方差最小的插值技术。Kriging模型由回归部分和随机部分这两部分构成，其表达形式为

y(x)=F(β,x)+z(x)

(1)

F(β,x)为回归部分，提供模型全局的预测，是由p个函数的线性组合来获得未知点的大体估计，即

F(β,x)=β1f1(x)+β2f2(x)+…+βpfp(x)

(2)

其中,p有三种形式：常数型，p=1；线性型，p=n+1；二次型，p=(n+1)(n+2)/2(n为x的维数)，β为系数。z(x)为随机部分，在模型回归预测的基础上进行局部的无偏估计，满足

(3)

其中,R(θ,xi,xj)是的关于参数θ的相关函数，常采用Gauss函数，具体形式为

(4)

可以看出，kriging模型的随机部分z(x)服从期望为0、方差为σ2的正态分布。

(5)

其中，β*=(FTR-1F)-1FTR-1Y，γ*=R-1(Y-Fβ*),Y为样本的函数值，r与R形式类似，表示的是未知点与已知样本点的空间位置关系。给出预测值的同时提供预测误差，这就是kriging模型与其它模型最大区别之处。

(6)

2.3 K均值聚类在线加点

对于未知点的预测，其EI值越大，则在该点处模型的预测误差越大。为了改善kriging模型的预测精度，将EI值大的预测点计算得到真实值，加入至原样本集并更新kriging模型。然而实际操作中可发现，kriging模型是一种利用未知点周围已知样本点来估计的插值技术，当kriging模型对某一小块区域预测精度差时，该区域的未知点都具有近似的EI值。倘若每个点都要计算获得真实值，计算量将会大大增加。为此，如图4所示，文中采用K均值聚类的方法，从预测精度差的区域中选出具有代表性的点，在线计算真实值后加入至原样本集并更新kriging模型，提高模型精度的同时减少计算量。

图4 K均值聚类在线加点

3 永磁直线电机的多目标优化

文中以一台12槽10极永磁直线电机为例，采用在线数据驱动优化对永磁直线电机进行优化设计。永磁直线电机的拓扑结构如图5所示，初级为短动子，由电枢铁心和三相绕组组成；次级是长定子，由N、S极永磁体和铁轭组成。永磁直线电机的结构参数和材料如表1所示。

图5 12槽10极永磁直线电机

表1 永磁直线电机的结构参数和材料

对于永磁直线的多目标优化，其设计参数有6个，分别为槽口宽度bs0，槽宽bs1，永磁体宽度wpm，永磁体高度hpm，辅助极高度h和距离d，如图6所示。而优化的目标是减小永磁直线电机的推力波动，提高永磁直线电机输出的平均推力。

图6 设计参数

优化的第一步，对6个设计参数进行试验设计，获取初始样本。如上所述，文中采用基于最大最小距离准则的改进拉丁超立方试验设计，具体操作是通过Matlab的Lhsdesign函数来实现，6个设计参数的范围为

(7)

最终获得初始样本为80，将每个样本的设计参数建立有限元模型，有限元分析后获得目标值推力波动和平均推力。

第二步是建立关于设计参数与目标的代理模型。在构建代理模型之前，将目标进行标幺化处理

(8)

其中，Fpk2pk0为初始推力波动，Favg0为初始平均推力。Kriging模型的具体过程可通过Matlab的Dace工具箱来实现，回归模型采用二次型，相关函数采用Gauss函数，模型无具体的表达式。

代理模型建立后，第三步是采用多目标粒子群算法，最大化两个模型的EI值为目标，进行算法的第一次迭代寻优，目的是寻找出EI值大的预测点，即预测误差大的点，利用K均值聚类法选出具有代表性的预测点，将其有限元计算后加入原样本集并更新kriging模型。然而，粒子群优化算法是在Matlab中运行，有限元计算是利用Ansys Maxwell软件，两者的数据接口不同。为了打破两者壁垒，实现自动调用Ansys Maxwell软件计算及在线加点，文中采用Matlab与Ansys Maxwell联合仿真方法[14]，两个软件之间通过VB脚本文件进行数据交换互通，如图7所示。迭代寻优产生的期望提高加点，其6个设计参数值写入VB脚本文件，执行VB脚本文件调用Ansys Maxwell软件建立有限元模型，且自动运行计算得到目标值平均推力和推力波动，计算结束后软件会自动把目标值录入VB脚本文件，此时Matlab读取目标值并将该作为新样本加入原样本集，最后更新Kriging模型。

图7 Matlab与Maxwell联合仿真

通过期望提高的在线加点，样本数量由初始的80增加至116，模型精度由76%提升至99.7%。若采用离线数据驱动的优化方法，初始样本需290个样本点才能获得99.7%的模型精度。与之相比，在线数据驱动的优化方法缩短了60%的计算周期，整个优化流程效率得到大幅度提高。

当Kriging模型精度足够高时，EI值也满足低于阈值0.05的要求，优化算法进入第二次迭代寻优。此时，优化的变量不变，优化的目标改为提高永磁直线电机的平均推力，降低其推力波动。将平均推力取负值，优化问题变为最小化问题。经历300次迭代，优化基本趋于稳定，两目标函数的Pareto前沿如图8所示。

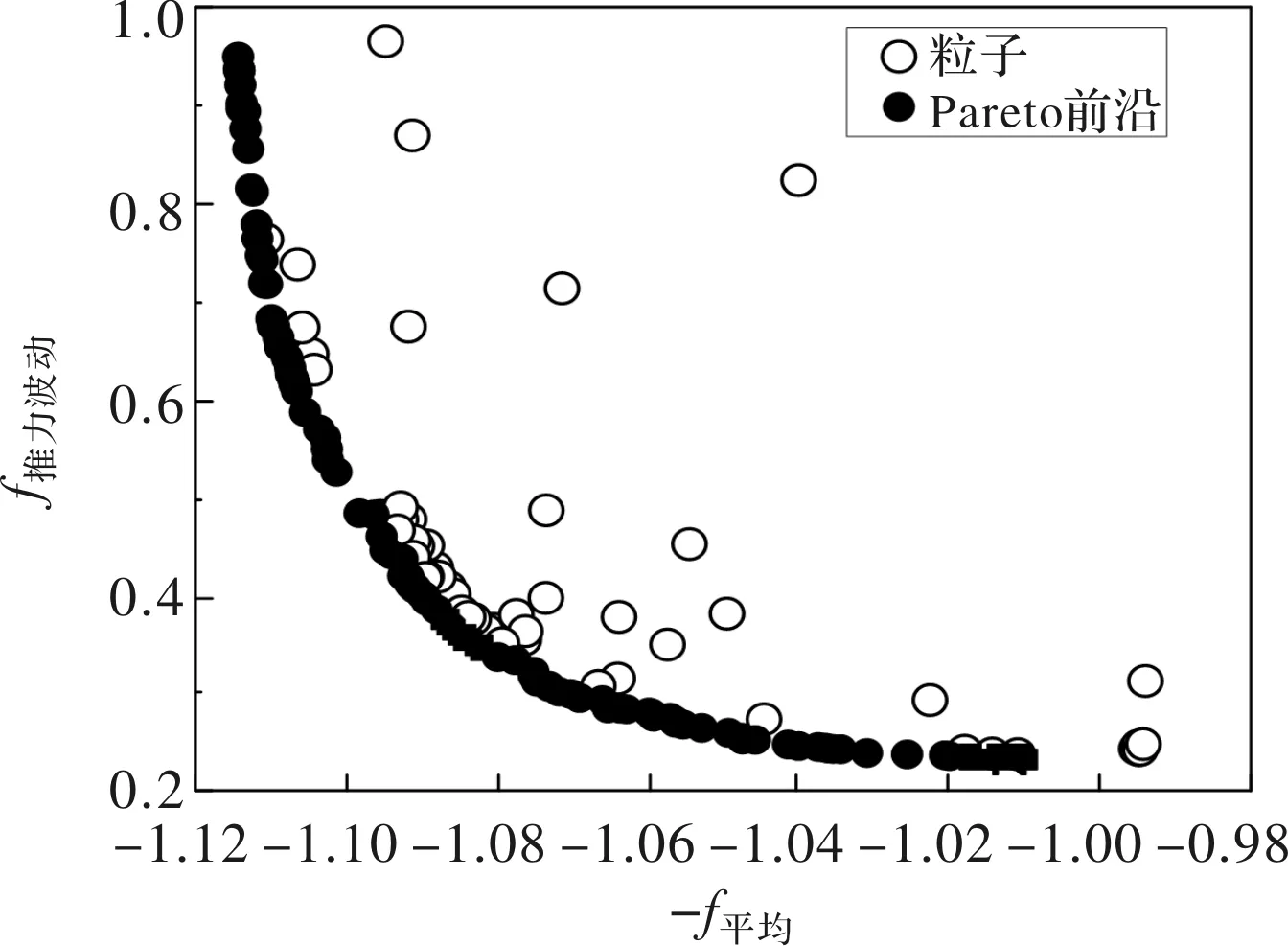
图8 K均值聚类在线加点

两目标函数赋予同样的权重，对Pareto前沿的非支配解作如式(9)处理，值大的被选为最终优化结果

f=0.5(1-f推力波动)+0.5f平均推力

(9)

最终点(f推力波动,f平均推力)为(0.36, 1.066)这组解被确定为优化结果，6个设计参数的优化结果如表2所示。在线数据驱动优化后的永磁直线电机，其推力波动从100 N减少至36N，降低了64%。而其平均推力从627 N增加至668.7 N，提高了6.6%，如图9所示。进一步分析可以看出，初始的永磁直线电机谐波次数多且幅值大，主要是2、4、6次谐波，斜极技术很难全部消除。而优化的永磁直线电机主要是6次谐波且幅值较小，配合一定的斜极可以完全被消除。两者分析对比，验证了优化的有效性。

表2 设计参数优化结果

图9 永磁直线电机优化前后的推力曲线

4 结 论

本文提出了一种在线数据驱动的永磁直线电机优化设计方法。该法采用拉丁超立方的试验设计获得初始样本，利用kriging代理模型建立永磁直线电机推力波动和平均推力两目标的函数模型，附加期望提高和K均值聚类的在线加点策略，结合多目标粒子群优化算法，实现了永磁直线电机推力特性的优化设计。

与离线数据驱动优化设计方法相比，在线数据驱动优化设计方法降低了试验设计难度，提高了样本利用率，保证了代理模型精度，减小了计算周期。该优化设计方法使永磁直线电机获得64%的推力波动减小和6.6%的平均推力提升，且适用于其它优化问题，具有一定的参考价值。