浅析类比思想在数学教学中的应用
筅江苏省江阴高新区实验中学 陈丹洁
1 引言
数学是一门海纳百川的基础学科,我们虽不奢求能理解与掌握其所有的知识,但我们可在自身已有认知的基础上,将一些陌生的问题转化成我们所熟悉的内容,类比思想则是实现这一转化常用的一种方法[1].
类比思想是指根据两个或两类具有相似性质的事物推断出它们可能存在的其他类似之处的思想,因有明确的对比分析的对象,因而可省略大量研究所需耗费的成本[1].它在数学领域中对联系新知识和旧知识具有桥梁的作用,又对猜想的形成起到较好的推动作用.
2 运算类比,理清算理
运算能力不仅是一种重要的数学能力,还对物理、化学等学科的学习有着直接的影响.运算过程体现了学生的逻辑思维过程,在运算中运用类比,能将算理的本质暴露于学生的思维中,让学生更加快速、简便地掌握运算方法,提高运算效率,达到灵活应用的程度.
案例1:“有理数除法运算”的教学.
课前,笔者展示一个式子:(-4)×(-2)=8.
师:根据运算法则,我们可以将此式发生怎样的变化?
生1:根据运算法则,可将乘法转化为除法,即8÷(-4)=-2.
师:很好,这就是将有理数的乘法转化为除法的过程,8÷(-4)=-2这个式子中,8为被除数,-4为除数,根据我们以往学过的运算规则,该怎么将除法运算转变为乘法运算?

有理数的除法规则通过类比的方式昭然揭晓,学生在类比中也欣然接受了有理数除法运算的这种本质特征.为了巩固与检验学生对这个算理的理解与掌握程度,教师可设计一些常规题供学生练习.
以类比思想帮助学生掌握运算规则的过程,不仅仅是让学生掌握一种运算方法,更重要的是教会学生解决一类题的思想方法,这种数学思想的形成对数学学习具有重要的促进作用.因此,类比思想在运算中的应用值得每个师生重点关注.有效地掌握这种方法,可以让学习变得轻松,在提高学生运算能力的同时,帮助学生获得良好的数学思维能力.
3 概念类比,启发思维
概念或定理等是数学的基础,每个概念并非是独立存在的知识点,它们之间有一定的内在联系[2].教学中,我们可充分利用这种联系,通过类比的方式帮助学生弄清每个概念和定理的性质.一旦理清了各自的性质,就能很好地联系新知与旧知.因此,类比过程又是联系新知与旧知的桥梁.
案例2:“相交线与平行线”的教学.
为了让学生从根本上理解相交线的性质,笔者采用了实践操作与小组合作学习相结合的方式进行教学引导.引导过程中,笔者添加了类比的教学手段,以帮助学生明晰相交线所涉及的定理为形成与发展解题能力奠定基础.具体如下:
师:如图1,在a,b两根木条的中间钉一颗钉子,让这两根木条能围绕这颗钉子自由转动.

图1
学生操作.
师:现在请各组将自己所完成的作品,抽象成平面图形,并思考所形成的图形中会出现几个小于180°的角.
生1:如图2,根据实际情况,我们组画出了四个小于180°的角,分别用∠1、∠2、∠3与∠4表示.

图2
师:很好!如果我们将这四个角进行任意组对,能组几对?
生2:根据之前学过的排序规律,四个角可以组成3+2+1=6(种)组合.
师:现在请各组分别将这6种组合写出来,并根据每一对的位置关系进行分类,看看能分成几类,并说明理由.
组1:相邻的角分别有:∠1、∠2,∠2、∠3,∠3、∠4,∠4、∠1,共4组.
组2:相对的角分别有:∠1、∠3,∠2、∠4,共2组.
组3:具有公共边的角分别有:∠1、∠2,∠2、∠3,∠3、∠4,∠4、∠1,共4组.
组4:没有公共边的角分别有:∠1、∠3,∠2、∠4,共2组.
师:非常好!从刚刚大家的分析看,角相邻,且一条边为公共边,另一条边互为反向延长线的角的度数和是180°,分别有∠1、∠2,∠2、∠3,∠3、∠4,∠4、∠1,共4组,我们称这类角互为邻补角;而角的位置相对,且两条边都互为反向延长线的分别有:∠1、∠3,∠2、∠4,共2组,此类角我们称为对顶角.从以上环节看,邻补角和对顶角分别需要具备怎样的条件?
生3:首先要有两条直线相交的条件.
生4:在两直线相交的条件下,有一个公共顶点,但是没有公共边的两个角互为对顶角;有一个公共的顶点和一条公共边的两个角互为邻补角.
师:太棒了!我听到你们用了“互为”这个词,为什么?
生5:只有在谈论两个角之间的关系时,才称得上互为.如图2,∠2、∠4互为对顶角,而∠3、∠4则互为邻补角.
本片段中,教师引导学生自主实践、探索、观察、发现角与角之间的位置关系,根据不同的分类方法获得不同的数学定理.这种方式不仅让学生亲身经历、体验了邻补角与对顶角概念的形成过程,还让学生在邻补角与对顶角的对比中明晰了各自的本质.这种方式不仅训练了学生合作交流的能力,还有效地渗透了数学中常用的分类讨论思想,培养了学生的类比思想.
4 解题类比,迁移能力
数学学习除了要发展学习者的智力水平与个人能力,最直接的表现就是解题能力的培养[3].在以中、高考为晋级制度的今天,应试虽不是最主要的教育目的,却是学生进入高等学府的重要路径,解题能力的高低决定了学生未来受教育的层次.为此,笔者在例题教学中,常运用类比的方式,鼓励学生在已有的认知水平上进行类比分析,以实现知识的正迁移,从而提高各项数学能力.
众所周知,每个知识点衍生而成的试题品种繁多,题型多样,若想用传统的题海战术应付中、高考,简直是痴人说梦,比登天还难.笔者研究了近些年各地的中考试题,发现试题常出常新,每年都会出现新颖的问题.为此,我们唯有教会学生解题方法,通过一道题辐射到与它类似的一类题,在类比中真正地实现知识的迁移,达到触类旁通的教学目的.
案例3:“一元一次方程”的解题教学.
首先与学生一起探讨解一元一次方程遵循的规则或步骤.(1)去分母.对于含有分母的方程,应先在方程的两侧同时乘或除以各个分母的最小公倍数,特别要注意的是,不含分母的项也要同时乘或除以这个数.(2)去括号.与之前所学过的运算规则一样,按照小、中、大括号的顺序分别去除,此过程中,需特别留意括号前是负数的情况,注意符号的变化.(3)移项.尤其注意符号的变化.(4)合并同类项.(5)将未知数的系数化为1.以上为常规解题步骤,但遇到特殊情况的时候,可特殊对待.
原题:解一元一次方程:6+3x=2+5x.
本题比较简单,主要是为了让学生体验解方程的步骤与过程.与以上解题步骤一一对应来看,本方程中不存在分母、括号,因此可省略掉前两个步骤.本题中,等号左、右两边都有未知数,需执行步骤(3),移项为3x-5x=2-6,接下来合并同类项,合并后为:-2x=-4.随后化简系数可得x=2.
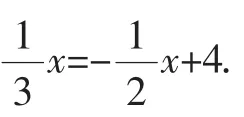
此题与例题相比,难度稍有增加.经创新后的方程,对照解题步骤,五个步骤一个都不能少.学生在与原题的类比中一一对照解题步骤进行解题,笔者在巡查中发现学生解题的正确率很高,只有个别学生在去分母环节中忘记常数项同时乘最小公倍数6,导致错误的发生,其他大部分学生解题过程清晰,结论正确.
总之,采取怎样的教学方法能快速帮助学生突破思维的障碍与知识的重点与难点问题,值得我们每个教师思考与探索.类比思想的运用,对概念、定理、性质、解题等的教学都有良好的促进作用,它对激发学生的探究欲,开启学生的数学思维,建构新知等,都有重要的影响.因此,我们应根据教学实际,选择相应的教学方式,从真正意义上实现“减负增效”的教学效果.

