深刻理解教学内容，精准划分教学单元——以“一元二次方程”教学单元的划分为例

筅江苏省南通市启秀中学 李庾南

筅江苏省南通市教育科学研究院 刘东升

1 引言

自20世纪70年代末，我们提出“自学·议论·引导”教学法以来，围绕初中数学开展单元教学的实践研究一直没有停止．2014年《初中数学“自学·议论·引导”教学35年探索实践》获得首届国家基础教学成果一等奖，在中国教育学会中学数学专业委员会的关心和支持下，已在全国多地开展了四期“自学·议论·引导”教学法研修推广活动，来自全国各地的实验区、实验教师积极投身“自学·议论·引导”教学法的实践研究，特别是开展初中数学单元教学的实践，取得了很多研究成果，丰富了“自学·议论·引导”教学课例的覆盖面．然而，也有少数实验教师对单元教学的单元划分还存在着理解不深的情形，比如，将单元教学课上成“压缩饼干”课“走马观花”课，影响了课堂教学品质的提升．笔者以人教版教材第21章“一元二次方程”为例，从“用教材教”的角度对全章进行单元划分，并给出教学建议，供大家讨论．

2 “一元二次方程”全章学习目标及逻辑结构

2.1 学习目标

（1）了解一元二次方程及相关概念，能熟练地将一元二次方程整理、变形为一般形式ax2+bx+c=0（a，b，c为常数，且a≠0）．

（2）理解直接开平方法、配方法、公式法、因式分解法及其相互联系，并能根据方程的特点灵活选取不同方法解一元二次方程（主要是数字系数的一元二次方程）．

（3）会用一元二次方程根的判别式判定方程是否有实根和两个实根是否相等．

（4）了解一元二次方程的根与系数的关系，并能初步运用．

（5）能根据具体问题中的数量关系列出一元二次方程，并利用一元二次方程模型解决简单的实际问题，能根据具体问题的实际意义，检验方程的解是否合理．

2.2 理清知识的逻辑结构，建构知识结构图

本章的逻辑结构图拟分为两幅研究，分别是一元二次方程的概念及相关概念（见图1）、一元二次方程的解法与建构运用（见图2）．

图1

图2

3 划分“一元二次方程”的“教学单元”

我们根据“先见森林，后见树木”的方式，将“一元二次方程”全章分为四个单元．

第一单元：一元一次方程的定义及相关概念，探求降次求解的路径，初步了解四种方法及相互关系．

例如，可类比一元一次方程的知识，迁移、调整，生成一元二次方程概念（定义，一般式，解的定义）；明确了解一元二次方程的方向，是将原方程有根有据地逐步变形为一元一次方程“x=a”后，给出数学情境，依次研究4个一元二次方程：（1）x2-4=0；（2）x2-2x=0；（3）x2-2x-15=0；（4）ax2+bx+c=0（a≠0）．

探究：用配方法解一般形式的一元二次方程，得到利用系数表示根的公式（公式法）．

目的：建立解一元一次方程的基本思想、具体方法和理论依据的知识体系框架，激发自主探索学习的意识、兴趣，培养自我获取、构建、发展、超越的精神和能力．

第二单元：理解一元二次方程四种解法的理论依据和操作时的注意点，正确、灵活地选用适当的方法解一元二次方程．

重点、难点：用配方法解一元二次方程．

可渗透运用配方法将二次三项式恒等变形为a（x+m）2+n的形式，有利于以后研究二次函数的图象的顶点坐标．

第三单元：一元二次方程根的判别式，根与系数的关系．

从一元二次方程的求根公式出发，引导学生关注根的判别式，并由两根的系数的特点，得出根与系数的关系．本单元的知识结构如图3所示，可作为板书设计．

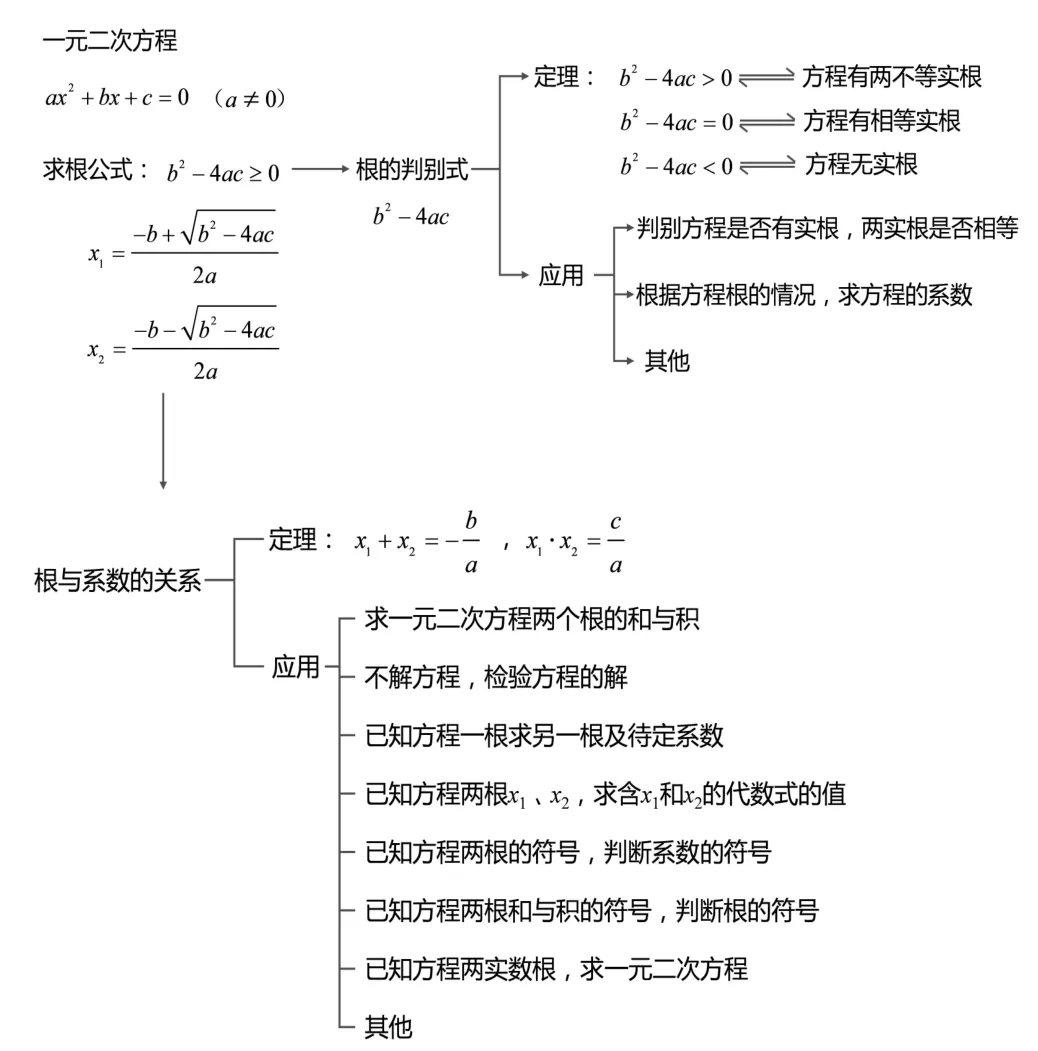
图3

第四单元：一元二次方程与实际问题．

选择典型实际问题，重点引导学生列方程（建模），然后解方程，最后要注意检验方程的解是否符合实际．本单元的知识结构如图4所示．

图4

4 关于划分教学单元的一些建议

4.1 理解教学内容是划分教学单元的前提

深刻理解教学内容，深入研读教材、教参，是精准划分教学内容的前提［1］．上文中以一元二次方程全章的单元划分为例，先理清全章的学习目标、知识结构图，然后划分为四个教学单元．值得一说的是，第一单元从一元二次方程的定义出发，研究了一元二次方程相关概念之后，就用几个具体的一元二次方程得出几种解法，但并没有深入研究解法及其之间的关系，也没有将配方法“推向一般”，这样的教学单元划分的依据是“先见森林，再见树木”，为第二单元全面研究一元二次方程的解法提供了必要的“数学情境”（学生已知道了一些不同的“降次”解法）．第三单元主题关注一元二次方程根的判别式，就选择从上一单元积累下来的“求根公式”出发，研究“根的判别式”并定义符号Δ，然后研究根与系数的关系．这个单元的内容比较重要，带领学生学深悟透之后，有利于将来从二次函数视角继续认识它们的价值．

4.2 理解班情学情是确定单元课时的关键

基于教学内容划分教学单元之后，需要结合班情学情确定每个教学单元内的课时数．还以一元二次方程为例，第一教学单元是研究一元二次方程的定义、相关概念，对于解法，只是初步接触并不是全面系统研究，所以这个教学单元只需1个课时即可，不必增加习题课，如果增设习题课，就会出现一元二次方程的解法习题，而解法训练是第二单元的学习目标．到了第二教学单元，则需要结合学情相机确定教学课时，如果班级学情较好，则安排1节习题课（训练学生一元二次方程的解法），如果班级学情一般，则需要2~3节习题课组织学生训练解法，达到解答正确、熟练、快速的教学目标．第三教学单元“根的判别式”“根与系数关系”也需要2～3节习题课，因为有一些含参的方程问题值得训练和讲评．在第四教学单元带领研究实际问题与一元二次方程，重点是分析等量关系，构建数学模型(一元二次方程)，然后求出方程的解，并回代入实际问题检验．在这个教学单元中，如果班情学情较好，则理解和分析等量关系可能会顺畅一点，需要2个课时左右即可，如果学生对实际问题的理解不快，则可能要增加2个课时进行变式再练．

4.3 划分教学单元后需要精心选编例习题

基于“学材再建构”划分教学单元之后，常常与教材上的内容(知识和习题)呈现的顺序不同，这也是从“照本宣科”走向“用教材教”的专业追求．我们认为，针对划分教学单元的内容和教学重点与难点，由于每个教学单元的第1课时侧重的是知识探究与生成[2]，所以例题、习题的教学时间相对较少，有时甚至没有安排例例题、习题的教学环节，在后续跟进的习题课中，教师要精心选编例、习题进行训练．以上文中提到的一元二次方程的第三个教学单元为例，一元二次方程的根的判别式、根与系数关系的习题训练非常关键，而教材上这方面的习题量并不充足，需要教师改编和原创，有时甚至要到二次函数的图象与坐标轴公共点的综合题中寻找相应题源进行改编，以便让学生对根的判别式、根与系数关系的相关习题达到较为熟练的运算或变形能力，为日后学习或理解函数问题储备必要的运算技能．此外，关于选编例题、习题的另一个建议是，要尽可能让“习题”走向“问题”，一节课中使用20道左右习题的“导学案”其实是习题汇编，并不是教学设计，好的教学设计中的一节课的题组最多4个，每个题组下面可以预设3～6个系列问题，带领学生把这个题组学深、学透．可见，在开展单元教学的习题课教学设计时，对教师命题基本功也提出了较高的要求．

W