发展学科素养，驾驭课堂教学——以一次函数的教学为例

筅山东省东营市垦利区永安中学 周锡花

1 引言

教育部提出当代课堂教学需要帮助学生建构学科核心素养.那么，在初中数学课堂教学中，如何帮助学生建构学科核心素养？笔者认为，还是重在“育人”上.以一次函数的教学为例，其数学核心素养包括理解一次函数的概念、认知函数的图象，在这些相关信息获取的过程中，帮助学生建构数形结合思想，发展逻辑思维能力；同时在解决实际问题的过程中，使学生初步认识一次函数与人类生活是密不可分的，进一步发展学生释疑、解疑的能力，从而驱动学生探究数学学科素养的潜能［1］.

2 解读课堂教学中数学核心素养涵盖的内容

数学课程标准指出：“数学核心素养为具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力.”笔者认为，数学教育的终极目标是学生进入社会生活后，能够利用所学的数学知识观察世界、思考世界，并将其结果用数学的语言表达出来.在这个过程中，观察的本质就是抽象的数学特性，思考的本质就是推理思维的严谨性，而数学语言则是建模化的数学运用.

以一次函数的课堂教学为例.其数学核心素养确定为数学概念认知、一次函数的关系式与图象间的逻辑推理、函数图象的建模、思维的直观想象、函数的相关数学运算、图象与函数式的数据分析六方面.这些学科素养需要由简入繁，例如，教学时可以以一次函数y=x作为起点，思考y=2x，再思考y=x+1……让学生观察自己绘出的图象，总结其规律.

通过递进探究的方法，学生得到的启示是一次函数概念的抽象主要表现为函数式与图象中的特征意识和数感，数学转换过程中的逻辑推理能力，函数图象中的模型思想.当然，在探究过程中还有两个超出数学范畴的素养，即学生需要具备的应用意识和创新意识，如图1中，通过y=x在原点的旋转得到y=2x；在图2中，通过y=x向上平移可以得到y=x+1.这样的数学探究活动可以让学生在认知数学概念的同时感悟数学本质，在拓展数学思维的同时建构和发展数学核心素养.

图1

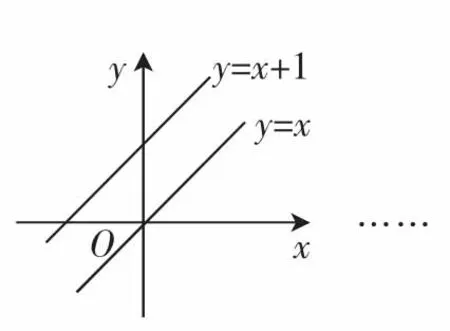
图2

3 落实课堂教学中数学核心素养建构的过程

核心素养是学科的灵魂，怎样才能将数学核心素养的建构落实在初中数学教学中？利用教学实践，笔者有以下几个方面的思考.

3.1 让学生通过学习学会从数学的角度思考问题

我们知道数学涵盖特征意识、数感，在一次函数内容中还有几何直观和空间想象，都属于数学概念抽象性素养的范畴.例如，在学生最初接触一次函数时，对一次函数的认知需要理解自变量和因变量两个较为抽象的概念，学生不易区分，于是创设问题情境：

某学生去联通公司办理手机业务，联通公司提供两种通话计费方式可选：第一种方式是每分钟通话费0.08元；第二种方式是月租费20元，另外每分钟通话费0.05元.请问：无论选择哪种计费方式，费用一样时通话时长为多少？请分析该学生如何选择计费方式才能节省费用.

让学生由问题情境建立费用y元与时间x分钟的关系式，通过函数关系式概括出自变量和因变量的数学概念.在课堂教学中，从某学生去联通公司办理手机业务的具体背景中得出一般规律和建模，并且用数学的概念形式进行表征，这就是一种从数学的角度思考问题的方法.

当然，初中阶段通过建立变量的关系式可以得到抽象的数学概念，包括变量间的关系和法则.让学生在课堂上达成的思考方法是找到变量间的关系特征和变量的意义两个方面.例如，在上述问题情境中得出的变量间的关系是y=0.08x，y=20+0.05x，从变量的指数分析是一次函数，这就是认知变量的特征的思维方法；而y是因x的变化而变化的，体现了一次函数中两个变量的内涵，这就是认知变量的意义的思维方法.

3.2 让学生通过学习学会用数学的思维推理

一次函数相关的数学知识的运算和推理都属于逻辑推理.从推理形式看，逻辑推理存在从特殊到一般的推理，是一种归纳、类比形式的推理；还有一种是演绎形式的推理，是从一般到特殊的推理.在教学中培养学生这两种推理能力也属于数学核心素养建构的主要组成部分.学生学习了一次函数的概念，从其图象特征可知是一条直线，正比例函数是一次函数，类推到正比例函数的图象是一条直线.而正比例函数是一种特殊的一次函数，其图象是过原点的一条直线，但一次函数不一定过原点.从特殊到一般的推理过程是一种演绎推理.因此，在初中数学课堂教学过程中培养学生的逻辑推理比演绎推理更为重要.

数学课堂教学中，因为数学概念的抽象性，会出现学生通过听讲或讨论依然不清楚的现象，可以采用举例说明的方法.通过创设出一些生活情境引导学生进行逻辑推理，逐渐帮助他们对数学概念进行思维建模，这就是学会用数学的思维推理，属于数学核心素养的范畴［2］.

3.3 让学生通过学习学会用数学的语言表达

数学思想的认知过程其实就是对数学思维的建模过程.在一次函数知识框架中存在函数式与函数图象的模型思想、坐标数据分析等，这些都是数学语言的表达形式，其数学思维的建模过程就是对函数式与函数图象的认知.在一次函数的教学过程中，对数学思维的建模就是对现实问题情境进行数学化的过程，用代数式或图象等数学语言表达情境问题，是一种利用数学原理与方法构建释疑的过程.换句话说，数学思维的建模是用数学语言表述问题情境而转化为函数式、函数图象的具体方法.函数思想就是一种数形结合的思想，涵盖了函数式和函数图象两个方面.为了在课堂上能够体现数学思想具有思维的建模，笔者以改编过的2020年江苏宿迁中考数学试卷的第8题进行实例说明.

图3

感知问题情境：读题，对图形进行观察、思考、分析，找到关键词“直线”“顺时针旋转90°”，需要解决的问题是“QQ′的最小值”.

数形转换关系：点A（4，0），点B（0，2），故AB=

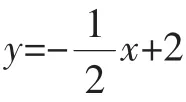
而在现代化建设设计的过程中，数学的真正应用是数学思维的建模，这种建模已经渗透到其他学科的应用中.因此，中考试题体现数学思维的建模是对学生的学科核心素养的检查.

总之，数学核心素养是根据学生的发展特点而产生的，它体现了以生为本的教育理念，涵盖了数学概念具有抽象性，让学生通过学习学会从数学的角度思考问题；数学思维具有逻辑推理性，让学生通过学习学会用数学的思维推理；数学思想具有思维的建模，让学生通过学习学会用数学的语言表达.