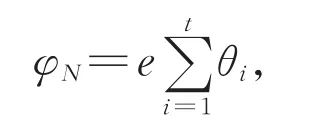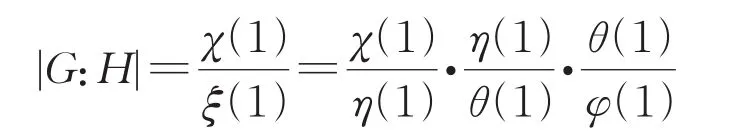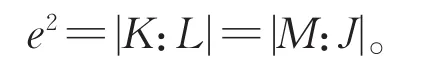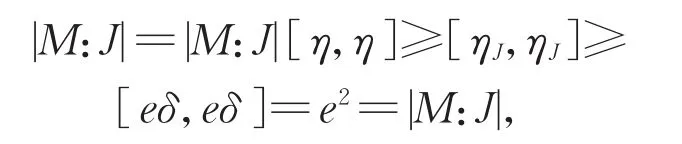关于Berger定理的推广
常慧敏,黄宇敏
(山西大学 数学科学学院,山西 太原 030006)
0 引言
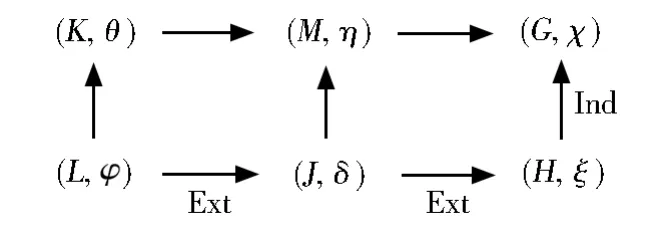
本文涉及的群均是有限群,有关群论和复特征标理论的记号和概念分别来自[1]和[2]。设χ∈Irr(G)为群G的一个不可约复特征标,如果存在真子群H 进而,如果对任意正规子群N⊲G,均有χN=eθ,其 中e为 正 整 数 且θ∈Irr(N),称χ∈Irr(G)是拟本原的,称e为χ关于正规子群N的分歧指数,记为eN(χ)。特征标的本原性和拟本原性是从两个不同的方向(诱导和限制)定义的,直观上看似毫无关联,但实际上二者却有紧密的联系。通过Clifford对应观察得,本原特征标定是拟本原的。但反之不成立,显然非交换单群的不可约特征标均拟本原,但一般不都是本原的,例如交错群A7。事实上,不可约特征标均为本原的群,其结构已经被Hekster[9]给出了描述。著名的Berger定理断言可解群的拟本原特征标均为本原特征标,这是可解群表示理论中很重要的结果,具有广泛的应用。但证明非常艰难,需要借助深刻的射影表示等技术。近年来拟本原特征标的研究取得了很多进展,例如,关于Hall子群上拟本原特征标的扩张问题[10],关于拟本原特征标的零点问题[11],关于拟本原特征标的置换公式问题[12],以及关于拟本原特征标的分解问题[13]。 然而,目前特征标理论中的许多重大猜想,如McKay猜想和Alperin权猜想,在约化为验证单群的证明中,需要不断地“消除”正规子群,通常采用的技术是把所研究的问题“放置”在一个正规子群的上方,通过对该正规子群的指数做归纳,最终归结为拟单群的环境。因此,研究Berger定理的相对版本,即考查某个正规子群上方的不可约特征标的相对本原性和相对拟本原性,是有意义的问题,可为攻克重要的特征标问题提供有力的证明技术。特别地,本文提出的关于一个给定正规子群的相对本原特征标和相对拟本原特征标,均在特征标三元组的同构对应下保持不变,这在应用时非常方便。 下面我们给出特征标的相对本原性和相对拟本原性的概念。 定义1设G为任意群,χ∈Irr(G)且L⊲G。 (1)称χ是关于L的相对拟本原特征标,简称为L-拟本原的,如果对任意的中间正规子群L≤N⊲G,均有χN是齐次的。 (2)称χ是关于L的相对本原特征标,简称为L-本原的,如果不存在中间的真子群L≤H 取L=1即得到通常的拟本原特征标和本原特征标的概念。同样应用Clifford对应可知,L-本原的特征标定是L-拟本原的(证明见本文引理7)。但反之并不成立,那么在何时成立呢?下述结果给出了回答。特别地,取L=1时得到的结论,还是Berger定理的一个加强,并且减弱了原先的可解群条件。 定理1设G是任意群,L⊲G,且χ∈Irr(G)为L-拟本原的。如果G/L为p-可解群,对每个素数p|eL(χ),则χ也是L-本原的。 本文也研究了Berger定理的π-版本,可类似地引入π-部分特征标的相对本原和相对拟本原的概念,具体内容可见第2节。 定理2设G为π-可分群,L⊲G,且φ∈Iπ(G)为L-拟本原。如果G/L为p-可解群,对每个素数p|eL(φ),则φ也是L-本原的。 取π为某个素数的余集,可得到下述Brauer特征标的相应结论,关于该类特征标所涉及的概念和性质具体可参见[14]。 推论1设G为p-可解群,其中p为任意素数,L⊲G,且φ∈IBr(G)为L-拟本原。如果G/L为q-可解群,对每个素数q|eL(φ),则φ也是L-本原的。 在证明本文主要结果时,需要用到下述基本结论,即文献[15]中推论4.2。 本文主要借助Isaacs的π-理论中所给出的π-部分特征标[16],通过对集合π的适当选取,π-部分特征标可对应到复特征标和Brauer特征标,从而达到如此两种经典特征标的统一。 Iπ-特征标的Clifford定理和Clifford对应如下,即文献[16]中推论5.7和定理5.11。 引理3设G是π-可分群,φ∈Iπ(G)。如果N⊲G,则φ在N上的不可约分解为 其中e为正整数,θi∈Iπ(N)两两不同,构成一个G-共轭轨道,并且et整除 |G:N|。进而,如果|G:N|为π'-数,则e=1。 引理4设G是π-可分群,N⊲G且θ∈Iπ(N)。令T=Gθ为θ在G中的惯性群,则通过特征标的诱导在如下两个集合之间可定义一个双射 特 别 地 ,如 果φ∈Iπ(G|θ),则 存 在 唯 一 的μ∈Iπ(T|θ),使得μ既在θ上方又在φ的下方。 假设φ=χ0∈Iπ(G),其中χ∈Irr(G),不可约复特征标χ就称为Iπ-特征标φ的一个提升。显然,对应同一个φ∈Iπ(G),它的提升可以有很多。如何挑选“好”的提升,即具有某种稳定性的提升,这是一个特别值得深入探讨的课题。目前Isaacs 给出了Iπ(G)的一种典范的Bπ-提升,即群G中一类特殊的不可约复特征标集合Bπ(G)通过π-限制χ↦χ0给出了集合Bπ(G)和Iπ(G)之间的一个一一对应。在2∈π时,使用关于群G和素数集合π的一个特定的域自同构得到如下识别Bπ-特征标的办法,即[16]中定理5.2。 引理5设G为π-可分群,2∈π,并且τ为关于G和π的域自同构。如果χ∈Irr(G),则χ∈Bπ(G)当且仅当χτ=χ且χ0∈Iπ(G)。 但当2∉π时,上述关于域自同构的技术失效,不能识别出Bπ-特征标。为了克服这个技术难题,Dade提出了Iπ-特征标一种新的自然的提升。在[17]和[18]中,Isaacs正式命名该种典范提升为Dπ-提升,也就是说通过映射χ↦χ0在集合Dπ(G)和Iπ(G)之间构造了一个一一对应。对任意子群H≤G和θ∈Irr(H),定义θ到G的π-诱 导θπG=(δ(G,H)θ)G,其 中δ(G,H)为π-标准符号特征标。注意到G0中元素均为奇数阶,容易验证 (δ(G,H))0=1。 下面是Dade给出的关于Dπ-特征标的深刻结果,见[18]中定理E。 引理6设G为π-可分群且2∉π,如果H≤G,θ∈Irr(H)和χ∈Irr(G),使 得θπG=χ,那 么θ∈Dπ(H)当且仅当χ∈Dπ(G)。 先证明相对本原性蕴含着相对拟本原性,然后再讨论逆命题何时也成立。为了统一表述复特征标和Brauer特征标中的相对本原性和相对拟本原性,我们考虑该问题的π-部分特征标版本,下述为相关定义(取L=1得到π-部分特征标的本原和拟本原的概念)。 定 义 2设G为π-可 分 群 ,φ∈Iπ(G)且L⊲G。 (1)称φ是关于L的相对拟本原特征标,简称为L-拟本原的,如果对任意的中间正规子群L≤N⊲G,均有φN是齐次的。 (2)称φ是关于L的相对本原特征标,简称为L-本原的,如果不存在中间的真子群L≤H 使用Iπ-特征标的Clifford对应(即引理4)不难证明。 引理 7设G为π-可 分 群 ,φ∈Iπ(G)且L⊲G。如果φ是L-本原的,则φ也是L-拟本原的。 证明任取L≤N⊲G,根据引理3,可令φ在N上的不可约分解为 其中e为正整数,t=|G:Gθ1|。通过Iπ-特征标的Clifford对应知,存在μ∈Iπ(Gθ1)使得φ=μG。因为φ是L-本原的,所以Gθ1=G,从而t=1。因此φN=eθ1,表明φ是L-拟本原的。 因为Iπ-特征标的本原性和拟本原性,通常需要通过提升为复特征标来研究,所以下面我们先考虑一个相对拟本原的复特征标何时也是相对本原的。因为G的每个非本原特征标χ∈Irr(G)均可从极大子群诱导,所以在考察其拟本原性时,下述结论是很基本的,其意义在于明确指出了两个正规子群L和M,使得χ在其上的限制χL和χM,至少有一个是非齐次的。也就是说,在特征标限制不可约的条件下,非本原特征标一定是非拟本原的,所得结论是[2]中定理11.34的一个加强。 引理8设G为p-可解群,p为任意一个素数,H为G的极大子群且|G:H|为p的幂。假设χ∈Irr(G)和ξ∈Irr(H),满 足χ=ξG。 如 果ξL∈Irr(L),其中L=CoreG(H),则下述结论至少有一个成立: (1)χL是非齐次的。 (2)χM是非齐次的,其中K/L,M/K均为G的主因子。 证明如果H⊲G,则L=H。根据ξG=χ∈Irr(G)知,ξ在G中的惯性群Gξ=L,从而χL非齐次,此时结论(1)成立。 不妨设H⋪G,显然L 此时,不难看出CG(K/L)≥K,事实上CG(K/L)=K。这是因为:观察可知 [CG(K/L)∩H,K]≤L≤CG(K/L)∩H,表明K正规化CG(K/L)∩H,同时CG(K/L)∩H⊲H,所 以CG(K/L)∩H⊲HK=G。如果CG(K/L)>K,那么CG(K/L)∩H>L产生矛盾,故CG(K/L)=K。 由L 记φ=ξL∈Irr(L),假设(1)和(2)均不成立,那么φ是χL的唯一不可约分量。可令η∈Irr(M)是χM的唯一不可约分量。再令J=M∩H,并且δ=ξJ,选取θ∈Irr(K)为η在K上的一个不可约分量,如图1所示。 图1 特征标位置关系Fig.1 Position relations of characters 因为ξ(1)=φ(1)整除θ(1),而η(1)整除χ(1),故从 推出η(1)/θ(1)整除 |G:H|,从而也是p的幂,但η(1)/θ(1) 显然整除p'- 数|M:K|,只有η(1)/θ(1)=1,即ηK=θ。 上述表明θ是χ在K上的唯一不可约分量,则Gθ=G。根据下降定理可知θ与φ关于K/L出现下述三种情形之一:θL=φ,φK=θ或者完全分歧。如果θL=φ,根据引理1可知,χH=ξ,与ξG=χ矛盾。如果φK=θ,则Kφ=L与Gφ=G矛盾。因此θ与φ关于K/L是完全分歧的。 注意到δM=(ξJ)M=(ξG)M=χM=eη为齐次诱导,其中e为正整数,计算次数可知 观察可得 故上述不等式全取等号。根据[2,引理2.29]得,第一个不等式取等号当且仅当η(M−J)=0。同理,对每个g∈G均有η(M−Jg)=0。根据M/K是G-主因子,不难验证,从而η(M−L)=0,更有η(M−K)=0。此时我们有 1=[θ,θ]=[ηK,ηK]=|M:K|,矛盾。 有了上述准备,我们可证明本文定理1。 借助定理1,可证明本文定理2。1 预备知识

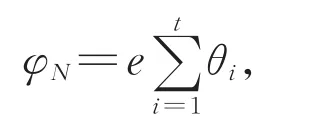
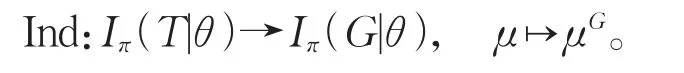
2 主要结果及其证明