面向多元时序关系的金融知识图谱表示与构建

高峰 ，郑丽丽 ，顾进广

（1.武汉科技大学 计算机科学与技术学院，湖北 武汉 430065；2.武汉科技大学 大数据科学与工程研究院，湖北 武汉 430065；3.湖北省智能信息处理与实时工业系统重点实验室，湖北 武汉 430065；4.富媒体数字出版内容组织与知识服务重点实验室，湖北 武汉 430065）

0 引言

金融行业支撑经济的迅猛发展，合理地运用金融知识对政府市场监管、异常监控、企业风险评估、投资决策等都有重要意义。但金融领域涉及数据多样，不仅包含了大量的企业、人群、市场监管等信息，还存在各实体之间的交易、投资等大量复杂关联和事件，而且受外界政经局势、天气变化等领域影响，面对近年来金融数据的爆炸式增长，传统的关系数据库存储方式已经满足不了“科技金融”[1]的需求，因此，基于知识图谱[2]的金融领域智能问答、语义搜索、辅助决策、智能分析等应用得到了关注。

但在传统的知识图谱结构中，两点之间的连接只能表示一对节点之间的二元实体关联。在现实金融领域中，面对大量复杂多元关系表示能力较弱，例如，金融领域的（债券）共同担保关系[3]，若以普通图表示这种关系，则多个担保者之间的“共同”性会被削弱。同时，现有知识图谱以静态的实体为核心，世间万物瞬息变化，现实世界中不断在发生着各类事件，动态的事件为社会实践提供参考并承载更深层次的信息。因此，对时序事件的通用化表示也是金融领域的重要需求。

基于以上需求，本文在现有的知识图谱表示机制上进行扩展，结合超图和超边的思想、规则推理[4]以及现有的时序逻辑表示机制，提出金融时序超图模型（Finanical Temporal Hyper⁃graph Ontology，FTHO①http://www.openkg.cn/dataset/ftho）。

1 相关工作

知识图谱是一种图结构的知识库，使用本体（Ontology）[5]对知识框架进行描述。在知识图谱发展的过程中，出现了一系列资源描述语言，例如RDF（Resource Description Framework）、RDFS（Resource Description Framework Sche⁃ma）、OWL，其中网络本体语言 OWL[6]为本体建模提供了属性特征描述和本体映射词汇，为知识图谱基于本体推理和基于规则的推理奠定了基础。例如：OWL：TransitiveProperty描述属性的传递性、OWL：SymmetricProperty描述该属性具有对称性等。伴随着金融智能化的提出与发展，因知识图谱在支持智能问答、辅助决策、智能分析等应用方面体现出卓越的优势，其在金融领域的应用也成为热门。

但目前对金融领域的复杂关系表示并没有合理解决方式，金融时序事件的通用化表示也没有确定的标准。基于现有问题，本文提出了金融时序超图表示模型，主要分为两点：一是对金融复杂关系超图的研究与拓扑结构表示，二是对时序金融事件模型的建立。

1）超图：二元关系是图结构中的基本研究对象，但随着各应用领域的发展，数据对象之间的关系也趋于复杂化，出现了大量类似一对多、多对多的复杂实体关联关系。普通图在描述类似复杂关系时体现出了局限性，因此，在1973年，Berge提出了超图概念，超图中的超边可以包含任意多个节点[7]，用来表示复杂的多元关系。根据金融领域复杂多元关系表示的困境，本文将超图理论应用于金融知识图谱的构建。

2）时序事件：事件描述主要要素为5W（Who，When，Where，What，Why）[8-10]，即描述某一时刻或某一时间段，一个或者多个角色参与的一个或多个动作组成的事情或者状态的改变。Silver等[11]在2011年提出了一种离散事件表示本体模型，提供了事件之间的关系表示方法。在2018年Hernes等[12]提出一种金融事件知识的语义表示方法。

2 金融本体模型

目前并无金融本体标准，为更好地说明本文所构建的金融时序超图中的概念，本文首先给出如图1所示的金融本体模型的简要版本，该金融本体来自现有金融领域数据中的重要概念及关联。该本体可不失一般性地作为金融时序超图概念的基础知识框架。

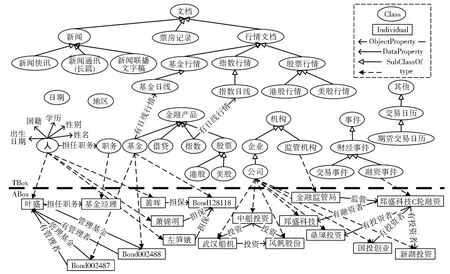
图1 金融本体模型Fig.1 Financial Ontology

金融本体模型共有178个类，分为9大模块：人、职务、金融产品、地区（GeoSparql）、机构、日期（OWL-Time②https://www.isi.edu/～hobbs/owl-time.html）、事件、文档和其他，各个模块又可分为不同的子类，例如金融产品的子类有基金、股票、指数、借贷等。同时，实体可以定义为某一类的实例，例如金融产品Shi⁃bor、Libor都属于借贷的实例。

类和实体都有数据属性描述其信息，例如人有姓名、性别、学历、国籍、出生日期等基本信息。本模型包含200个实体属性，描述了各类或各实例之间的关联，例如人与职务之间通过担任职务关联，叶盛担任职务为基金经理等。

3 金融时序超图拓扑表示模型

金融时序超图的拓扑表示模型分为超边模型、普通图拓扑表示模型和拓扑成分边到超边的映射规则三部分。金融时序超图拓扑表示模型以OWL语义为基础，使用二元关系来表示超图中的超边和内部节点的关系，并构建相应规则实现传统知识图谱的普通点、边到金融时序超图中的超边的映射。

3.1 超边定义

超图中的超边是属于该边的普通任意数目节点的聚合。如图2展示了一个普通图与超图对比实例，在此超图实例中节点集合V=｛V1，V2，V3，V4，V5，V6，V7｝，超边集合E=｛E1，E2，E3｝，E1=｛V1，V2｝，E2=｛V2，V3，V4｝，E3=｛V4，V5，V6，V7｝。

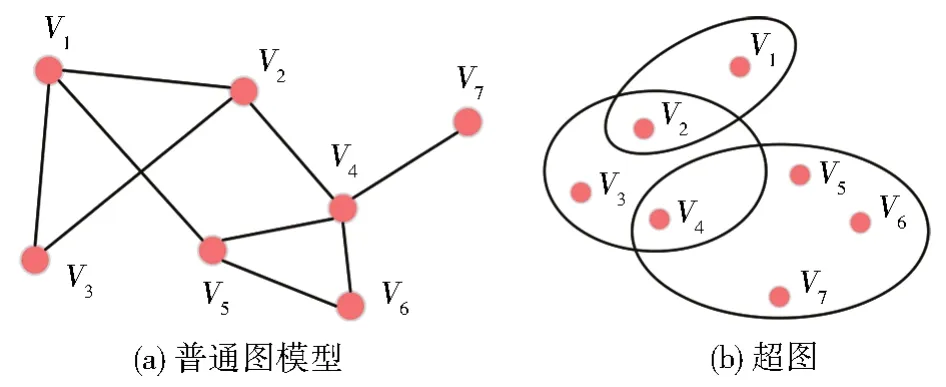
图2 普通图与超图实例对比Fig.2 Comparison of normal graph and hypergraph

如图2所示，从拓扑上来说，二元关系形成的普通图和多元关系形成的超图存在较大的差异。借鉴与RDF中容器的表示方法，根据超边内节点特性，将超边分为无序超边、有序超边和选择超边三类，分别基于RDF中的相应容器进行定义，如图3。

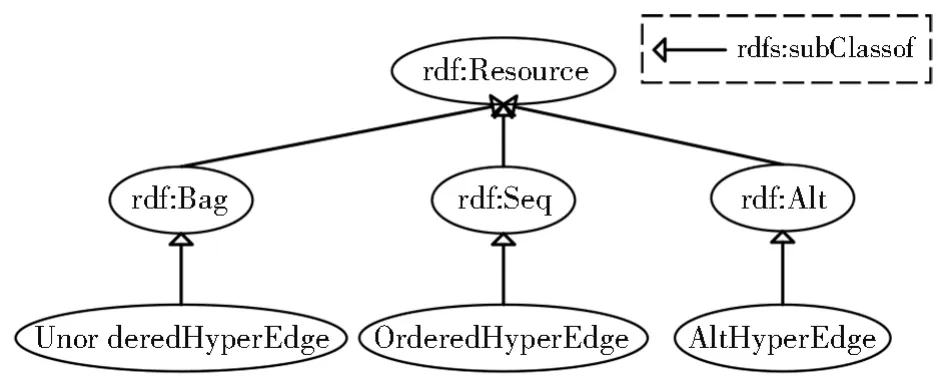
图3 金融时序超图中的超边定义Fig.3 Definition of hyperedge in the financial temporal hypergraph

3.2 超边构成成分的普通图拓扑表示

构成超图的普通边是具有传递性的边和具有共指性的边所形成的边的集合（子图），称这些普通边为“超边成分边”。超边成分边的传递性基于OWL提供的边的传递性（OWL：TranstiveProperty），共指性通过多边指向同一节点或来自同一节点得出。传递性边可形成链状子图或环状子图（图4（a）、4（b）），共指性边可形成星型内向子图或星型外向子图（图4（c）、4（d））。同时，由于传递性边具有方向，其形成的链状或环状子图可能形成有序或无序超边（图5（a）、5（b））。最后，根据传递性或共指性边是否可以存在于多个子图中，将构成超边的成分边分为融合成分边和共享成分边两类，其中融合成分边指其形成的链、环、星状子图中的任意一条成分边与其形成的超边之间不存在多对一关系（图6（a））；而共享成分边指其子图中的成分边与其形成的超边之间存在多对一关系，即成分边可为多个子图共享，所谓融合指构成此类结构的超边成分边都用于构造同一个超边，而共享指该超边成分边可以用于不同超边的构造中，如图5（b）中V2指向V7的成分边可为E1、E2、E3超边共享。

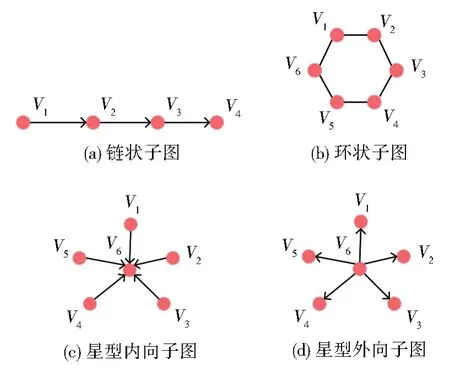
图4 普通图特殊拓扑结构Fig.4 Topological structure in graph

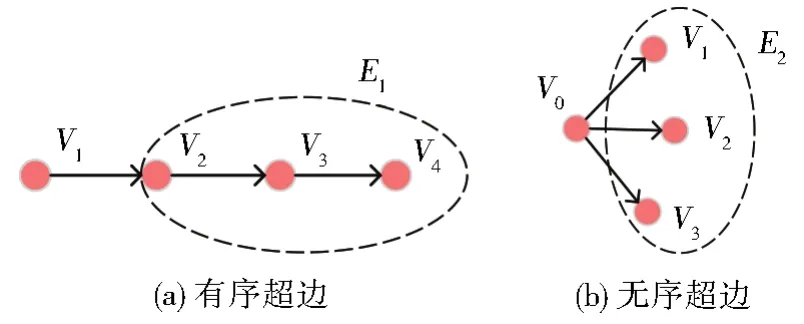
图5 普通图特殊拓扑结构构建超边Fig.5 Topological structure to build hyperedges

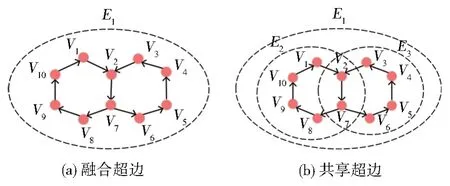
图6 融合超边和共享超边Fig.6 Inclusive hyperedge and share hyperedge

根据构成超边拓扑结构的普通边特性，超边成分边定义如图7所示，具体描述如下：

1）构成图4（a）有向链状子图的超边成分边定义为 orderedChainHyperEdgeComponent，根据其传递性和非对称性将其定义为OWL：Sym⁃metricProperty和 OWL：TranstiveProperty类型属性；将形成有向环状子图的超边成分边ordered⁃CircleHyperEdgeComponent定位为它的子属性。

2）不具有顺序性的链状子图的超边成分边定义为unorderedChainHyperEdgeComponent，并具有 OWL：AsymmetricProperty和 OWL：TranstiveProperty类型的属性；同理，构成如图4（b）无序环状子图的超边成分边定义为ordered⁃CircleHyperEdgeComponent。

3）因构成选择超边的内部节点的无序性，将构成选择链状子图的超边成分边定义为altChainHyperEdgeComponent，并且定义其为un⁃orderedChainHyperEdgeComponent的子属性。同时，当形成环状选择子图时，超边成分边定义为altChainHyperEdgeComponent。

4）构成图4（c）、4（d）的星形拓扑的具有共指性超边成分边分别定义为inwardHyper⁃EdgeComponent、outwardHyperEdgeComponent。

5）基于融合成分边和共享成分边的特性，构成图6（a）融合超边、图6（d）共享超边的超边成分边分别命名为inclusiveHyperEdgeCompo⁃nent、shareHyperEdgeComponent。

值得注意的是，以上超边和超边成分边定义不依赖于领域知识，任何金融领域知识图谱中的二元关系可以按照其内在特性被补充声明为以上超边成分边，从而利用下面的超边映射规则进行推理，并形成超边，从而可以保证模型的通用性。

3.3 超边映射规则和推理

超边可以直接由人工或者算法从源数据中定义或抽取，但更多的超边需要由对二元普通边进行连接性分析和子图构造得来。基于图3和图7中超边和超边成份边的形式和语义定义，本文得出如表1的规则集，用于自动化的超边生成。

图7 金融时序超图中的超边定义Fig.7 Definition of hyperedge in the financial temporal hypergraph

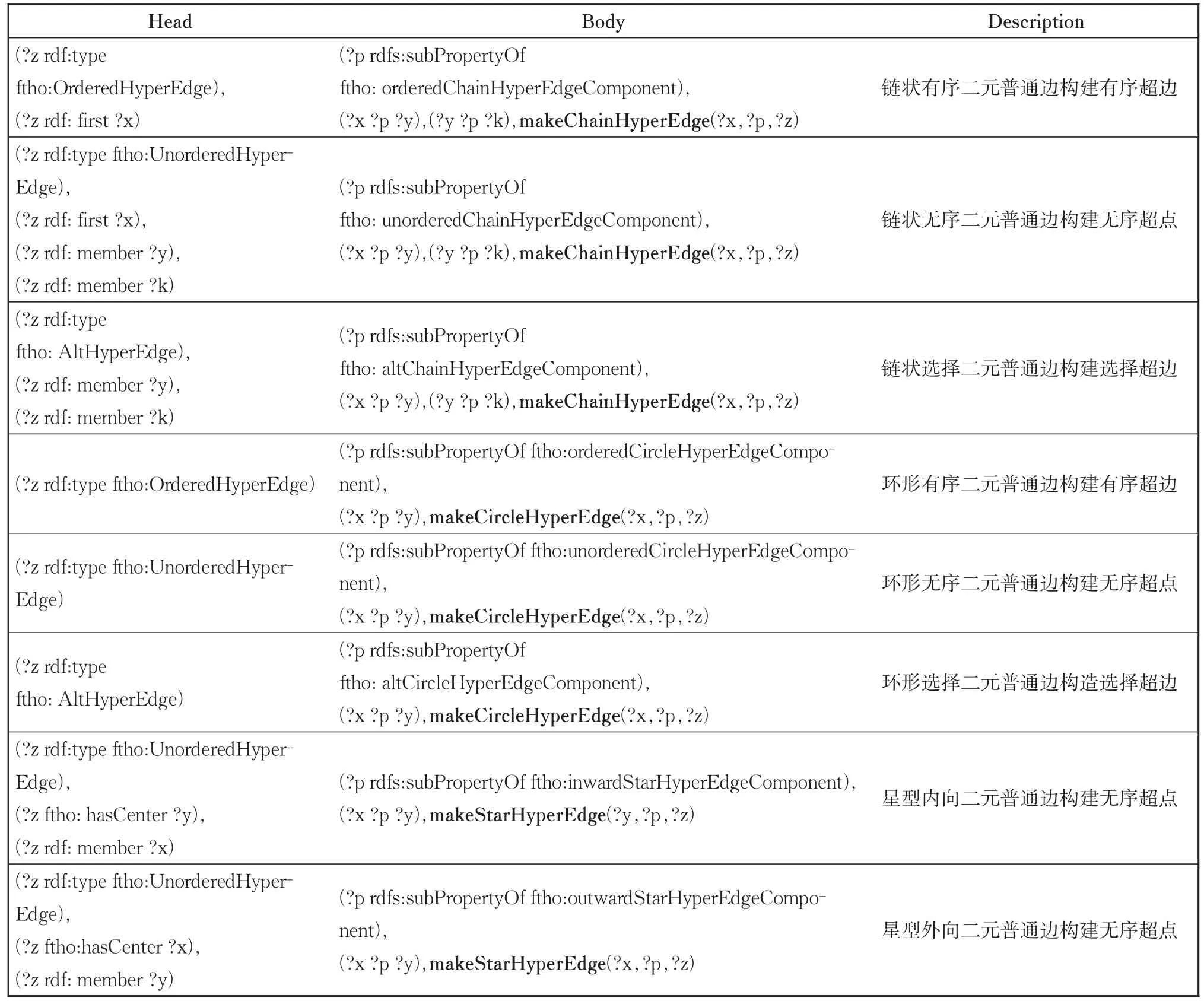
表1 时序金融超图中的超边构造规则Table 1 Hyperedge construction rules in financial temporal hypergraph

其中 makeChainHyperEdge、makeCircleHyper⁃Edge、makeStarHyperEdge是使用jena规则推理实现的自定义原语，主要目的是创建超边，并将超边与?z节点绑定。对三个原语的具体描述如下：

1）makeChainHyperEdge（?x，?p，?z）：当构成链状结构的普通边需要用到此原语时，首先，根据？x为链状结构起点特性，检验以?x-?p命名的超边是否存在，如果存在则直接将?z绑定该超边。若不存在，该原语会以?x为起点和?p为关系，不断寻找链中的下一结点，并?x-?p定义超边名称创建超边绑定给?z参数，最后，根据超边内部节点是否有序的特性，将链中各个节点以rdf：_n顺序或rdf：member无序方式放入超边中。

2）makeCircleHyperEdge（?x，?p，?z）：当构成环形结构的普通边需要用到此原语时，首先，检验该边构成的环对应的超边是否已经存在，如果存在则直接将?z绑定为此环对应的超边。若不存在，该原语会以?x为起点和?p为关系，不断寻找环中的结点，并且拼接各个节点名称与关系名称，例如：ftho：中船投资-风帆股份-武汉船机-circleShareholding，以此定义超边名称创建超边绑定给?z参数，并将环中各个节点放入超边中。

3）makeStarHyperEdge（?x，?p，?z）：当构成星型结构的普通边需要用到此原语时，检验该边构成的星型结构对应的超边是否已经存在，如果存在则直接将?z绑定为该超边。若不存在，根据?x为星型中心节点的特性，并且拼接?x与关系?p名称，例如：ftho：Bond128118-bond⁃TogetherGuarantee，以此定义超边名称创建超边绑定给?z参数。

4 金融时序超图事件时序模型

金融知识中的时间信息主要包含在事件中，因此，本文主要采用围绕事件的时序表示方法。事件时序模型使用事件概念和具化方法实现对金融事件时序的表示和推理。

4.1 事件时序表示

为了不失通用性，本文依据事件概念，将事件知识概括为事件元数据（包含时间信息在内）和事件内容两部分，其中事件元数据（包含事件概念本身）利用现有本体模型进行描述，包括使用GeoSparql来表示空间信息，使用OWL-Time来表示时间信息；而对事件内容采用RDF具化的方式来进行表述，这样，事件的内容可以是任何三元组知识。金融时序超图事件时序表示模型如图8所示。

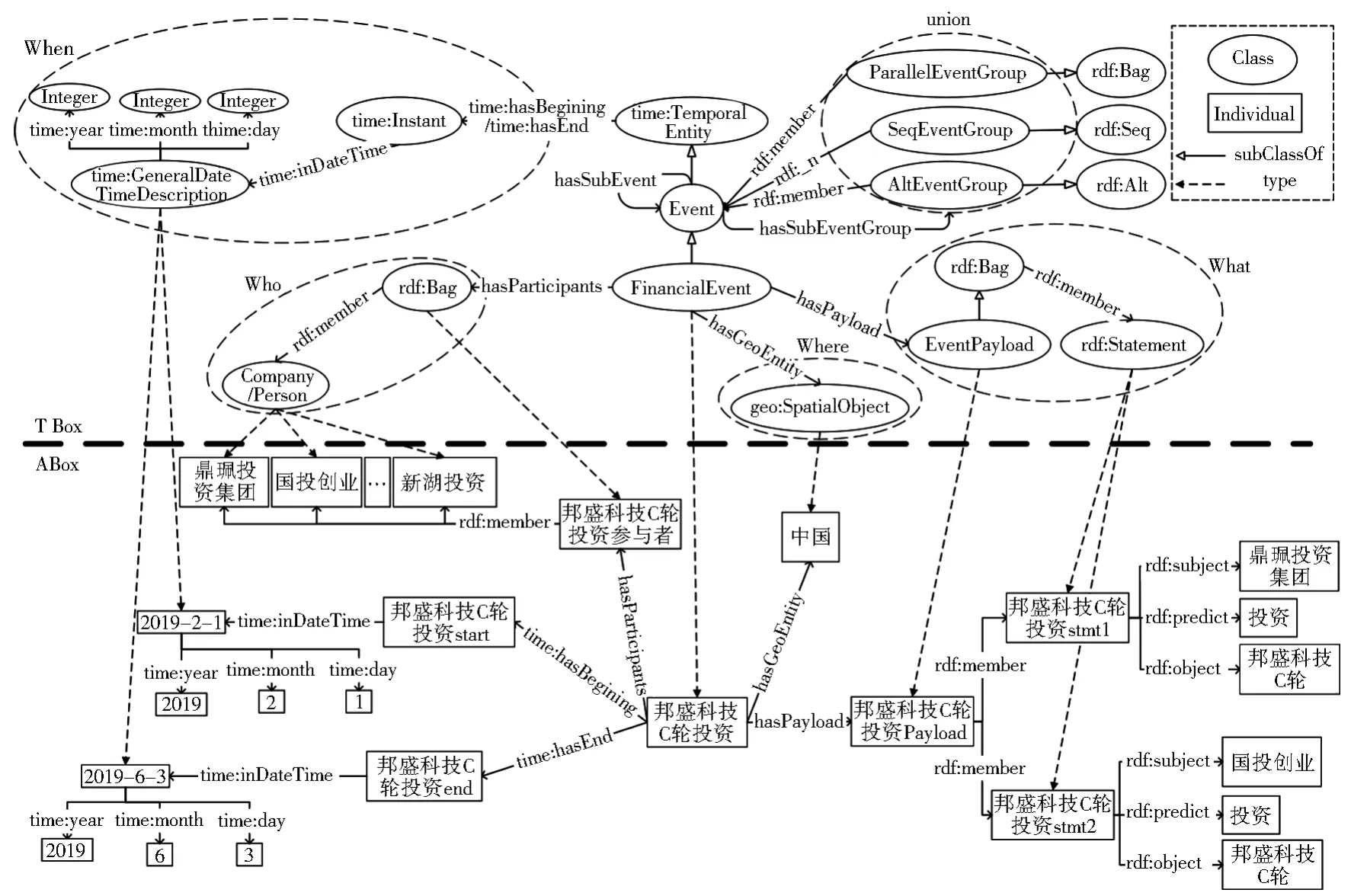
图8 金融时序超图事件时序表示模型Fig.8 Representation of temporal-event in financial temporal hypergraph

在事件核心概念中，FinancialEvent定义为OWL-Time中的TemporalEntity子类Event的子类。其主要拥有4类基本属性关联，hasGeoEn⁃tity用于连接事件和GeoSparql中的SpatialOb⁃ject，以描述空间信息；通过OWL-Time中的“hasBeginning”、“hasEnd”及其他属性，用于描述事件的时间；通过hasParticipants描述事件参与者，事件参与者使用无序集合（rdf：Bag）存储，可以任意多个人、公司等实体的集合；通过hasEventPayload描述事件内容，事件内容同样表示为一个无序集合（rdf：Bag），其中包含一系列的rdf：Statement用于表述事件知识，每个rdf：Statement使用三元组形式存储不可再分的事件原子内容。

除了以上四种基本属性以外，FinancialEv⁃ent还可通过hasSubEvent和hasSubEventGroup来实现事件的组合，即由一系列子事件嵌套构建复杂事件或复合事件。其中hasSubEvent主要用于无模式的事件组合，即事件的主从关系被定义，但是子事件的相互关联和事件模式未定义；而hasSubEventGroup通过对子事件的集合类型定义，来描述顺序模式（rdf：Seq），合取或析取事件模式（rdf：Bag）以及选择模式（rdf：Alt）。

4.2 事件时序表示规则推理

在定义了包含时序表示机制和事件组合机制的事件核心概念模型以后，本文通过定义如表2中的规则来进行时序推理支持。事件的时序推理主要体现在3个方面：1）事件元数据中的时序知识适用于事件内容中所有三元组的时序知识；2）超边的时序知识由其内部节点决定；3）组合事件的时序知识由其子事件聚合而来。

5 结果与分析

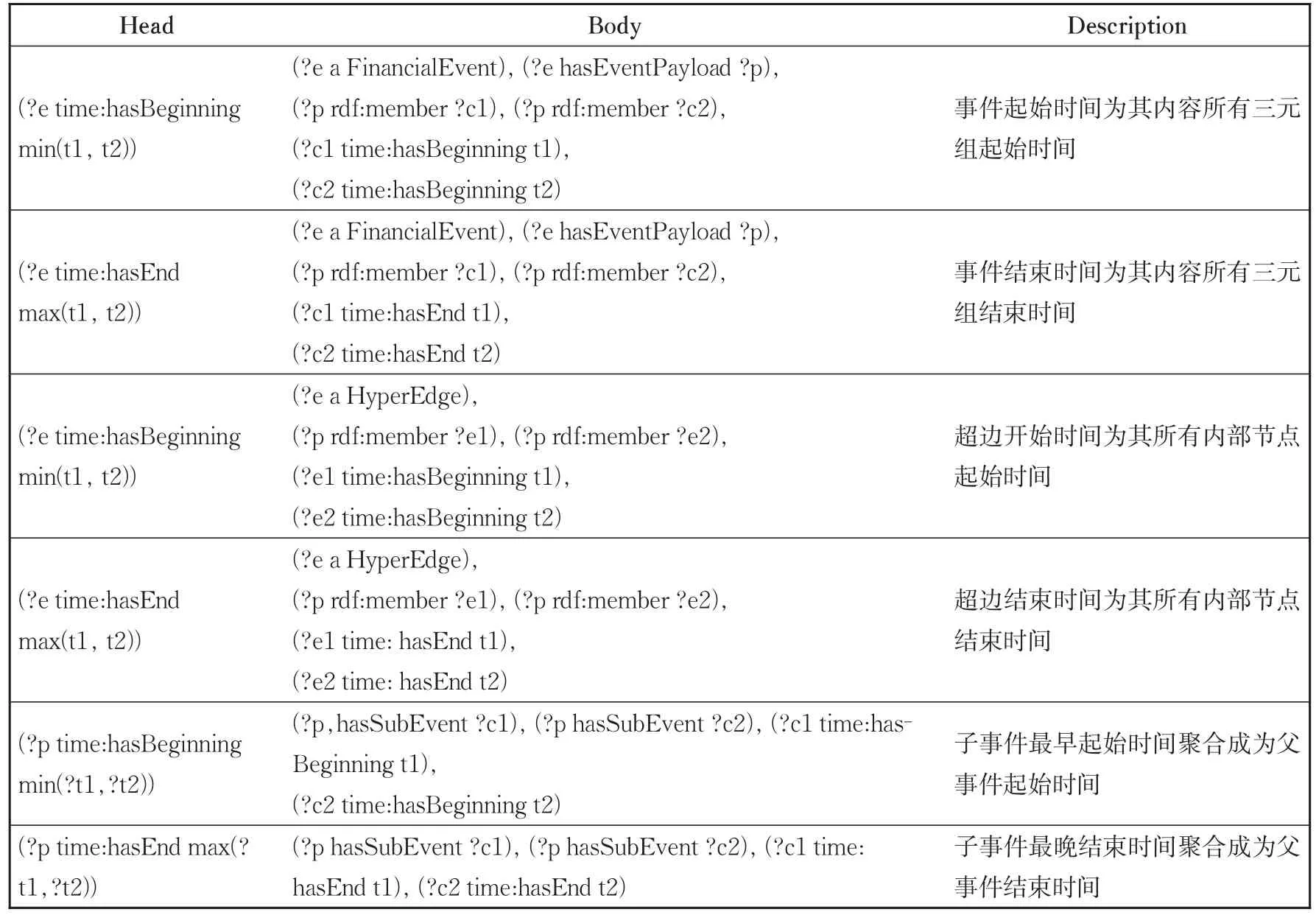
表2 时序金融超图中的时序推理规则Table 2 Temporal-event reasoning rules in financial temporal hypergraph

本文实验旨在实现构成拓扑结构的普通二元边至超边的映射规则推理、对比普通二元边与超边的检索效率、实现时序事件规则推理。本文建模工具为protege，使用Jena工具进行规则推理，通过SPARQL[13]语句进行检索。

5.1 实验数据

本文的实验数据主要来自互联网金融街、爱企查、企业预警通等相关权威数据源。基于以上对超图、普通图拓扑表示、时序事件表示的描述，结合OWL语义，将金融时序超图本体文件写入fin-temporal-hypergraph.owl文件，并将数据内容写入data.nt文件，将表1和表2的定义的规则写入myRules.rules文件。

本文以金融领域三种实际场景对金融时序超图拓扑表示模型进行实验；同时，针对事件时序表示模型的建模与推理，本文以图8邦盛科技C轮融资事件为例。对于拓扑表示模型，根据实际应用场景符合的拓扑结构，将实际场景实体间的普通二元关系定义为构成的对应拓扑结构成分边的子关系，下面将对三个实际应用场景进行描述，并在表3中对根据实际应用场景符合的拓扑结构，对其二元普通构成边进行定义描述。

1）（环形）交叉持股

交叉持股是指在不同企业之间互相持股的现象，交叉持股很可能导致不同企业之间进行利益输送[14]，因此对于交叉持股现象的监督是金融领域的重点。本文对实际场景中环形交叉持股现象进行验证，图9为环形交叉持股实例。

图9 环形交叉持股实例Fig.9 Example of circular share-holding

2）一人兼多家公司董事

董事在法律上掌管着公司财产，执行着股东会决议，拥有公司事务的自由裁量权[15]。在实际场景中，一人可以兼任多家公司的董事，符合星型向外拓扑结构，图10为一人兼多家公司董事的实例。

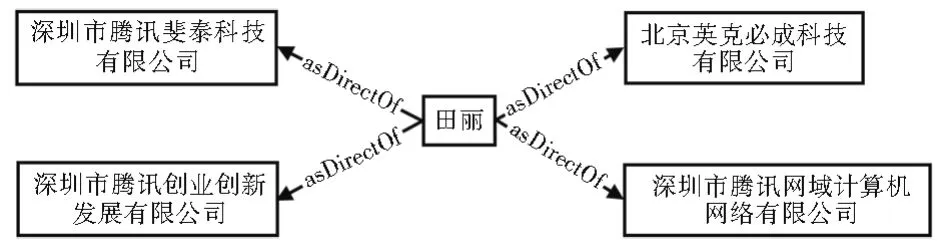
图10 一人兼多家公司董事实例Fig.10 Example of one person serving as directors of multiple companies

3）（债券）共同担保

在金融领域，一项债券可由多个担保人共同担保，符合星型向内拓扑结构，图11为债券共同担保实例。

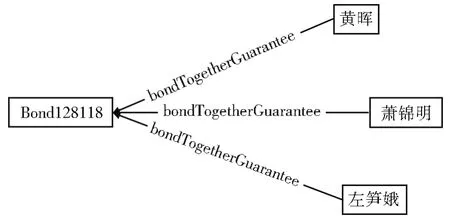
图11 债券共同担保实例Fig.11 Example of bond co-guarantee

5.2 实验及结果分析

5.2.1 实验过程

为验证金融时序超图的可行性与检索效率，使用jena工具首先读取fin-temporal-hyper⁃graph.owl文件中的本体和data.nt文件的数据构建推理前的金融时序超图，再读取myRules.rules文件的规则集，通过jena规则推理机推理后得到完整的金融时序超图。

5.2.2 金融时序超图可行性验证

基于规则推理之后的金融时序超图，使用SPARQL语句进行拓扑模型普通二元关系和超图超边的查询对比、事件时序模型原子级内容的时间查询。查询样例如图12所示，其中已省略前缀，ftho代表本文创建的金融时序超图模型。

图12 金融时序超图SPARQL查询语句Fig.12 SPARQL query statement in financial temporal hypergraph

以图12（a）（环形）交叉持股、图12（c）（债券）共同担保、图12（d）时序事件表示模型的事件内容时间推理为例，查询结果分别为表4−6所示。

表3 金融领域实际应用场景关系定义Table 3 Definition of practical scenarios in the financial field

表4 （环形）交叉持股查询结果Table 4 Query results of circular share-holding

表5 （债券）共同担保查询结果Table 5 Query results of bond co-guarantee

5.2.3 多元关系查询效率对比

本文在以上查询过程中，同时记录了不同现实场景通过普通边方式和超边方式检索所需要的时间，对比结果如表7所示。

超边的构建不仅可以解决多元关系的复杂表示问题，根据以上检索时间对比表明，在检索效率上，超边的检索时间仅仅是普通二元边检索的1/20，极其显著地缩短了查询时间。因此，在构建金融时序超图后，可将超边作为索引进行图检索，大大提高了检索效率。

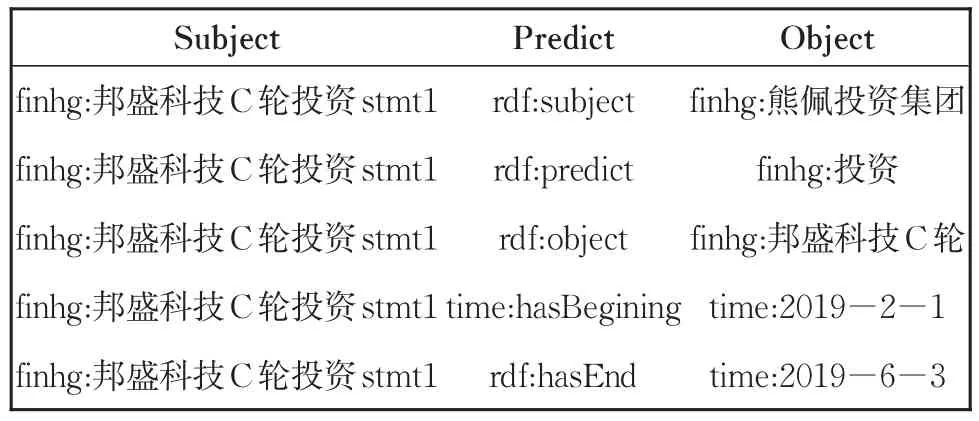
表6 事件内容与时序查询结果Table 6 Query results of event playloads and time

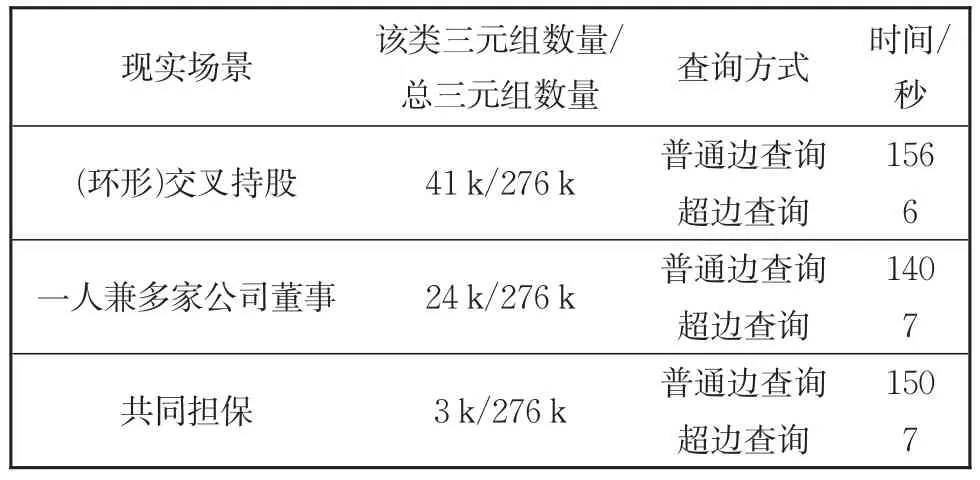
表7 普通边与超边检索时间对比Table 7 Comparison of retrieval time between normal edge and hyper edge

6 结论

本文从金融领域实际应用场景出发，扩展现有知识图谱表示机制，构建了金融时序超图。本文主要工作分为两个部分：首先，将现实场景中复杂的多实体关联关系抽象为拓扑结构，并根据其结构特性，建立拓扑子图的二元构成边节点映射超边的规则集，再通过规则推理方式，实现二元关系构成的拓扑结构到超图的映射。其次，本文建立了通用化的金融时序事件表示模型。对于事件元数据，使用现有本体模型进行表示，例如，使用GeoSparql来表示空间信息，使用OWL-Time来表示时间信息。对于复杂的事件内容，使用灵活的三元组具化方式进行表示，当事件内容包含超边成分边时，事件的时序知识即可传导到超边上，实现多元时序信息的融合表示和推理。此外，由于多元、时序知识表示和推理规则与具体领域知识的解耦，本文的模型可以适用于现有的金融领域知识图谱。

基于真实数据集的实验结果表明，本文模型不仅满足金融领域多元关系表示需求，且以超边建立索引，检索效率比普通二元关系提高近20倍。另外，金融时序事件模型可通用化表示为事件五元组（When，Where，Why，What，Who），再通过规则推理，得出事件内容中的原子事件的时间信息，因此，本文模型可为事件推理、潜在信息挖掘提供基础。

本文的金融时序超图的研究工作仍有一定的改进空间，未来的工作主要分为两方面：1）本文虽对复杂多元关系抽象的拓扑表示定义较全面，但金融领域发现的实际应用场景的多样性不足，下一步应加深对金融领域业务的了解，挖掘更多现实世界中复杂多样的多元关系。2）基于本文提出的通用化时序事件表示模型，更全面的事件时序推理、因果关系推理等，值得进一步研究。