基于R语言ARIMA乘积季节模型预测医院手术量

曹丙艳

山东第一医科大学第二附属医院，271000 山东 泰安

手术量是医院业务工作量的一项重要统计指标，它不仅反映就医群众对医院医疗技术水平和医疗服务的认可，同时也是体现医务人员劳动价值的重要指标。对手术量进行科学准确的统计预测，可以帮助医院和临床科室提前做好医疗资源配置，提升工作效率，还可为医院管理者制定临床科室下一年目标值提供参考依据。本研究运用某医院2016年1月至2021年12月手术量资料，基于R语言自回归移动平均乘积季节模型（auto-regressive integrated moving average，ARIMA）［1］选择最优模型，进行手术量短期预测。

1 资料与方法

1.1 资料来源

数据来源于某医院统计管理信息系统，从系统导出2016年1月至2021年12月手术量统计报表。2016年1月至2020年12月手术量用R 4.1.3软件进行ARIMA乘积季节模型建模，用2021年1月至12月手术量评价模型预测效能，外推预测2022年上半年的手术量。

1.2 研究方法

本研究运用ARIMA（p，d，q）（P，D，Q）s模型建立手术量的数学模型。其中，p、d、q分别为自回归阶数、非季节差分阶数、移动平均阶数；P、D、Q分别代表季节自回归阶数、季节差分阶数、季节性移动平均阶数；s为周期［2］。

ARIMA模型建模的基本步骤［3-6］：

1）时间序列的平稳化。先对原始数据制作时序图、月度图观察数据变化规律，绘制自相关图（autocorrelations function，ACF）、偏自相关图（partial autocorrelations function，PACF），用adf.test（）函数验证有无单位根。如果数据存在趋势性和季节性，对数据进行趋势差分、周期性差分，将数据转换为无长期趋势性和周期性的平稳序列。

2）模型识别。对平稳后的数据，绘制ACF图和PACF图，根据其截尾或拖尾的情况识别模型中p、q、P、Q的数值，拟合1个或多个ARIMA模型，用R 4.1.3软件中auto.arima（）函数自动选取AIC和BIC最小模型，与ACF图和PACF图建立的模型进行比较。

3）参数估计和模型诊断。对模型残差进行Ljung-Box残差白噪声检验（L-B检验），以判断模型中的信息提取是否充分，再通过比对备选模型的池赤信息准则（Akaike information criteri-on，AIC）值，在所有通过检验的模型中，依据AIC函数达到最小的模型为相对最优模型。

4）模型验证及预测。利用选出的最优模型进行验证并预测，将2021年手术量的实际值和预测值进行比较，使用平均相对误差（mean absolute percent error，MAPE）评价模型的准确性，并预测2022年上半年手术量。

2 结果

2.1 数据平稳化

2016—2021年医院手术量呈明显上升趋势，且呈现季节性，说明时间序列不平稳。每年的2月是医院手术量低谷时期，每年的7月、8月是医院手术量高峰时期，且2020年2月手术量低于2016年以来历年同期水平。见图1、图2。运用R 4.1.3软件中ndiffs（）函数进行差分判断后，用diff（）函数对原始数据进行一阶差分，消除时间序列的趋势和季节影响，使用tseries包中的adf.test（）函数检验（P=0.01），由此可知差分后数据满足平稳性要求。

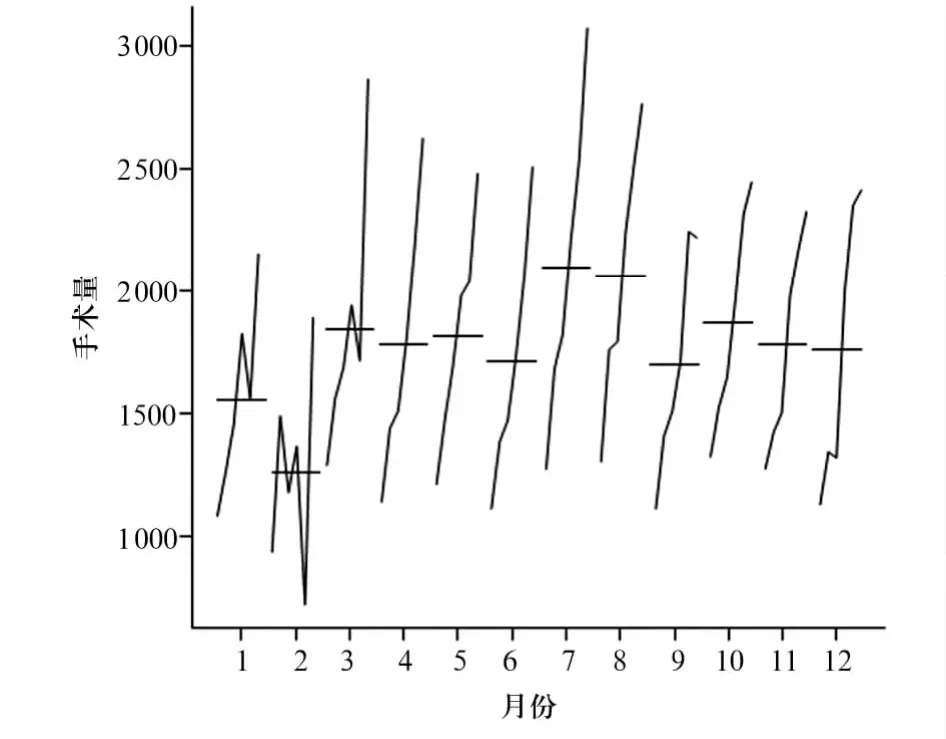
图1 2016—2021年手术量月度情况

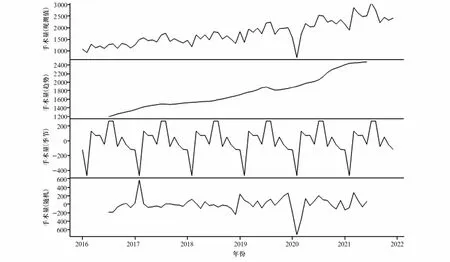
图2 2016—2021年手术量时序分解图

2.2 模型识别

经过一次一阶差分后ACF图和PACF图见图3。根据一次一阶差分后的自相关图得知，自相关系数一阶截尾，q=1，偏自相关2阶后减为0；从周期来看，ACF一阶后减为0，PACF一阶后截尾，P=1，初步确定模型中ARIMA（p，1，1）（1，1，Q），p的备选参数0，1，2，Q的备选参数0，1。用R 4.1.3软件auto.arima（）函数自选模型是ARIMA（3，1，0）（1，0，0）12。

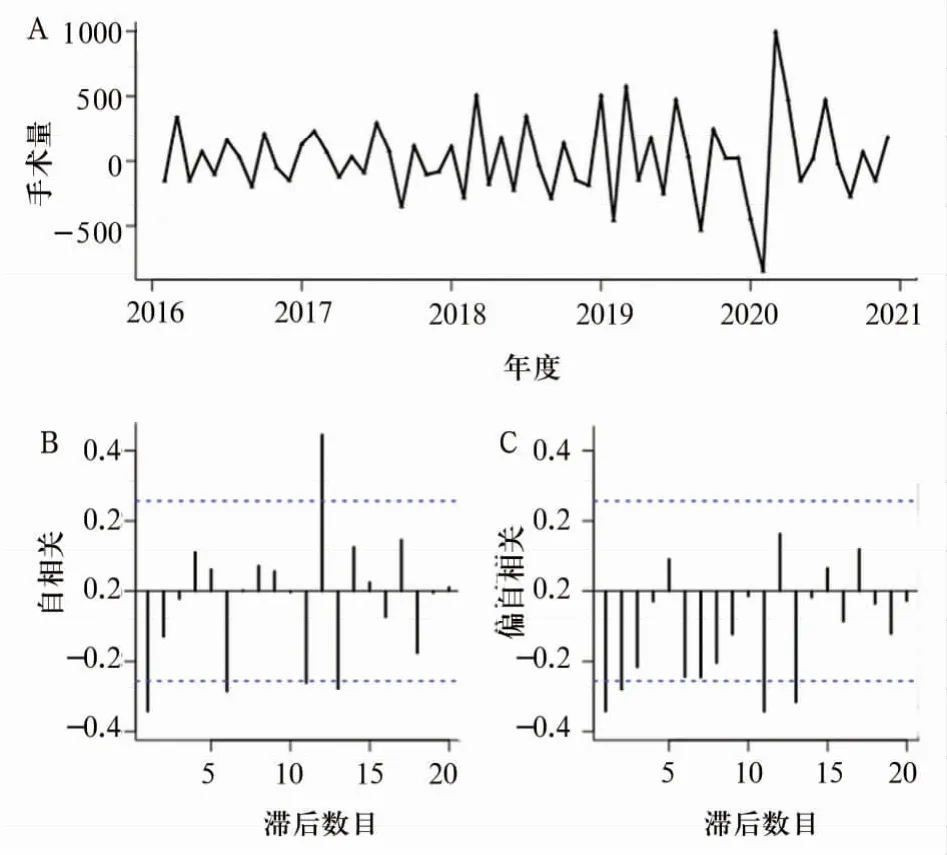
图3 一阶差分后的分析图

2.3 模型诊断

用arima（）函数对ARIMA（p，1，1）（1，1，Q）中p的备选参数0，1，2，Q的备选参数0，1由低到高逐个测试，P值有意义的模型是ARIMA（1，1，1）（1，1，0）12，ARIMA（0，1，1）（1，1，0）12，把测试后的模型和R软件自选模型ARIMA（3，1，0）（1，0，0）12用box.test（）函数进行Ljung-Box残差白噪声检验，以AIC最小作为依据确定最优模型。见表1。

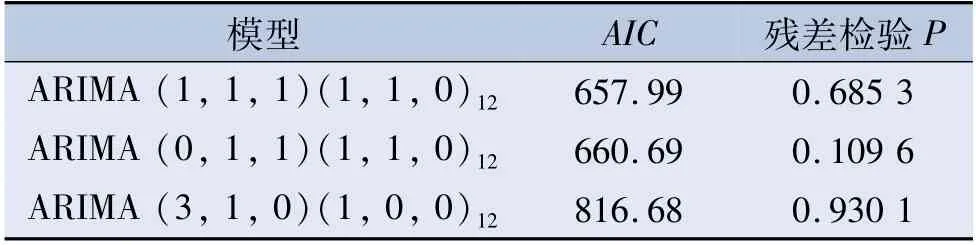
表1 模型确定信息情况

2.4 模型验证及预测

用forecast（）函数对ARIMA（1，1，1）（1，1，0）12模型进行2021年1月至12月手术量预测，平均相对误差是7.71%。手术量实际值除2月、3月外，其他月份全落在了95%置信区间内，说明模型预测效果良好，见表2、图4。用ARIMA（1，1，1）（1，1，0）12模型预测2022年上半年的手术量，2022年上半年手术量继续增长，见表3、图4。

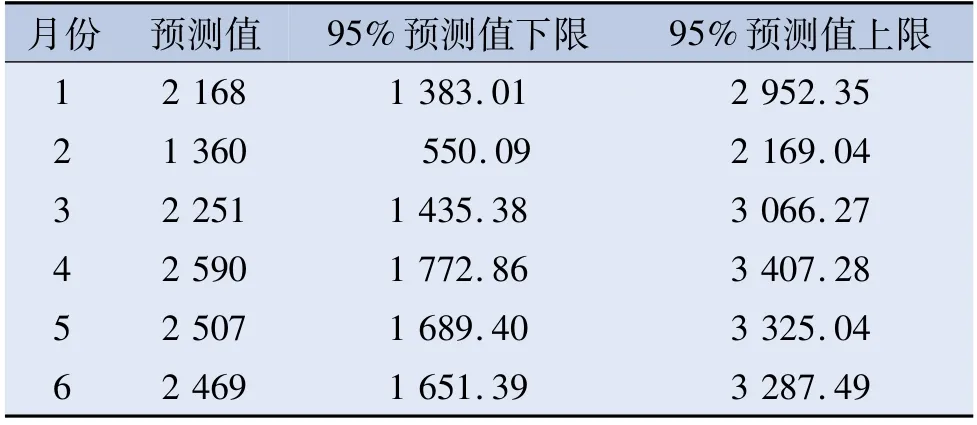
表3 2022年某医院上半年手术量预测值

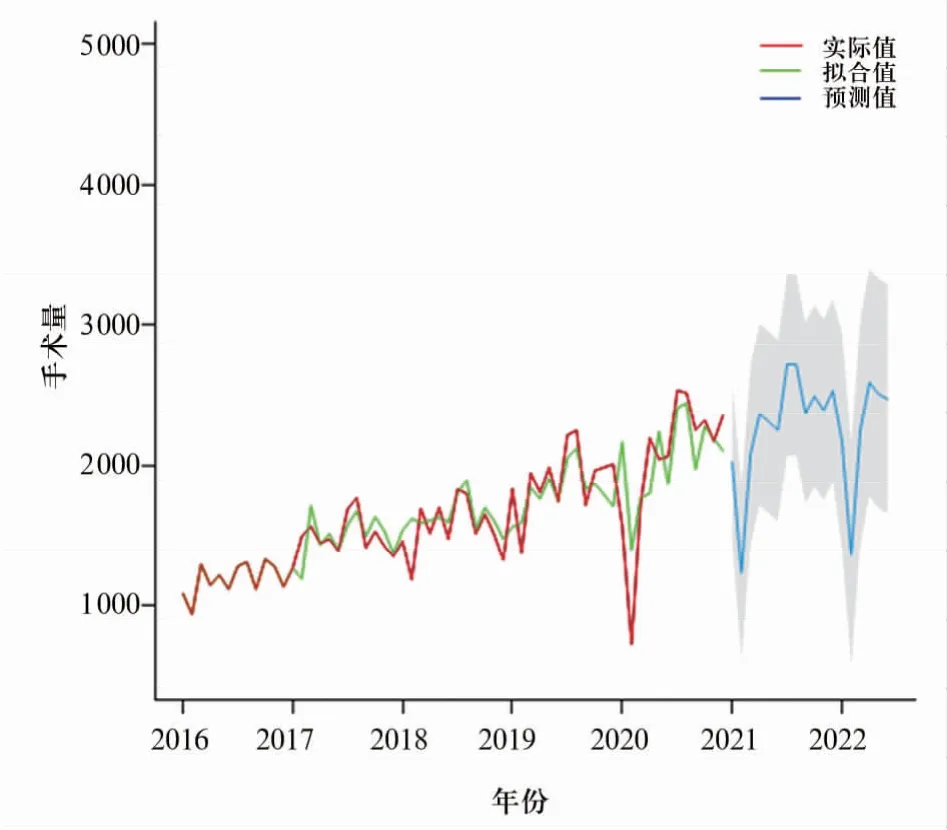
图4 某医院手术量预测图

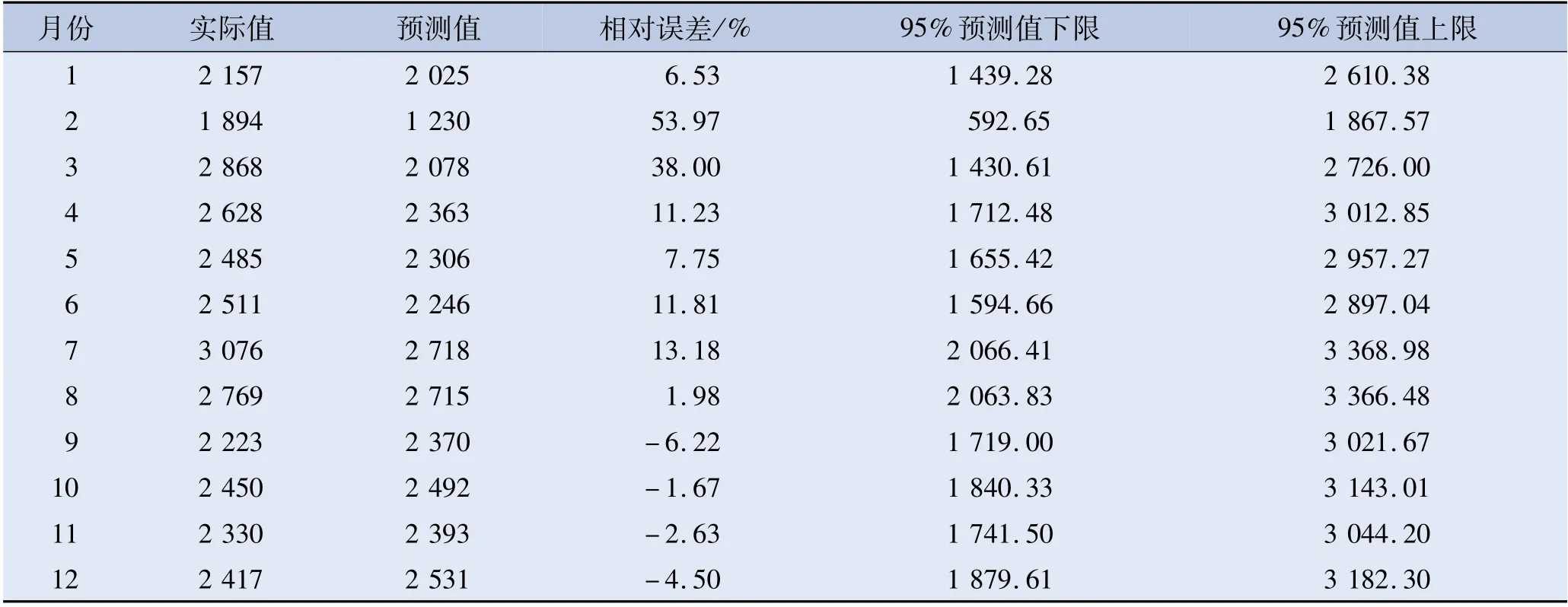
表2 2021年某医院手术量实际值与真实值比较

3 讨论

通过数据分析可知，某院手术量呈明显上升趋势且呈现季节性，每年的2月手术量最少，7月、8月手术量最多。主要原因是2月一般恰逢春节，受习俗的影响，只要不是危、急、重患者，一般等过了春节就医；7月、8月手术量多，主要原因是学生在放假期间，小儿外科、口腔科、眼科手术病人数量相对增加。医院管理者应结合手术量实际情况，在手术量低谷时期，组织科室人员进行业务学习，外派进修人员学习先进医疗技术；在手术量高峰时期，要加大医疗资源的投入，适当增加相关科室的医务人员数量，保证手术能够安全高效地进行。

本研究运用R语言软件，利用2016年1月至2020年12月手术量建立ARIMA（1，1，1）（1，1，0）12模型，用该模型对2021年1月至12月手术量进行预测，手术量的实际值与预测值的平均相对误差7.71%，说明预测结果良好，可以用于外推预测。但2021年2月、3月实际值超出了95%置信区间，由于2020年2月、3月受新冠肺炎疫情影响严重，手术量低于历史前期水平，出现模型预测时预测值偏小的情况。

ARIMA模型是将多种因素的综合效应蕴含于时间变量之中，不用考虑影响预测变量的相关因素，通过对模型反复识别和修正达到最满意的预测模型［7］。ARIMA模型预测，只适合短期预测，不能进行长期预测；要继续进行后期预测，需要不断地更新数据，用添加后的数据不断地修正或重新建立预测模型，才能得到更好的预测结果。

统计预测是现代医院管理的一种科学手段和方法，ARIMA模型不仅可以用于预测，还可以用于目标值的制定。选择适合自己医院的统计预测模型，可以为医院合理配置资源，提高工作效率，提升服务质量，还可以为医院管理者进行更好的管理和决策提供有利依据［8］。