连续搅拌釜式反应器的自耦比例–积分–微分控制

白家赞,曾喆昭

(长沙理工大学电气与信息工程学院,湖南长沙 410114)

1 引言

CSTR常用于药物、涂料、化肥等的生产,在化工生产领域中有着重要的地位.CSTR系统是典型的非线性化学反应系统,对该系统状态调节有一定难度.近年来国内外学者也提出许多了针对CSTR系统的状态调节方法,并取得了较好的效果,如:模型预测控制[1–3]、神经网络控制[4–6]、模糊控制[7–8]、滑模控制[9–11]、智能PID控制[12–15]、模型优化控制[16]、最优控制[17]等.其中,文献[1]所使用的模型预测控制方法,控制器参数较多,结构较为复杂,且响应速度相对较慢,存在超调现象.文献[6]所使用的鲁棒自适应神经网络控制方法响应速度较快,然而控制器参数较多,结构较复杂,且控制信号存在抖振现象.文献[7]中所提出的多误差模糊控制方法涉及多个控制力之间的切换,控制器结构较为复杂,且控制信号存在抖振现象.文献[10]所提出的自适应准滑模控制方法响应速度较快,然而控制器增益较大,且计算量较大,使得控制器设计成本提高,CSTR系统输出存在超调现象.文献[13]所提出的基于混沌萤火虫算法的分数阶PID控制方法可以得到较好的控制效果,然而其仿真表明该方法需要经过近100次的迭代后才能达到最佳效果,且计算量较大,控制器结构复杂.文献[14]所使用的自适应模糊增益PID控制方法取得了较好的控制效果,然而该方法将3个不同的控制器输出组成一个总的控制输出,使得控制器结构复杂,计算量较大.为更好的满足工业实际,设计简单有效的CSTR状态调节器尤为重要.由于CSTR系统非线性的特点,且实际生产中始终存在的反应物浓度变化、副反应、温度变化以及外部扰动等因素均会影响CSTR系统的状态调节效果,因此提高控制系统的鲁棒稳定性和抗扰动鲁棒性,是改善CSTR控制效果的关键.

本文针对一类非线性不确定CSTR系统,使用了一种ACPID控制器[18],该控制器使用了一个与被控系统无关的“速度因子”形成的ACPID镇定规则,将比例、积分、微分3个控制力耦合起来,使得比例、积分、微分3个功能各异的控制力在控制过程中能够表现出目标一致的协调的控制行为.ACPID控制方法动态品质较好:响应速度快、无超调,且控制器结构简单,仅涉及一个“速度因子”的镇定,可广泛应用于CSTR系统状态调节领域.此外,文献[19–20]根据PID控制系统的物理属性分析,科学阐述了无量纲的比例增益是引起PID增益鲁棒性差与抗扰动鲁棒性差的理论根源,并科学解释了ACPID控制器遵循量纲匹配的规则.

本文根据ACPID控制理论思想来实现CSTR控制方法,获得了良好的控制效果,进一步表明了ACPID控制系统具有良好的鲁棒稳定性和抗扰动鲁棒性.

2 CSTR过程描述

2.1 CSTR的数学模型

CSTR是一类典型的非线性系统,其中一阶不可逆反应(A→B)的CSTR系统如图1所示.

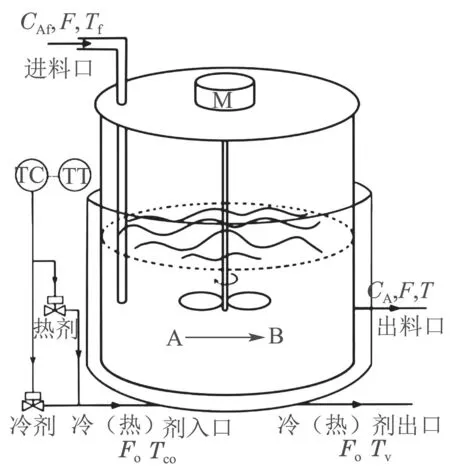
图1 CSTR系统Fig.1 CSTR system

CSTR动态方程如下:

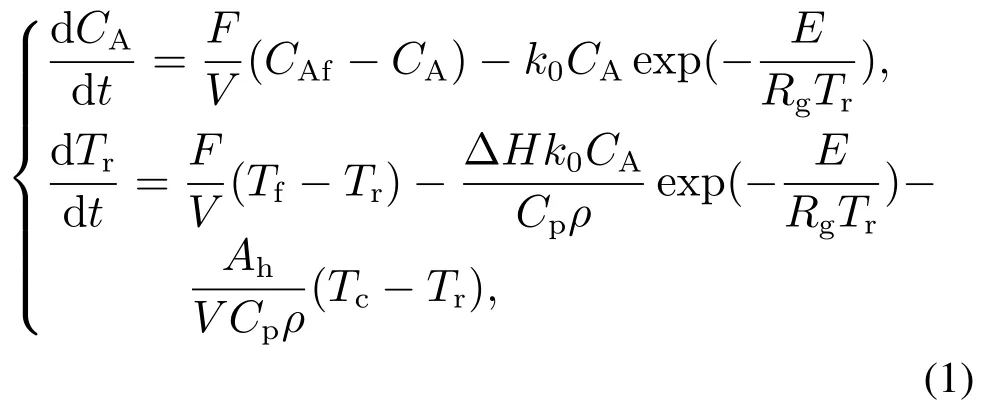
其中:CA为反应浓度;Tr为温度;操作的控制变量Tc为冷却剂温度.

根据Uppal等的分析[21]引入如下参数无因式化模型

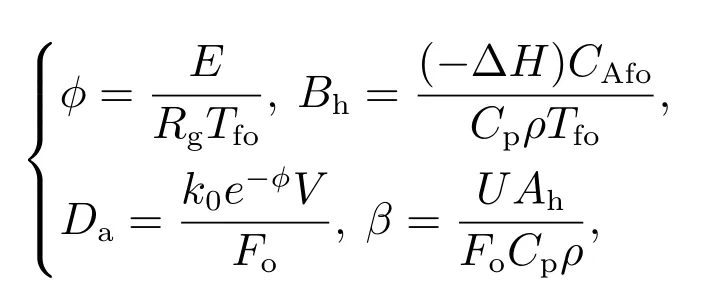
其中:Fo为过程流量;CAfo为进料浓度;Tfo为进料温度.

定义无因式变量

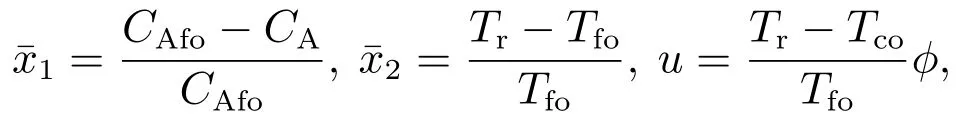
其中Tco是冷却液温度的参考值.

无因式化后CSTR模型可改写为

2.2 CSTR系统映射

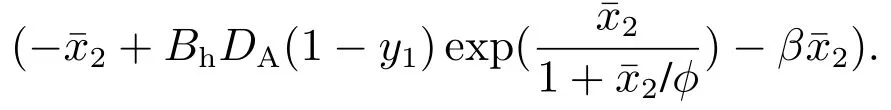
显然,系统(3)是未知的二阶线性时变系统,且与系统(2)等价.其中,总扰动包含了系统(2)中所有已知或未知的复杂因素.

3 自耦PID状态调节器

3.1 自耦PID状态调节器的设计

设期望输出为yd,系统的实际输出为y,定义系统误差e1为

其中定义zc>0为速度因子(量纲:1/s).

由式(9)所表示的ACPID镇定规则实质上是量纲的换算规则,根据ACPID控制理论思想[19],定义受控误差系统的比例控制力、积分控制力、微分控制力分别 为.显然,引入速度因子后,3个功能各异的控制力有了相同的量纲,并建立了内在关系.由各控制力相加组成的ACPID控制力表示为

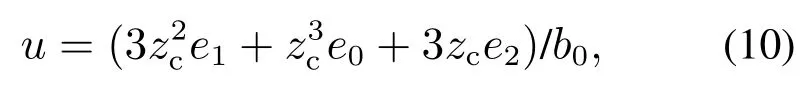
其中|u|≤2.

3.2 稳定性分析

定理1当,且zc>0时,ACPID状态调节系统是大范围鲁棒稳定的,不仅稳态误差有界:,而且ACPID状态调节系统还具有良好的抗扰动鲁棒性,理论上可以实现零误差跟踪控制.

证把式(10)代入式(8)可得ACPID闭环状态调制系统如下:

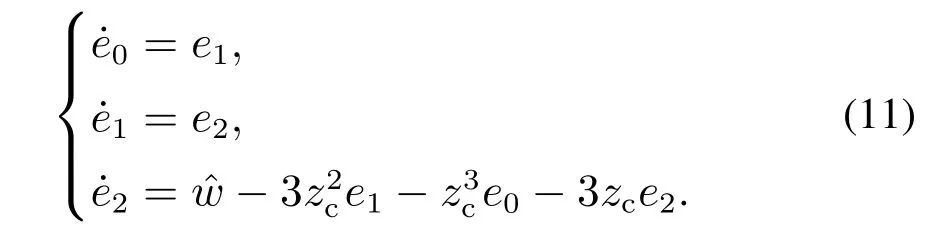
由式(11)可知,ACPID状态调节系统是在未知有界扰动激励下的误差动态系统.对系统(11)取拉普拉斯变换可得

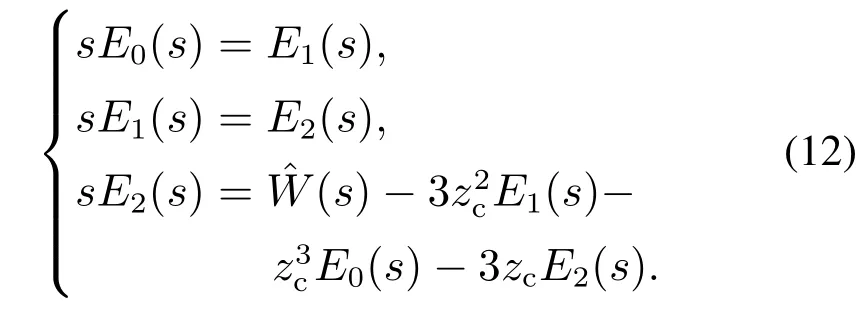
由式(12)可得该闭环控制系统为

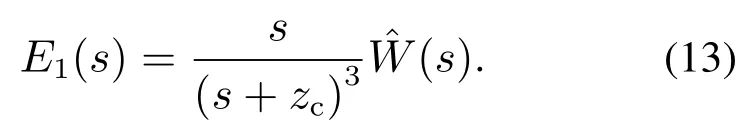
故受控误差系统的传递函数H(s)为

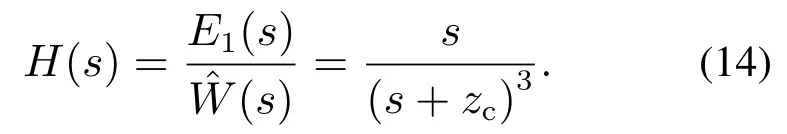
由式(14)可知,当zc>0时,受控误差系统的三重极点位于s域的左半平面内,因此ACPID状态调节系统(11)是大范围稳定的.又因为zc与CSTR系统模型无关,因此ACPID状态调节系统(11)是大范围鲁棒稳定的.

由式(14)可得冲激响应h(t)为

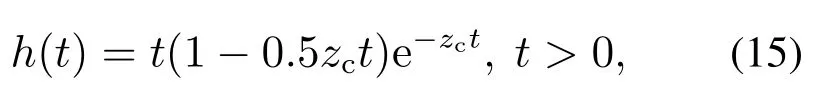
其中e≈2.718是自然对数的底.

由式(13)–(15)可得受控误差系统的时域解为

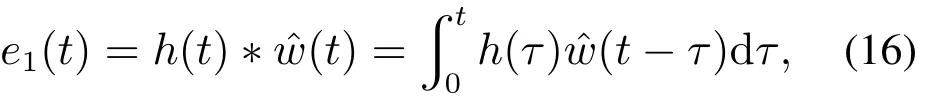
其中式中的“∗”为卷积积分运算符.

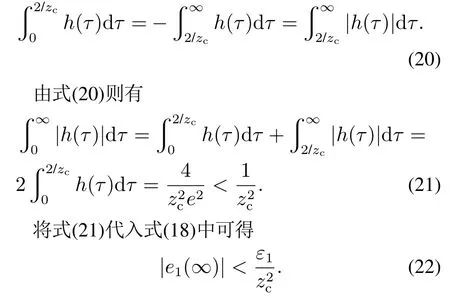
由式(22)可知:稳态误差只与复合扰动的上界和速度因子有关,与被控系统的具体模型无关,因而ACPID状态调节系统具有良好的抗扰动鲁棒性.此外,稳态误差随速度因子的增加而呈平方倍减小,当zc→∞时,|e1(∞)|=0,因而理论上可实现零误差跟踪.

证毕.

4 仿真实验及分析

为验证本文方法的有效性,对CSTR系统进行仿真实验.为了便于比较,系统相关参数与文献[22]完全相同:Da=0.072,ϕ=20,Bh=8,β=0.3,系统的稳定状态如表1所示;设系统初始状态为[x1(t0),x2(t0)]=[x1d −0.1,x2d −0.3];设ACPID控制器的速度因子为zc=26,仿真时间10 s,本文仿真结果如图2–4所示,文献[22]的结果如图5–7所示.

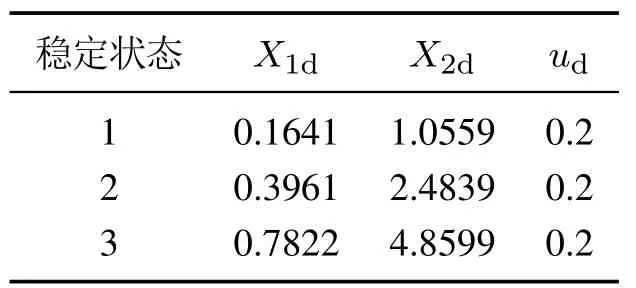
表1 CSTR的稳定状态Table 1 Steady state of CSTR

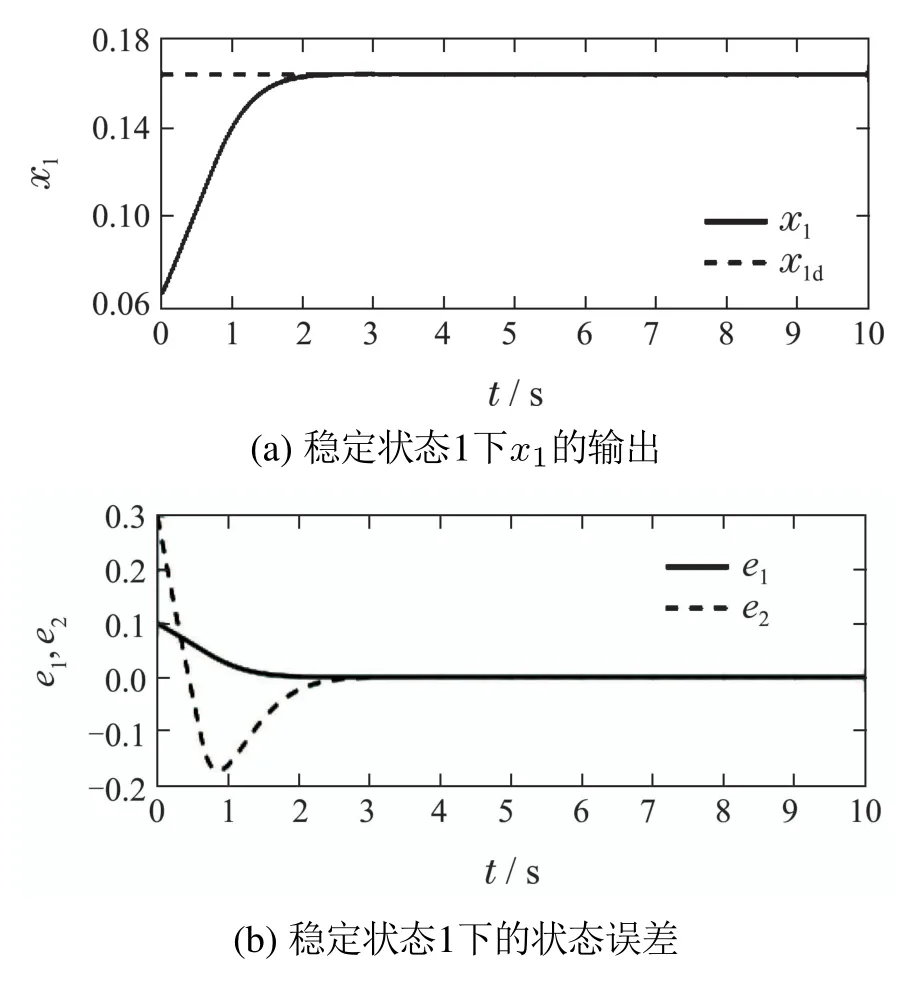
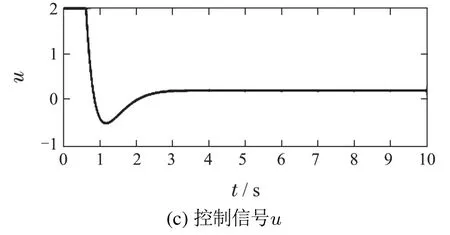
图2 稳定状态1仿真结果Fig.2 Simulation result of state 1

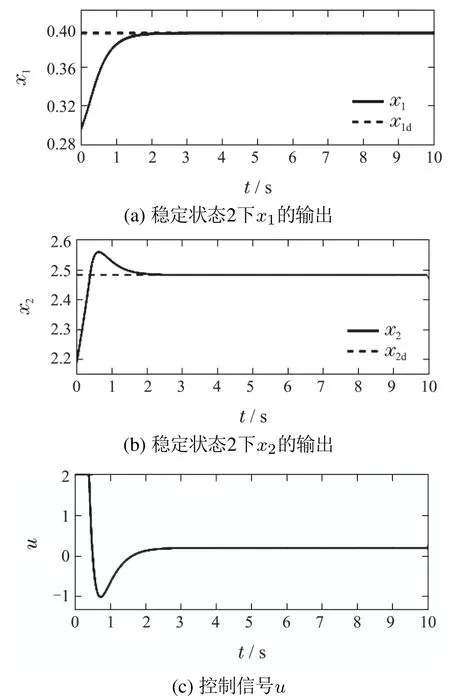
图3 稳定状态2仿真结果Fig.3 Simulation result of state 2

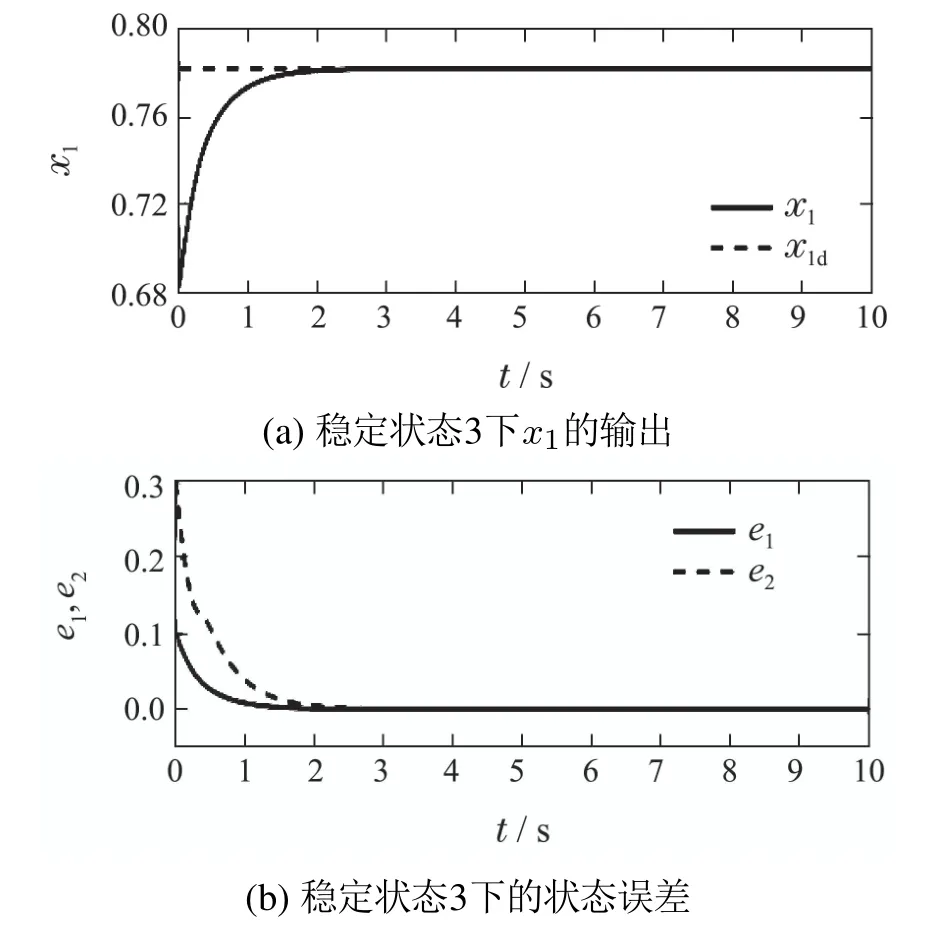
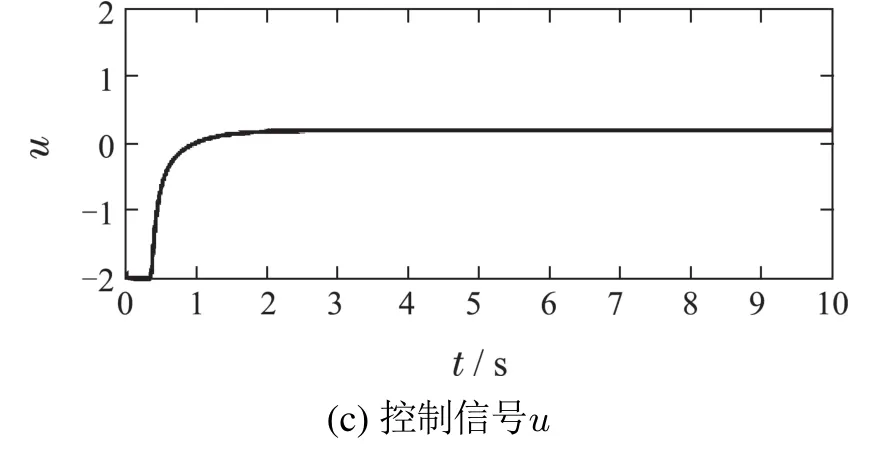
图4 稳定状态3仿真结果Fig.4 Simulation result of state 3

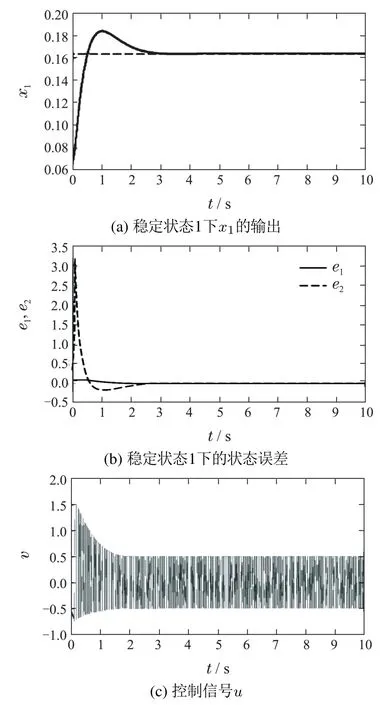
图5 文献[22]稳定状态1仿真结果Fig.5 Simulation result of steady state 1 in paper[22]

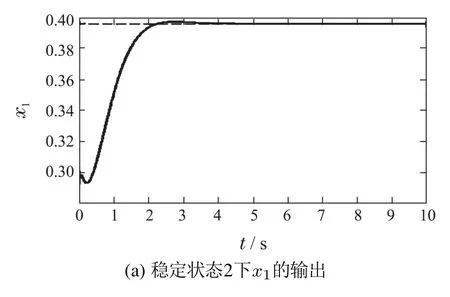
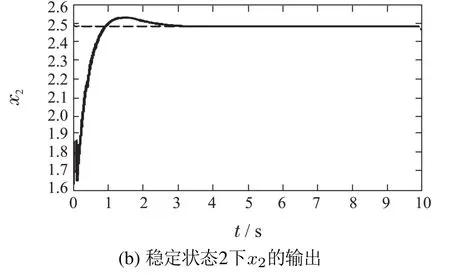
图6 文献[22]稳定状态2仿真结果Fig.6 Simulation result of steady state 2 in paper[22]

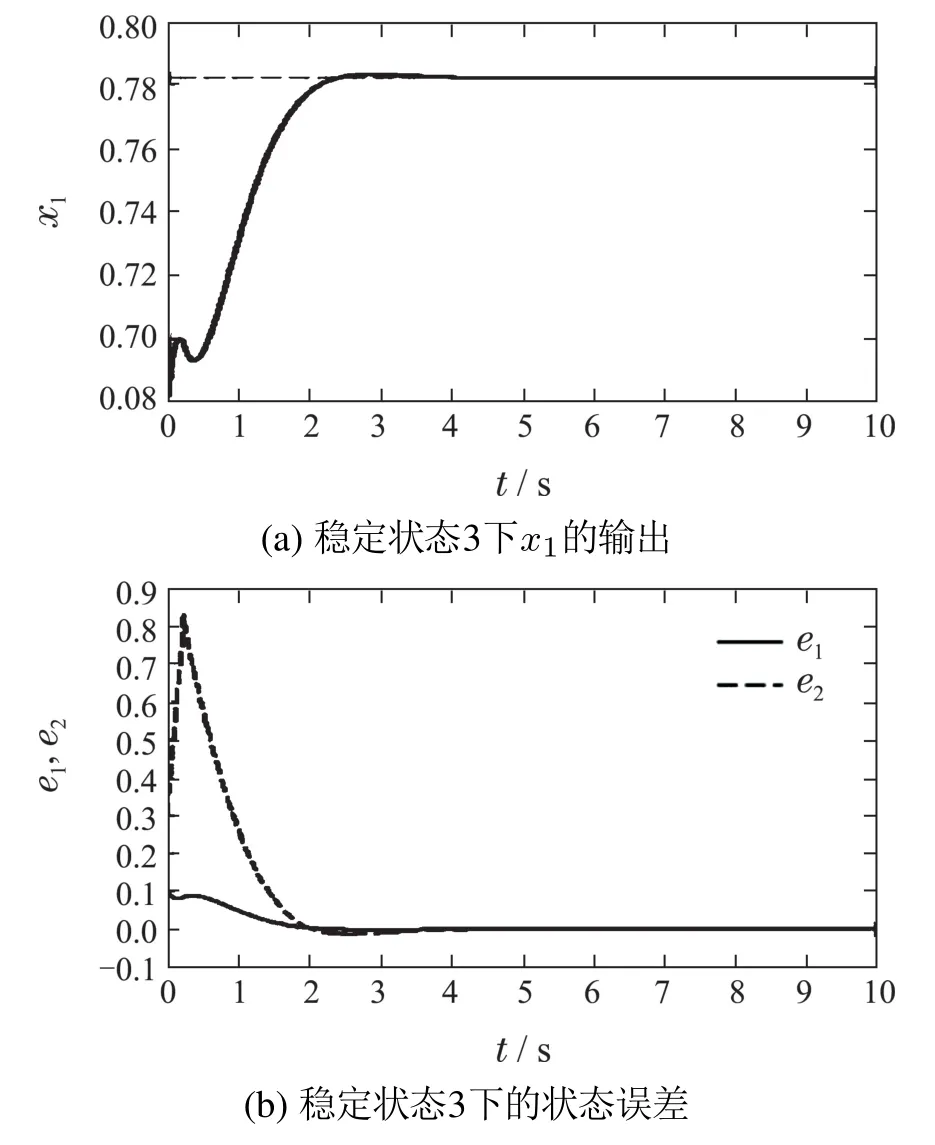
图7 文献[22]稳定状态3仿真结果Fig.7 Simulation result of steady state 3 in paper[22]

仿真结果表明,与文献[22]相比,本文的ACPID控制方法具有更好的动态品质:响应速度快、无超调、控制信号光滑.此外,ACPID状态调节器结构简单,仅涉及一个速度因子的镇定,而且速度因子在20 ≤zc≤100的范围内,ACPID控制方法都能获得良好的控制效果,因而便于实际应用;而文献[22]使用的滑模控制方法不仅结构复杂、计算量大,而且动态品质欠佳,控制信号存在高频抖振现象,容易破坏执行机构.

5 结论

针对一类非线性不确定CSTR系统,本文使用了一种ACPID控制方法,其主要特色在于:1)ACPID状态调节器结构简单、只涉及一个速度因子的镇定,便于实际应用;2)ACPID控制系统具有大范围鲁棒稳定性和良好的抗扰动鲁棒性.仿真结果表明:与文献[22]相比,本文的控制结果在动态品质与稳态性能方面都具有明显优势.