兼顾平顺性与车高调节的重型车空气悬架控制
孙维超 ,张晋华 ,潘惠惠
(1.哈尔滨工业大学航天学院 智能控制与系统研究所,黑龙江 哈尔滨 150001;2.广州大学 机械与电气工程学院,广东广州 510006)
1 引言
重型车指整车总质量大于3500 kg的M类(至少4个车轮、载客、机动)或N类(至少4个车轮、载货、机动)汽车[1].相比于轻型车辆,重型车由于其载重量的极大提升,可以更大限度地提高货物的运输效率.另一方面,由于空气悬架质量轻、刚度可调以及车身高度可调等一系列优点,在对车身高度调节及平顺性有要求的重型车辆中得到了广泛的应用.因此,对重型车空气悬架的平顺性及车高调节控制具有重要的意义.
空气悬架可以实现重型车的两个重要功能:一为平顺性能的提升;一为车身高度的调节.其中平顺性能是车辆悬架对路面冲击及车身振动衰减的考察指标,因此车辆悬架的控制目标即为降低车身垂向加速度,以此提高车辆的平顺性能[2–8].目前,对于空气悬架的平顺性能控制方法研究主要包括:PID控制、模糊控制、H∞控制、LQG(线性二次最优)、遗传算法等[9–11].在文献[12]中采用模糊控制方法对重型车空气悬架进行控制,以同时提高重型车的平顺性及道路友好性;文献[13]针对车辆电控空气悬架同时设计了H∞控制器以及LQG控制器,通过对比分析得出H∞控制器在悬架平顺性能提升方面的优势.以上所述控制方法,尽管其控制算法不同,对于空气悬架的控制原理都为通过对空气悬架进气排气电磁阀的控制实现对空气弹簧内部气压的控制,以此改变空气弹簧的作用力,实现缓冲减振功能,提高空气悬架系统的平顺性能.
空气悬架的另一个重要功能为车身高度调节控制,不同的车身高度可以适应不同的车辆行驶环境以及装载环境[14].文献[15]提出了电控空气悬架车身高度调节的神经网络PID控制方法,旨在实现车高调节控制的同时,实现整车姿态控制;文献[16]针对电控空气悬架在车高调节过程中出现的振荡问题,提出了模糊自适应方法,通过仿真表明其在车高调节过程中的有效性;孙晓强通过建立车高调节与整车姿态混杂系统动态模型,并以此设计车高调节与整车姿态混杂模型预测控制器,以此同时实现车高调节以及整车姿态控制问题[17].车高调节控制同样依赖于充放气电磁阀的通断控制,以此改变空气弹簧内气压,实现空气悬架的伸缩.
通过以上文献分析可以看出,目前的空气悬架车高调节控制追求精确性以及稳定性而忽略了控制过程中对平顺性能的影响;而在平顺性的控制过程中又不考虑对车高变化的影响.事实上,由于车辆平顺性以及车高调节都通过空气弹簧的充放气来实现,因此平顺性与车高调节的控制是彼此冲突与制约的,进而有必要同时考虑两者的控制问题.基于以上问题,考虑在车高调节的过程对车辆平顺性能的影响,本文提出了兼顾平顺性的空气悬架重型车车高调节鲁棒控制,以保证车高调节过程中的平顺性能.本文的创新点主要包括:1)提出了兼顾平顺性的空气悬架重型车车高调节控制策略,进而设计车身垂向加速度状态约束的车身高度跟踪控制器;2)在车高调节控制器的设计过程中考虑到未建模动态及外界干扰等不确定性,所设计的车高调节控制器具有一定的鲁棒性能.
本文后续章节结构安排为:在第2部分中,针对空气悬架物理模型建立相应的面向控制的动力学模型,并对控制问题进行描述;然后在第3部分中设计车身垂向加速度状态约束的空气悬架重型车车高调节鲁棒控制器;接着在第4部分中,通过仿真分析验证所提出的控制算法在保证平顺性能的同时对车高调节的控制效果;最后在第5部分得出相应的结论.
2 问题描述
建立空气悬架物理模型如图1所示,图中ms为簧载质量,mw为非簧载质量,cs为悬架减震器阻尼系数,kw为轮胎垂向刚度,cw为轮胎垂向阻尼,zs为簧载质量垂向位移,zw为非簧载质量垂向位移,zr为路面垂向输入,Q为流经电磁阀空气质量流量.
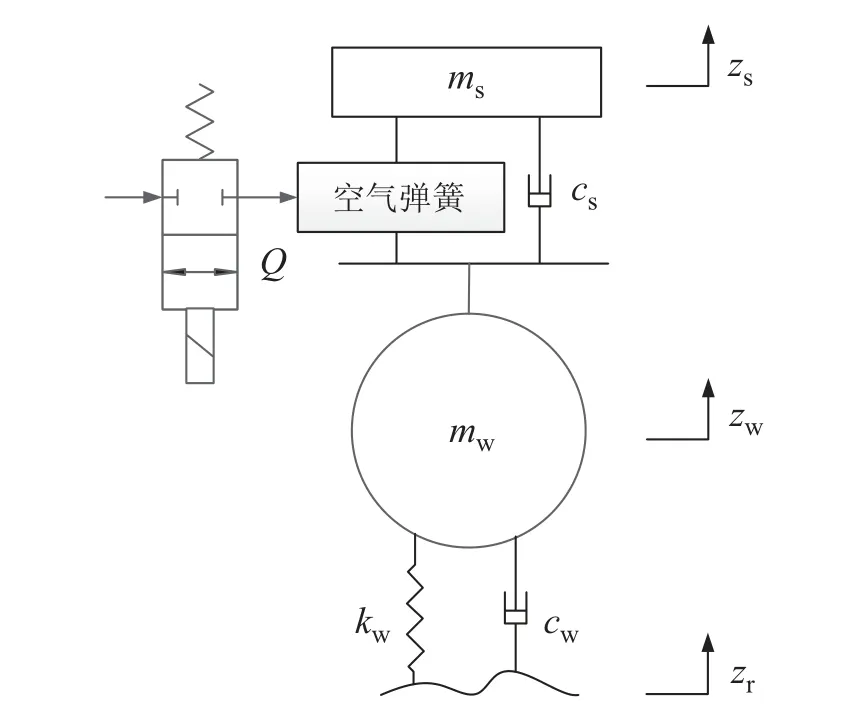
图1 空气悬架物理模型Fig.1 Physical model of air suspension
根据图1所示物理模型,建立面向控制的重型车车高调节动力学模型:簧载质量动力学模型为
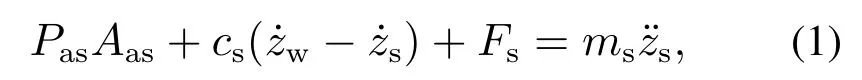
式中:Pas为空气弹簧腔压强,Aas为空气弹簧有效截面积,Fs为上界已知不确定性.其中zs为簧载质量垂向位移,表示车高调节被控量;其二阶导数为簧载质量垂向加速度,表示车辆平顺性被控量.显然车高调节与平顺性控制的控制对象都为簧载质量,但是其控制目标不一致:车高调节控制目标为簧载质量跟踪参考值,而平顺性控制目标为镇定簧载质量垂向加速度,因此两者存在制约与冲突.
非簧载质量动力学模型为
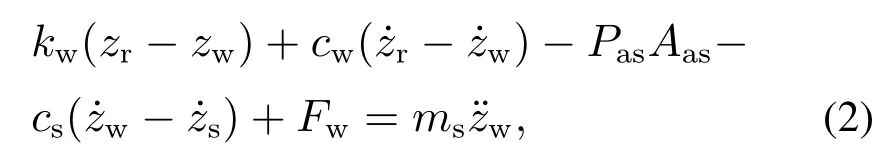
式中Fw为上界已知不确定性;空气弹簧气压腔气压动态模型为
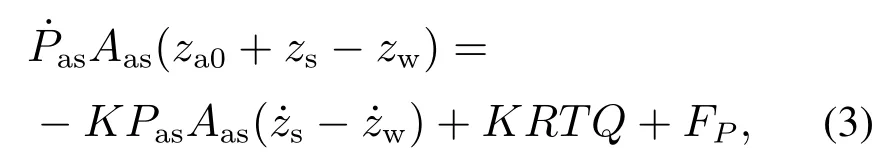
式中:za0为空气弹簧初始高度,K为多变指数,R为理想气体常数,T为气体温度,FP为上界已知不确定性.以上公式整理可得
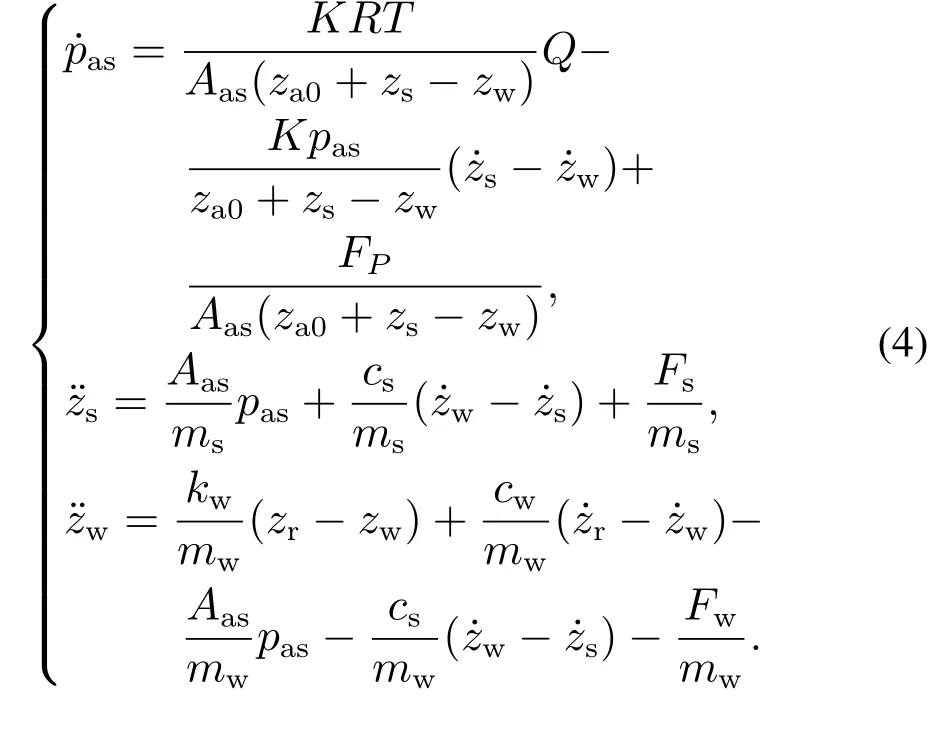
另一方面,根据GB/T 13442–92人体全身振动暴露的舒适性降低界限和评价准则中Z轴向(脚或臀部至头方向)振动加速度aZ的舒适性降低界限数值(表1)可知,当暴露时间一定,车身振动频率处于4∼8 Hz时,所要求的车身垂向振动加速度限值最严格;且当暴露时间为24 h时,车身垂向振动加速度限值最小,为0.04 m/s2.因此,在车高调节过程中,为保证整车平顺性,可以参考表1确定车身垂向加速度限值.
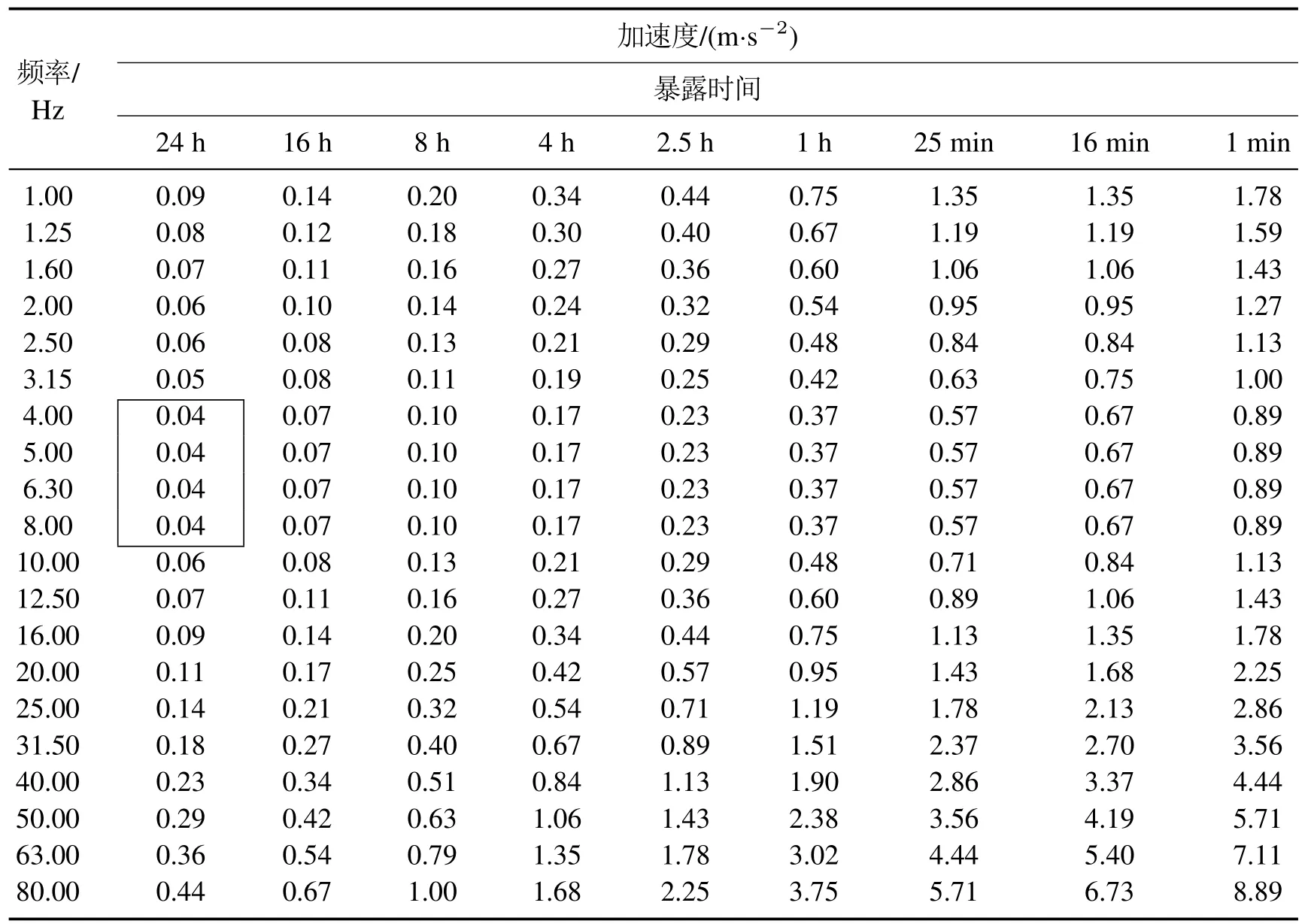
表1 Z轴向(脚或臀部至头方向)振动加速度aZ的舒适性降低界限数值Table 1 The comfort reduction limit value of vibration acceleration aZ in the Z-axis(foot or hip to head direction)
基于以上分析,控制问题可以描述为:设计控制器Q,使得zs跟踪到其参考值zsr,且在跟踪过程中保证车身加速度不超过其所要求的最大限值.
3 控制器设计
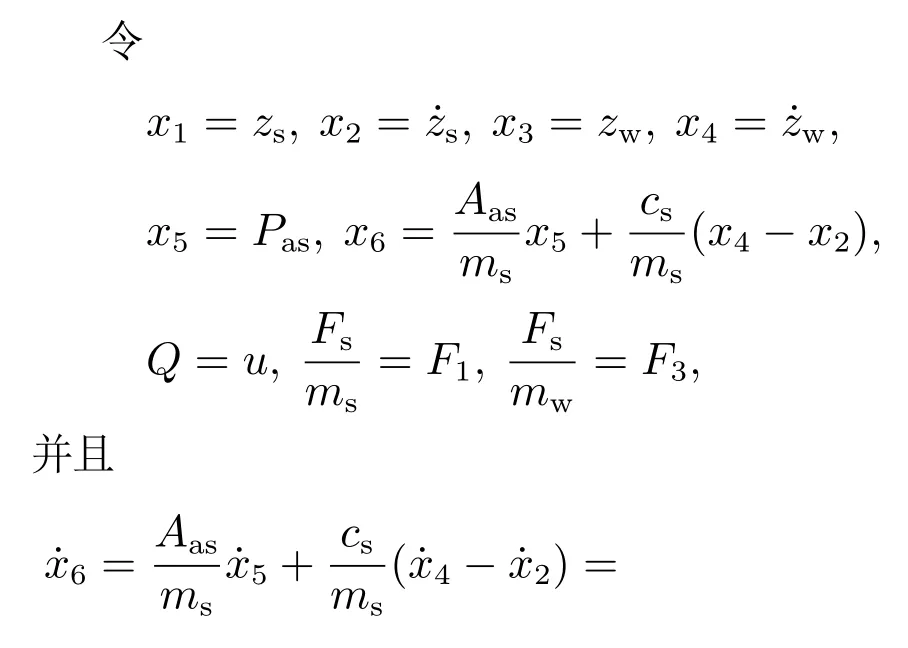

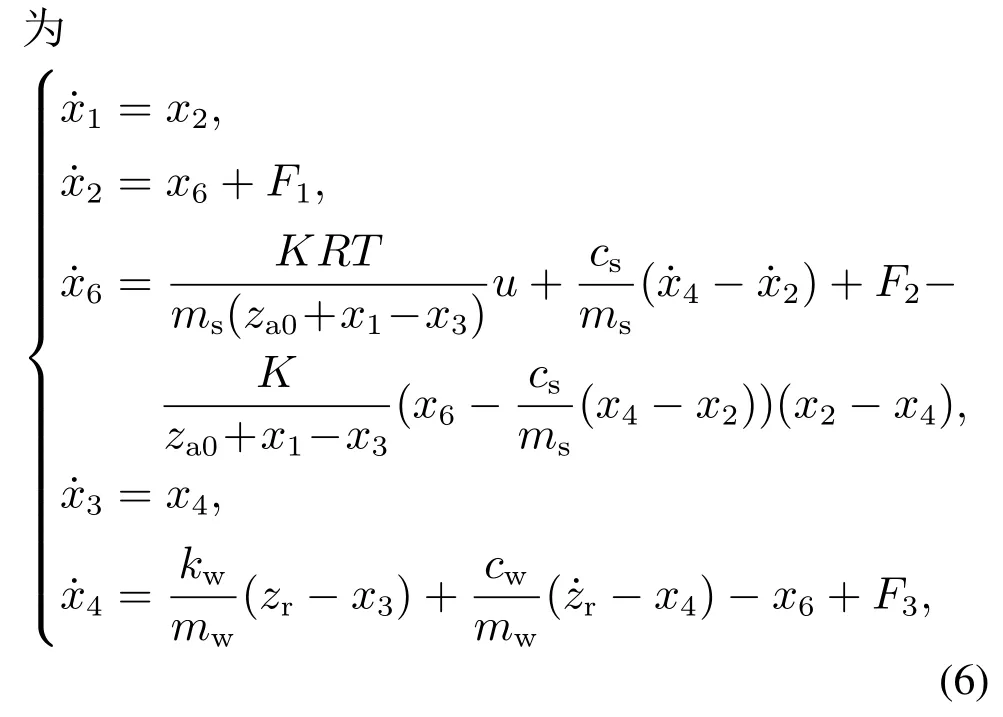
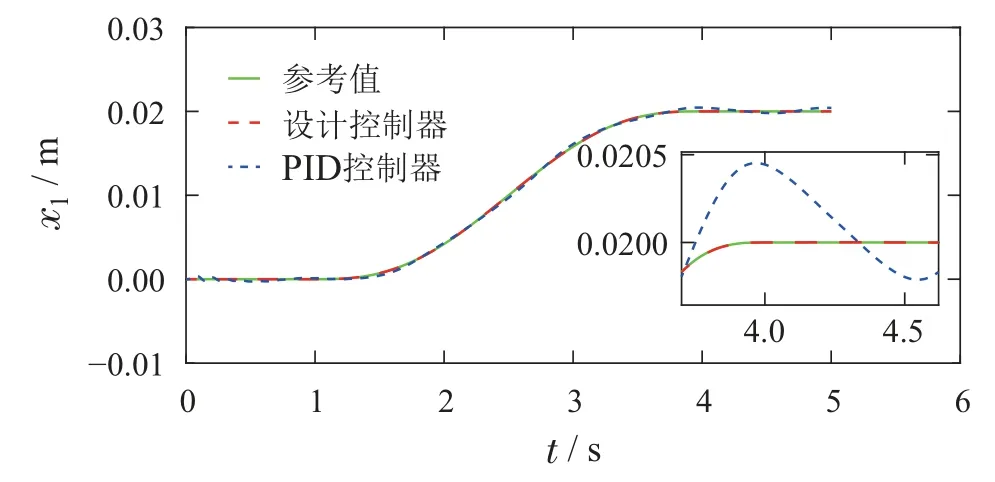
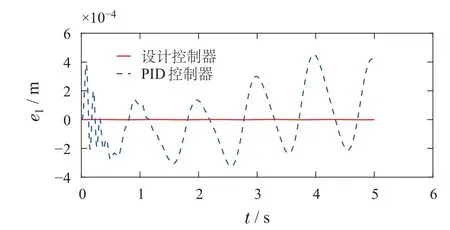
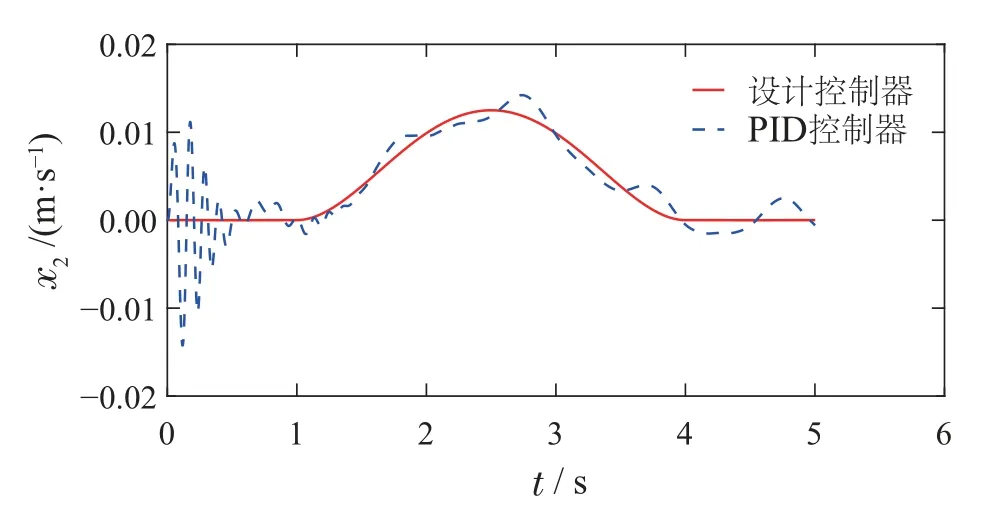
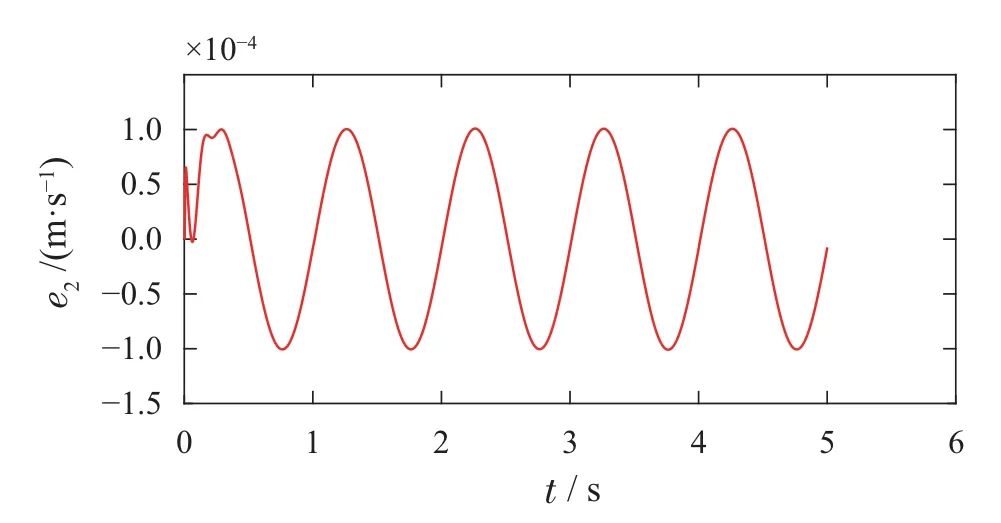
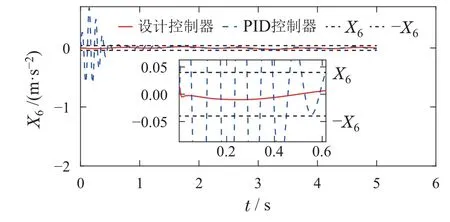
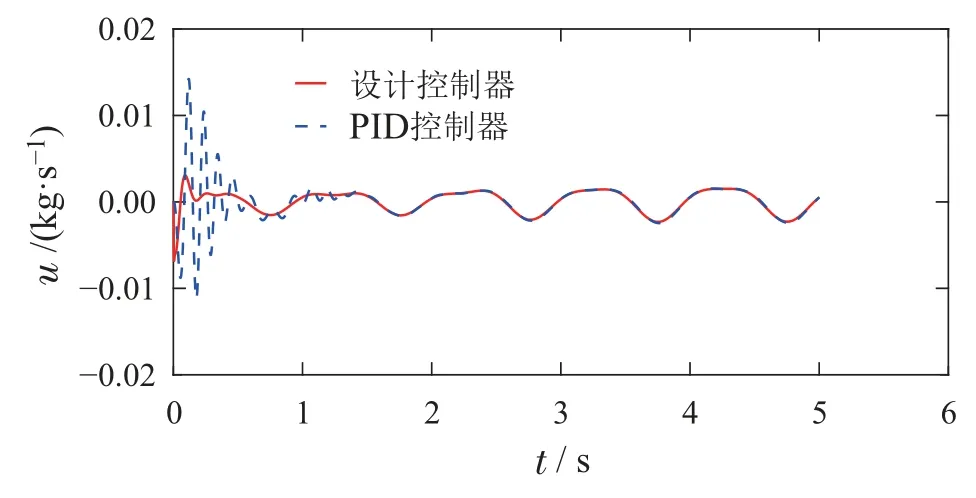
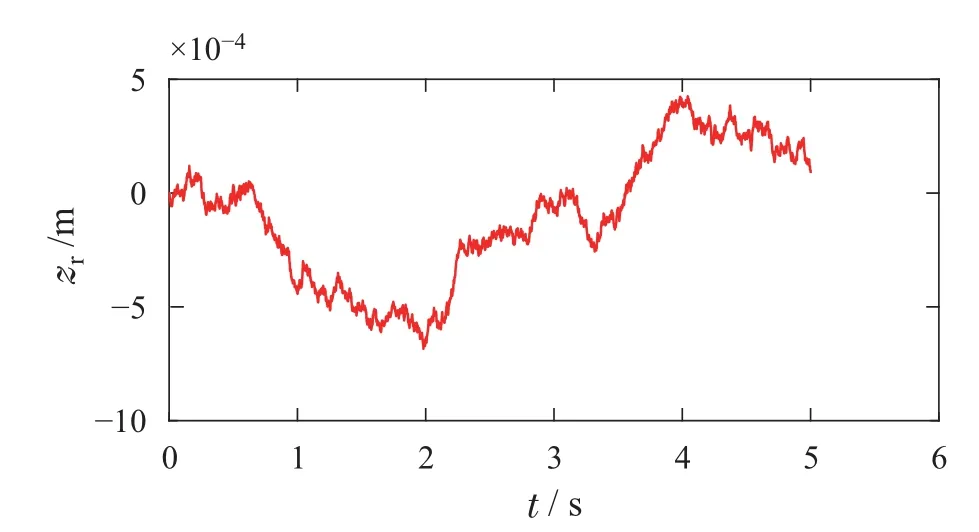
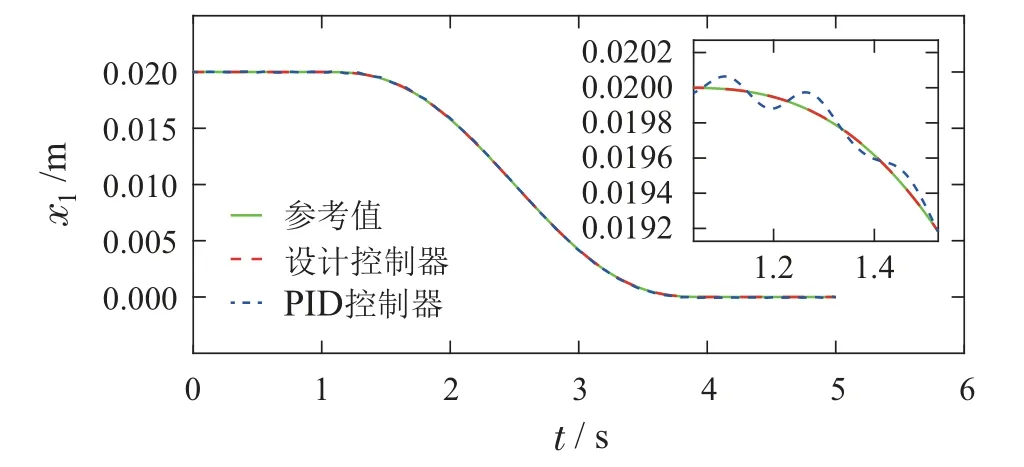
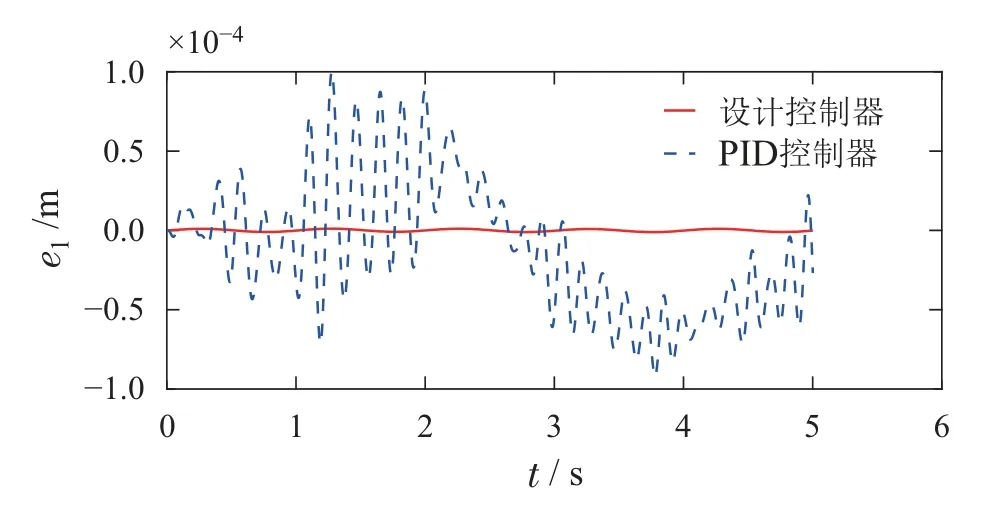
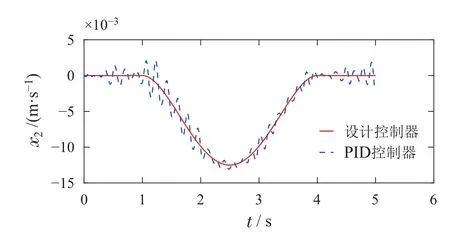
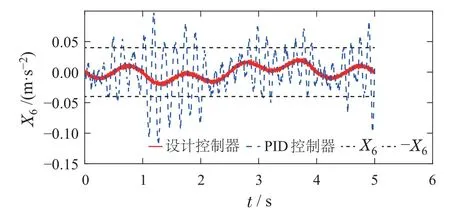
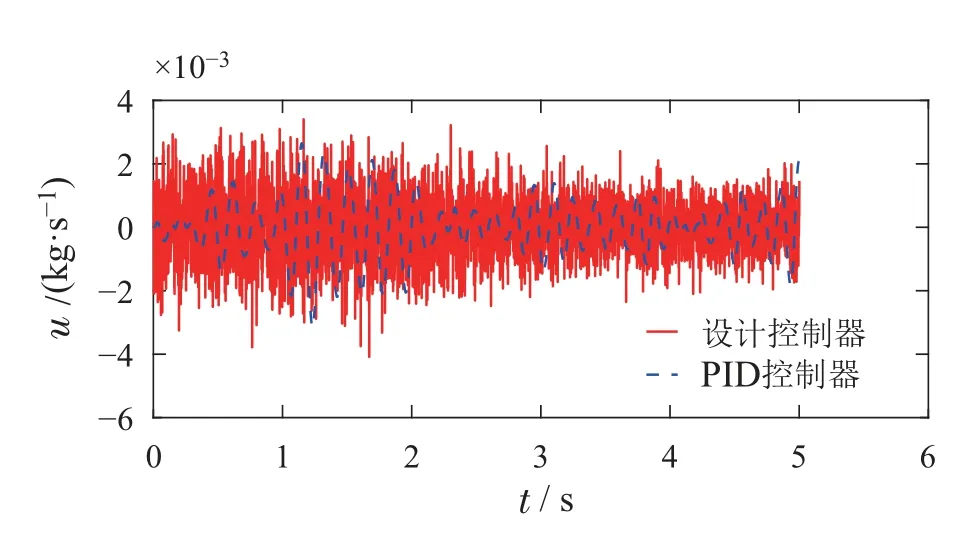
则控制目标可以进一步表述为:设计控制器u,使得|x6(t)| 控制器设计分为以下4个步骤. 步骤1令e1=x1−x1r,e2=x2−x2r,其中x2r为虚拟控制输入,则可以得到车高跟踪误差动态为 为保证车高调节前后整车平顺性,可以令h3=h6=0,h2与h4可以根据参考信号确定. 为验证所提出的兼顾平顺性的空气悬架重型车车高调节控制算法的有效性,进行仿真验证.仿真中车辆参数如下表2所示[18],控制器参数如表3所示.为验证说明所提出算法在车高调节过程纵平顺性方面的优势,同时对比地对采用PID控制算法 表2 1/4车辆参数Table 2 Quarter vehicle parameters 进行仿真,其中PID控制器参数同样列入表3中. 表3 控制器设计参数Table 3 Controller parameters 在正弦激励路面仿真过程中,参数设置如下:车辆在zr(t)=0.01 sin(2πt)的路面垂向输入下对车高进行调节,初始车高h1=0,目标车高h4=0.02,车高调节开始时刻T1=1 s,车高调节结束时刻T2=4 s,空气弹簧初始高度za0=0.03 m,簧载质量加速度限值X6=0.04 m/s2.不确定性外界扰动输入为F1(t)=F2(t)=F3(t)=0.01 sin(2πt);所有状态初始化为0,采样时间为0.001 s. 仿真结果如图2–7所示,图例中“设计控制器”表示所提出的兼顾平顺性的车高调节控制算法,“PID控制器”表示控制效果对比的PID控制器.图2为车高调节过程中车身高度对参考轨迹的跟踪效果,图例中“参考值”表示由式(38)与式(39)确定的参考车高调节曲线,在3 s内将车高由原始高度提高0.02 m;图3为相应的跟踪误差曲线.由图2及图3可以看出相比于PID控制算法,在提出的兼顾平顺性的车高调节控制算法可以以更小的误差实现对参考车高调节曲线的跟踪.同时注意到,在仿真过程中加入扰动项F1(t)与F2(t),仍然不会影响对参考车高的跟踪误差收敛效果,因此所提出的车高调节算法具有一定的鲁棒性. 图2 车身高度状态曲线Fig.2 State curves for the vehicle body height 图3 车身高度跟踪误差状态曲线Fig.3 State curves for the vehicle body height tracking error 图4表示在车高调节过程中车身速度状态曲线,其中在所提出的控制算法下对应的系统状态误差e2见图5.可以看出在在所提出的控制算法下,车身以更为光滑的曲线完成车高调节,然而在PID控制器作用下,车身速度在调节开始阶段展现出相当剧烈的抖动,影响车辆的平顺性. 图4 车身速度状态曲线Fig.4 State curves for the vehicle body velocity 图5 e2状态曲线Fig.5 State curves for the e2 车高调节过程中,车身加速度曲线如图7所示.图6中黑色虚线X6为在控制器设计过程中所要求的舒适性界限的加速度限值,本文中为X6=0.04 m/s2.从图中加速度曲线可以看出,在提出的兼顾平顺性车高调节控制器作用下,车身加速度被限制在0.04与−0.04之间;而在PID车高调节控制器的作用下,其车身加速度值远远超过X6,由此造成极差的整车平顺性能,即PID车高调节控制器无法对整车平顺性进行兼顾. 图6 车身加速度状态曲线Fig.6 State curves for the vehicle body acceleration 图7表示车高调节过程中控制输入曲线,即流经车辆悬架电磁阀空气质量流量.由图可以看出,在控制初始阶段,PID控制器所需要的控制能量远远大于所提出的兼顾平顺性的车高调节控制器,在控制后期,二者趋于相同. 图7 控制输入曲线Fig.7 Curves for the control input 为进一步通过数值直观地展示所提出车高调节算法的优势,表4列出了相应的性能指标,即车高跟踪误差与车身加速度均方根值(下标为rms).从表4中可以直观地看出所提出的兼顾平顺性的车高调节控制器相比与PID控制器可以同时提高车高跟踪性能与平顺性能. 表4 车高调节性能指标(正弦激励x路面)Table 4 Performance indices for height regulation(Sinusoidal excitation road surface) 在随机激励路面仿真过程中,路面垂向输入为滤波白噪声 其中:n1为下截止频率,v为车速,n0为空间参考频率,Gq(n0)为路面不平度系数.仿真中采用A级不平度路 面:n0=0.1 m−1,Gq(n0)=16×10−6m3,n1=0.01 m−1,v=10 m/s,如图8所示. 图8 A级不平度路面垂向输入Fig.8 Vertical input for A-class rough road surface 仿真过程中其他参数设置如下:初始车高h1=0.02,目标车高h4=0,车高调节开始时刻T1=1 s,车高调节结束时刻T2=4 s,空气弹簧初始高度za0=0.03 m,簧载质量加速度限值X6=0.04 m/s2.不确定性外界扰动输入为 所有状态初始化为0,采样时间为0.001 s. 仿真结果如图9–14所示.图9为车高调节过程中车身高度对参考轨迹的跟踪效果,在3 s内将车高由0.02 m的高度下降为0 m;图10为相应的跟踪误差曲线.同样由图9与图10 可以看出所设计的兼顾平顺性的车高调节控制算法相比于PID控制算法可以以更小的跟踪误差实现对参考车高调节曲线的跟踪.同时由扰动项F1(t)与F2(t)的存在可以证明所提出的车高调节算法具有一定的鲁棒性. 图9 车身高度状态曲线Fig.9 State curves for the vehicle body height 图10 车身高度跟踪误差状态曲线Fig.10 State curves for the vehicle body height tracking error 图11表示在车高调节过程中车身速度状态随时间变化曲线.根据图11同样可以看出在所提出的控制算法下,车身以更光滑的速度完成车高调节,然而在PID控制器作用下,车身速度在整个车高调节过程中都展现出相当剧烈的抖动,而影响车辆的平顺性能. 图11 车身速度状态曲线Fig.11 State curves for the vehicle body velocity 车高调节过程中,车身垂向加速度曲线如图12所示.图12中黑色虚线X6同样为在控制器设计过程中所要求的舒适性界限的加速度限值.从图中可以看出,在兼顾平顺性车高调节控制器作用下,车身加速度被限制在0.04与−0.04之间;而在PID车高调节控制器的作用下,其车身加速度值超过X6,整车平顺性能因此会降低,即PID车高调节控制器无法对整车平顺性进行兼顾. 图12 车身加速度状态曲线Fig.12 State curves for the vehicle body acceleration 图13表示车高调节过程中控制输入曲线,可以看出,所提出的兼顾平顺性的车高调节控制器所需要的控制能量要大于PID控制器. 图13 控制输入曲线Fig.13 Curves for the control input 同样在表5中列出了相应的车高跟踪误差与车身加速度均方根值性能指标.从表5中可以看出所提出的兼顾平顺性的车高调节控制器相比与PID控制器在兼顾车高调节性能与平顺性能方面的优势. 表5 车高调节性能指标(随机激励路面)Table 5 Performance indices for height regulation(Random excitation road surface) 通过以上正弦激励路面与随机激励路路面仿真可以得出,在所提出的兼顾整车平顺性的车高调节控制器作用下,车身高度可以在加速度约束的调节下,实现对目标车高轨迹的跟踪;而在PID车高调节控制器作用下,会造成很大的车身加速度值,进而极大降低整车在车高调节过程中的平顺性.另外相比于PID车高调节控制器,本文提出的兼顾整车平顺性的车高调节控制器可以以较小的跟踪误差实现对参考车高曲线的跟踪. 本文提出一种兼顾平顺性的空气悬架重型车车高调节鲁棒控制算法,所设计的车高调节控制算法可以在加速度限值范围内实现对参考车高曲线的跟踪,并且对外界扰动具有一定的鲁棒性.另外,相比于PID车高调节控制,所提出的兼顾平顺性的空气悬架重型车车高调节鲁棒控制算法能够以更小的跟踪误差、车身加速度实现车车高调节,体现出更优的控制效果.论文中采用数值仿真的形式对所设计车高调节控制器算法进行验证,在后续的研究过程中将进一步采用CarSim仿真验证以及台架实验验证.



4 仿真分析

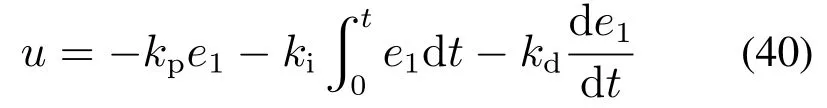

4.1 正弦激励路面

4.2 随机激励路面
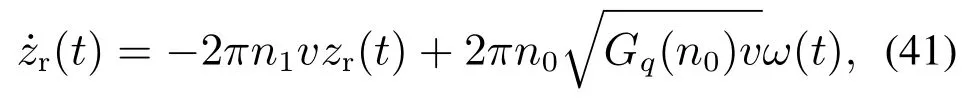
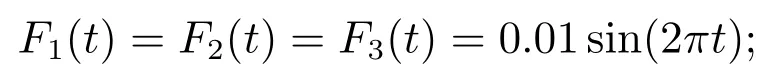

5 结论

