改进的广义Feistel结构轻量级分组密码算法

张晓枫,刘永桂

(华南理工大学自动化科学与工程学院,广东广州 510641)

1 引言

随着物联网的兴起和蓬勃发展,世界进入万物互联时代;通信、计算机等信息技术得到快速发展,传统工业系统+互联网,形成了集传感、控制、网络和计算一体的信息物理系统.随着信息物理系统与网络联系越发紧密,信息安全问题愈发突出.密码学作为信息安全技术的核心与基础,是信息安全的重要研究方向之一.

信息物理系统设备类型多样,设备资源和计算能力不足,常用的密码学算法计算量大、硬件实现复杂等,并不适用.分组密码算法一直是研究的热点,许多密码学者在轻量级密码学上进行了深入研究[1–2],提出了一些优秀的算法,如:DESL[3]、轻量级AES[4]、PRESENT[5]和SKINNY[6]等,推动了轻量级分组密码算法的研究和发展.PRESENT算法由于其安全与高效性等优点,成为了轻量级分组密码算法的一个标杆.文献[7]提出轻量级分组密码算法在某种程度上缺乏灵活性,它们一般针对特定的平台(如ASIC),在此类平台下设计的算法通常具有较好的性能,但移植到别的平台下表现却一般,如:资源占用率高、软件实现效率低、缺乏灵活性等.

轻量级分组密码算法的基本数学模型如图1所示.

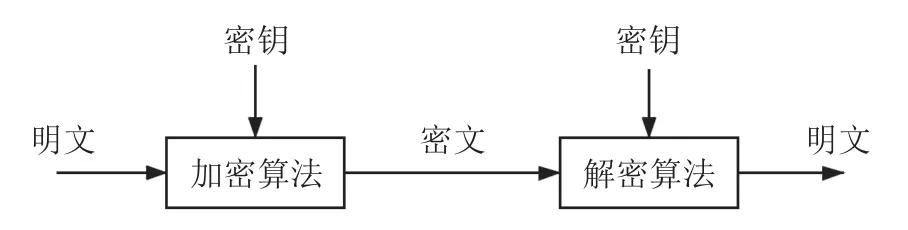
图1 分组密码算法的数学模型Fig.1 Mathematical model of block cipher algorithm

2 相关知识介绍

2.1 符号及术语说明

本文所采用的符号及说明如表1所示.

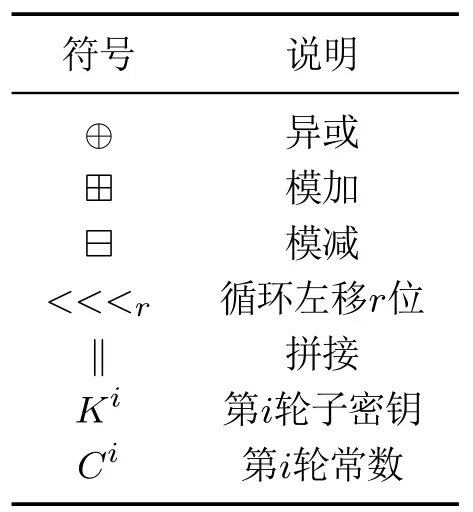
表1 所用的符号说明Table 1 Symbols in paper

2.2 常用分组密码结构介绍

在分组密码学中,主流算法主要采用了SPN结构、Lai–Massey结构(L–M结构)、Feistel结构和广义Feistel结构等[8].SPN结构具有良好的混淆和扩散性,且基于SPN的算法实现流程较短,因而受到广泛的关注,但该类算法的缺点是结构不对称,需要分别设计加密和解密算法;L–M结构主要起源于国际数据加密标准算法IDEA,是在1999年由Vaudenay研究IDEA算法中结构的一般性所提出来的密码结构模型[9].L–M结构算法混淆和扩散很快,并且加密和解密一致,但其轮函数设计比较复杂,在硬件上实现时需要使用更多的门电路;基于Feistel结构的分组密码结构简单,具有对称性,软硬件较易实现,并且不需要特别地设计其解密函数,这样就使得其在硬件实现上可以省去一半的设计,但基于Feistel结构的算法混淆和扩散速度较为缓慢,每次只能处理一半的数据;而广义Feistel结构是对Feistel结构的扩展,其混淆和扩散速度得到了一定的提升,加之其具有对称性,在软件实现上较快,硬件实现上可减少资源.这就使得基于广义Feistel结构的分组密码算法在资源紧张的信息物理系统中具有很大的优势,本文将采用广义Feistel结构来实现分组密码算法.

Feistel结构和广义Feistel结构如图2所示.

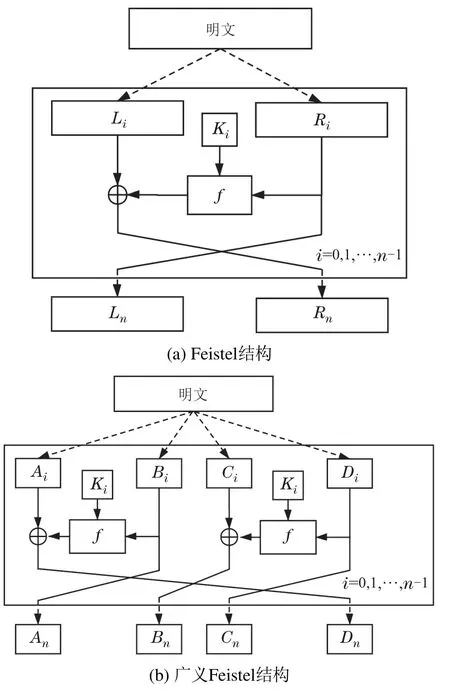
图2 经典Feistel结构和广义Feistel结构Fig.2 Feistel structure and generalized Feistel structure

经典的Feistel结构(如图2(a)),其将明文分成左右两个部分Li和Ri,每轮通过轮函数f将明文进行混淆和扩散,但每轮只能处理一半的数据.广义Feistel结构将明文分成多份,如图2(b)所示;广义Feistel结构密码算法可以表示为

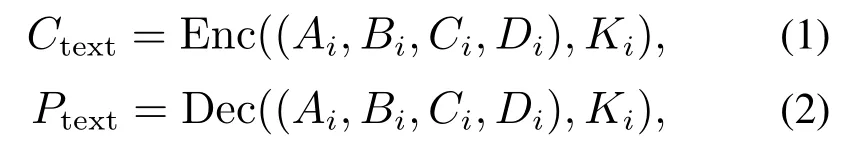
其中:Ctext是密文,Ptext是明文,Ki是每轮子密钥,Ai,Bi,Ci,Di是加密/解密中明文的轮状态,加密时i从0∼n −1,解密时从n∼1.

3 GFARX算法设计及实现

3.1 GFARX算法设计

经上述分析,Feistel结构可以减少一半的软硬件设计,这对于资源有限的信息物理系统来说具有很大优势;而广义Feistel结构又弥补了Feistel结构混淆和扩散速度慢的不足,这使得广义Feistel结构成为本文设计轻量级分组密码算法(generalized Feistel structure based on ARX structure,GFARX)的首选.

目前,无论是基于SPN结构、Feistel结构还是广义Feistel结构的算法,大多采用S盒来进行非线性替换(substitution)和P盒来进行线性置换(permutation),以保证算法的混淆性和扩散性.一般采用8×8的非线性S盒与P盒来对算法进行混淆和扩散,导致了算法轮函数的计算量较大;虽许多学者在S盒与P盒上进行轻量化的研究,如PFP[10]算法仅采用4×4的S盒与P盒;其使用到G(28)上的模乘运算,该运算复杂且耗费较大的计算资源;并不适用于资源受限的信息物理系统.因此,如何脱离模乘运算也是轻量化算法的一种思路.

ARX结构是由模加、循环位移和异或操作组合而成的一种密码学结构[11].相较于S盒与P盒,ARX结构更为简单;其非线性部件是模加运算,在软硬件上实现简单,但其循环位移和异或运算则保证了算法的扩散性[12].虽然ARX结构简单,但经过算法的多轮迭代,其包含的3种操作却又给算法带来了非线性和复杂性.这使得ARX结构在快速实现分组密码算法上有很大的优势.

本算法采用了ARX结构替换广义Feistel结构中的S盒与P盒,使得新设计的分组密码算法在软硬件上的实现更加快速,同时也保证了其混淆性和扩散性.本文所设计的分组密码算法结构(GFARX)如图3所示.

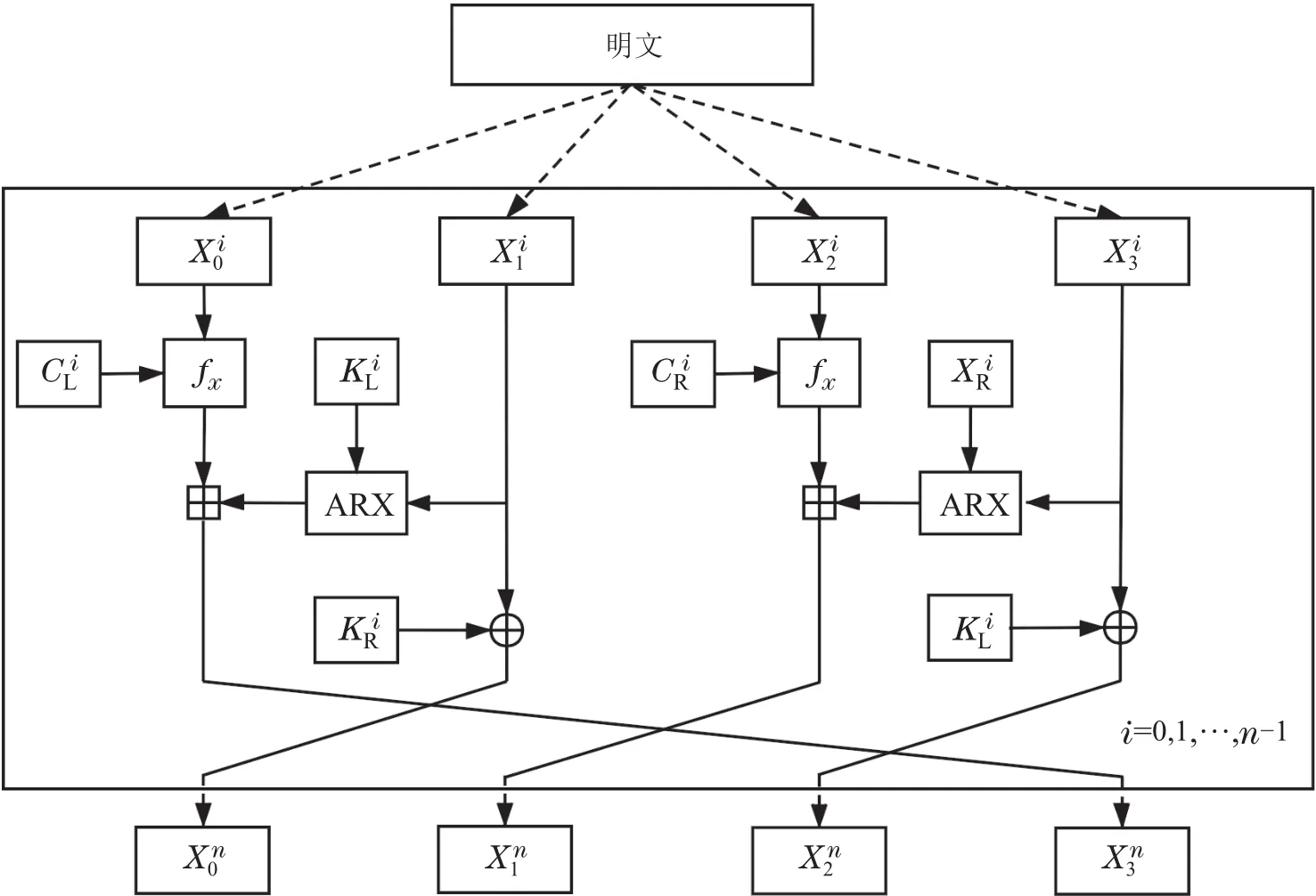
图3 GFARX结构Fig.3 GFARX structure

从图3中看出,本文所设计的GF–ARX结构将明文分成了4个部分,即M=X0∥X1∥X2∥X3.GFARX算法和基于广义Feistel结构的分组密码算法一样,结构对称,加密算法和解密算法相似,不必特别地设计解密算法,只是加密和解密顺序相反,按反循序使用子密钥进行解密即可.

从图2(a)与图2(b)对比可以看出,广义Feistel的4分支结构加快了算法的混淆和扩散速度;但其非线性部分(S盒)与线性部分(P盒)均在轮函数中,仅采用异或的手段处理奇数分支,导致了算法的混淆性和扩散性集中于一点,容易被破解.本文针对该不足,采取以下几种方式对广义的Feistel结构进行改进:

1) 将奇数分支的异或运算改成模加运算,增强算法的混淆能力;

2) 增加fx结构来增强奇数分支的扩散能力;

3) 采用非对称双子密钥处理中间状态,使得算法的所有分支都与密钥相关,不存在未处理的分支,以增强算法抵抗暴力分析的能力;

4) 设计了可修改的轮常数,以增加算法的灵活性和安全性.

算法中的ARX结构和fx函数设计如图4所示.

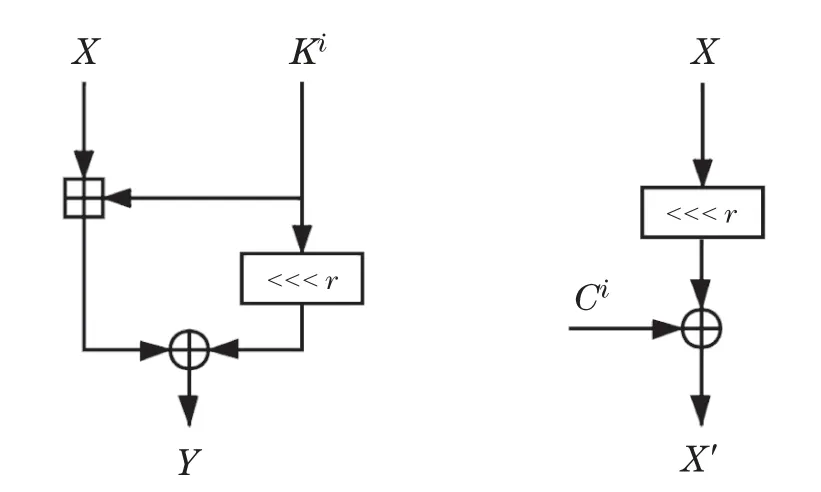
图4 ARX结构(左)和fx函数结构(右)Fig.4 ARX structure(left)and fx structure(right)

GFARX算法中的ARX结构和fx函数表示为

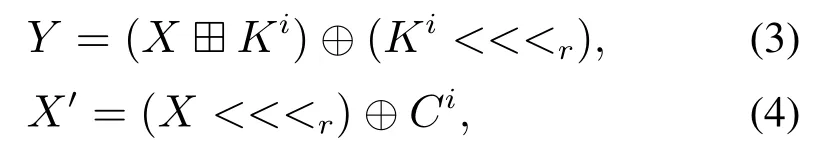
式(3)中Ki是第i轮子密钥,式(4)中Ci是第i轮常数.此外,可修改常数的设计原理是采用圆周率π和自然底数e的小数位,具体的设计为

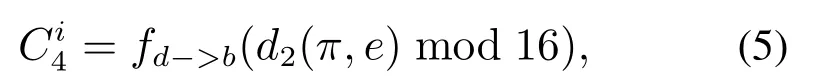
通过上述设计,解决了广义Feistel结构中的不足,增加了算法分析的复杂性和提升了算法的安全性,却只增加了少量计算量.

3.2 GFARX算法实现

GFARX算法提供了6个版本的分组密码算法,如GFARX–128/128,其中前面的数字代表明文的分组长度(比特数,记为BL),后者代表密钥的长度(比特数,记为KL).不同的BL适应不同位数的CPU,不同的KL代表不同的安全等级.可用的分组长度和密钥长度及其加密的迭代次数设计如表2所示.

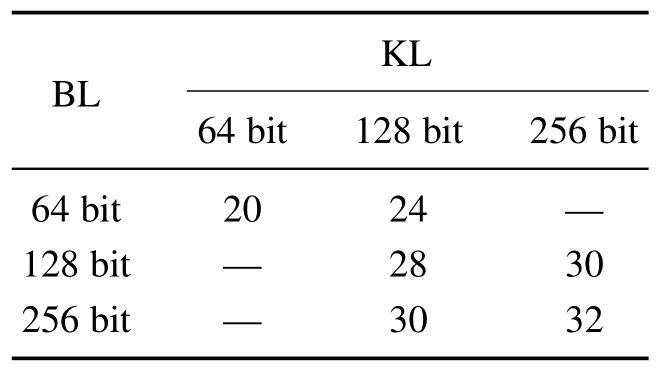
表2 GFARX算法不同版本的迭代次数Table 2 Number of iterations in different versions of the GFARX algorithm

BL和KL分别包含64,128和256三种长度,根据实际情况选择不同版本的分组密码算法,以满足安全性和计算性能的需求.

GFARX算法的加密/解密流程如图5所示.

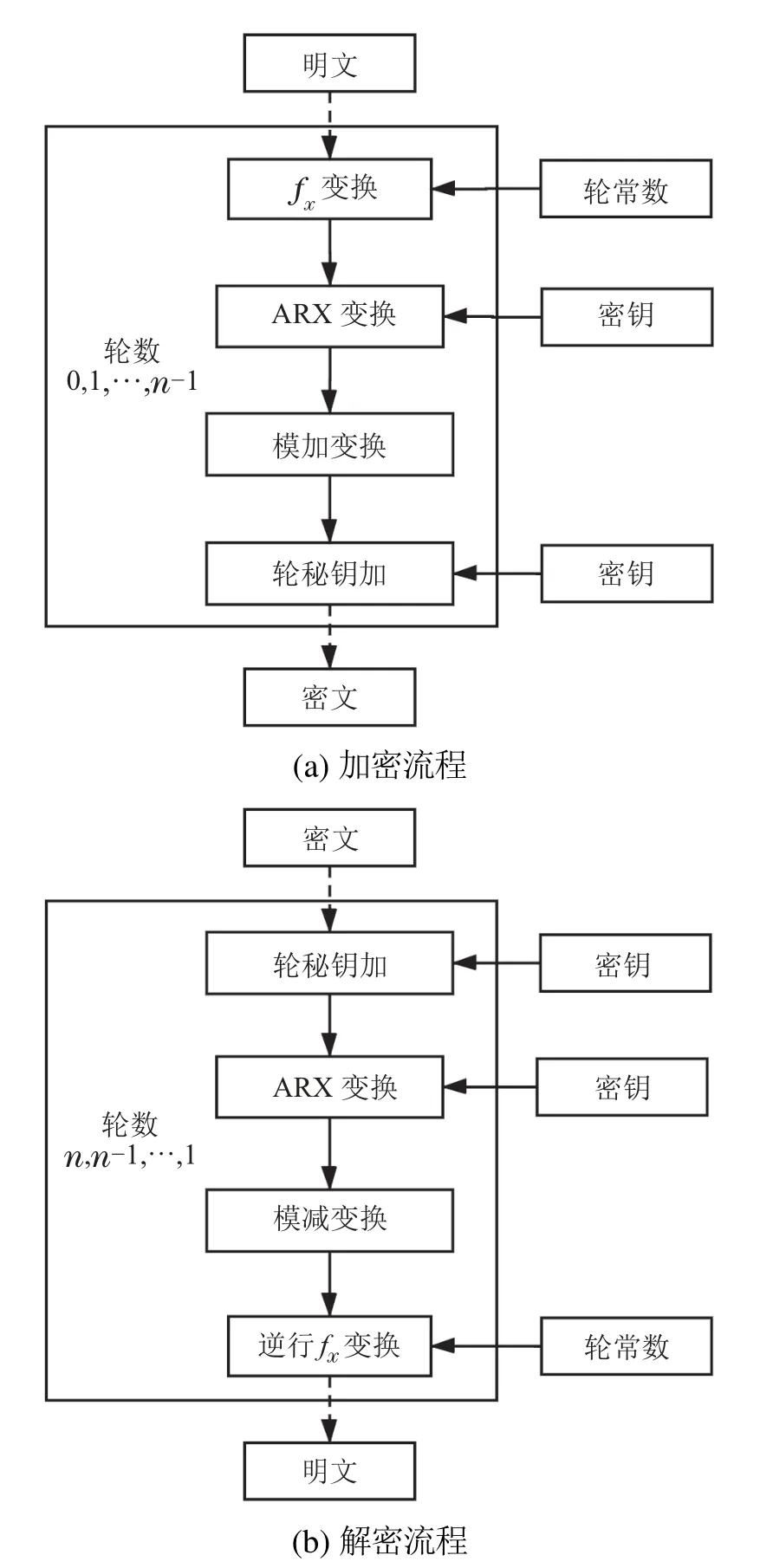
图5 加密流程和解密流程Fig.5 Encryption process and decryption process

加密流程和解密流程十分相似,只是加密流程和解密流程的顺序相反,并采用反顺序使用轮密钥来解密密文[13].但解密流程需将加密流程中的模加变换改为模减变换,并且fx变换要使用其逆变换.每轮中间状态X的迭代加密可用以下公式表示:

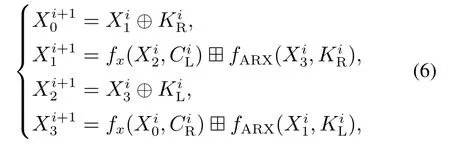
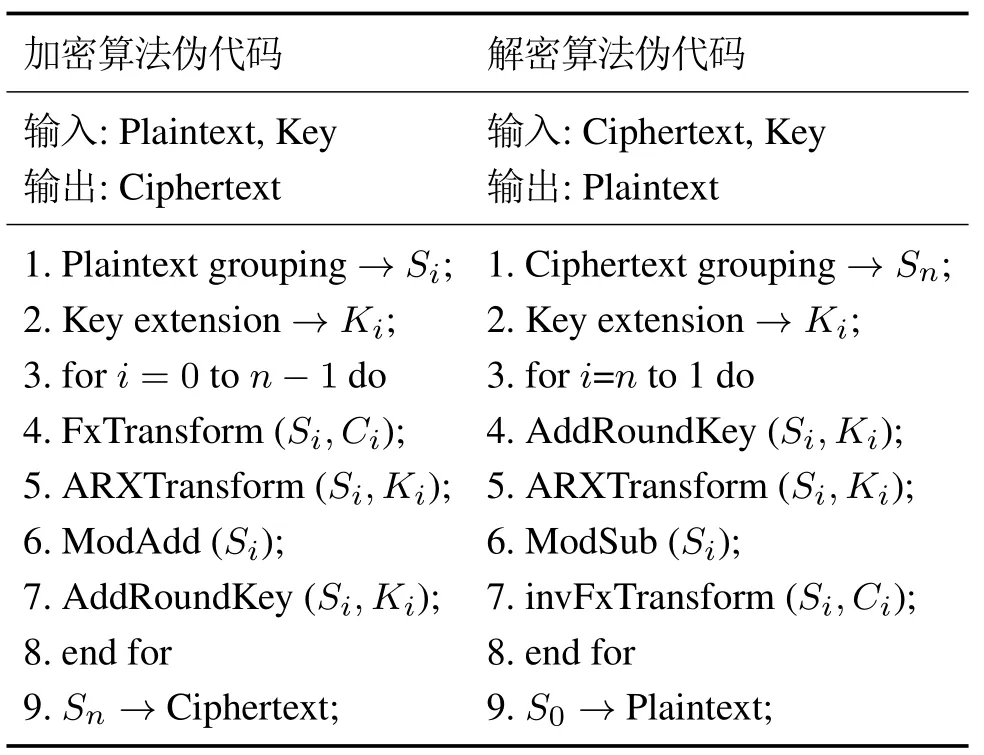
表3 加/解密算法的伪代码实现Table 3 Pseudocode of encryption/decryption algorithm

3.3 密钥扩展

由于密钥是64/128/256 bit,而每个版本的算法均有20轮以上的中间状态需要加密,因此需要对原始密钥进行扩展.假设主密钥K=k0∥k1∥k2∥k3,则密钥扩展算法可用如下公式表示:

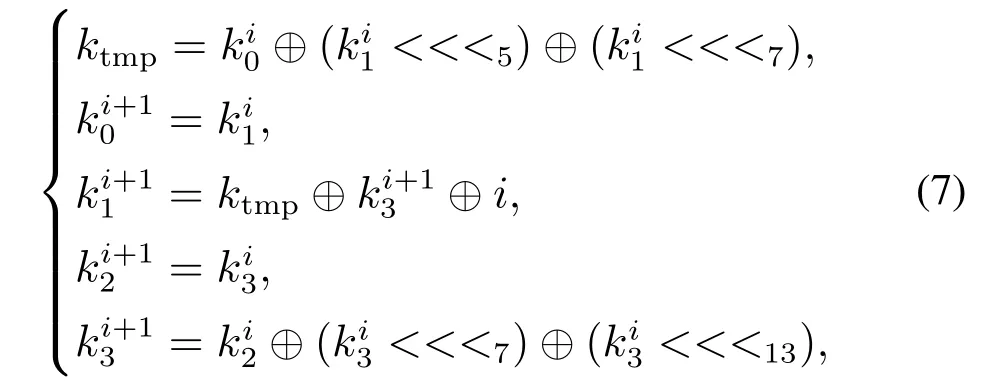
式(7)中ktmp是保存密钥的临时变量.密钥扩展算法的伪代码实现如表4所示.

表4 密钥扩展算法的伪代码实现Table 4 Pseudocode of key expansion

3.4 加密模式

分组密码算法将要加密的明文数据分成固定长度的数据块进行加密,常见的分组密码算法的工作模式有:ECB(电子密码本)模式、CBC(密码块链)模式、CFB(密码反馈)模式、OFB(输出反馈)模式和CTR(计数器)模式[14].ECB模式是最简单的加密模式,其将明文分成固定大小的数据块,每个数据块被单独加密,加/解密的方法一致,虽可并行计算,但其缺点是一旦有一个数据块被破解,其他的数据块可被同样破解,因而该模式安全性较差.

CBC模式是最常用的加密方式之一,其在每一个分组数据块加密前与前一个加密好的分组数据块进行XOR(异或操作),然后再进行加密.这样,每个密文数据块就依赖于其之前的所有明文分组数据块,即使破解了某个密文数据块,也很难通过同样的方法来破解其他的数据块,因而提升了算法的安全性.为保持数据块的一致性,需要在第一块明文数据块加密前使用初始化向量来对其进行异或操作.

4 算法分析

4.1 GFARX算法设计分析

在设计时,综合考虑了GFARX算法的安全性、软件性能和硬件实现代价,将ARX结构融合于广义Feistel结构中.广义Feistel结构加快了明文的混淆和扩散速度,采用模加替换了传统的非线性S盒,相较于S盒操作,模加操作更加快速,易于软硬件实现.在轮数设计时,采用ARX结构来尽可能轻量化分组密码算法的实现.同时模加、循环位移和异或组合带来的复杂性也提高了算法的安全性.

4.2 算法整体结构分析

SPN、Lai–Massey和Feistel结构是常用的分组密码算法结构,一般算法多基于SPN结构和Feistel结构.SPN结构虽然混淆和扩散速度快,算法设计所需轮数较少,吞吐量较大,但其加密和解密算法不一致;Lai–Massey结构的混淆和扩散速度较快,但轮函数设计较为复杂,硬件实现占用资源较多;而广义Feistel结构对称,实现简单,不需要特别设计解密算法.本文设计的4分支广义Feistel结构算法可以有效地减少组件大小,增加组件的个数,从而提升了算法设计的灵活性和可扩展性,有利于轮函数中的各组件进行并行运算,加快运算速度.

4.3 ARX结构与S盒+P盒分析

ARX结构中使用模加、循环位移和异或操作替代经典分组密码算法中的非线性S盒和线性变换P盒.模加操作的当前比特位与所有比当前位低的比特位相关,当前位的更高位由于只与进位相关,因此低位混淆速度快而高位混淆速度慢,混淆程度是低位均匀而高位不均匀.但ARX结构中的模加配合循环位移,只需将循环位移的位移参数设计得合理,即可加快高位的混淆速度,达到高低位混淆均匀的目的.此外,模加、循环位移和异或操作相较于S盒与P盒操作有更快的运算速度和更简单的硬件实现,这对于受资源限制的信息物理系统来说十分重要.

4.4 算法的安全性分析

密码算法的差分分析[15]和线性分析[16]是针对分组密码算法的有效攻击手段,文献[15–16]详细论述了评估密码算法抗差分和线性分析的实际方法.下面给出了密码算法的整体安全性分析和抗差分能力分析与抗线性能力分析.

4.4.1 算法整体结构安全性分析

GFARX算法整体采用广义Feistel结构,而广义Feistel结构在分组密码算法中已经得到了广泛的应用,具有良好的结构安全性.可证明:在fARX函数是伪随机的假设下,3轮的广义Feistel结构是伪随机的.算法中每轮有4处模加操作,除ARX结构外,广义Feistel结构的奇数分支也采用了模加运算,以提升算法的非线性混淆能力,因此加大了分析算法的复杂性,从而提升了算法的安全性.

轮常数在本文提供了默认的设计方案,在实际应用中可根据使用情况设计新的轮常数.轮常数的可动态修改,相当于轮常数的设计会随着使用者的改变而改变,提升了算法的安全性;若所设计的轮常数从未公开,则任何的密码分析均不可能奏效.

4.4.2 差分分析

GFARX算法中仅包含模加、循环位移、异或3种运算,而循环位移和异或运算以概率1传播,即经过它们运算后的输出差分值是确定的.因此,在计算GFARX算法的差分概率时,只需计算模加运算的差分概率即可.首先给出加法差分方程比特方程

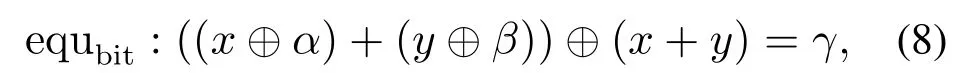
式(8)中:α,β,γ均为常量.根据文献[17]给出模2n加的差分概率计算公式

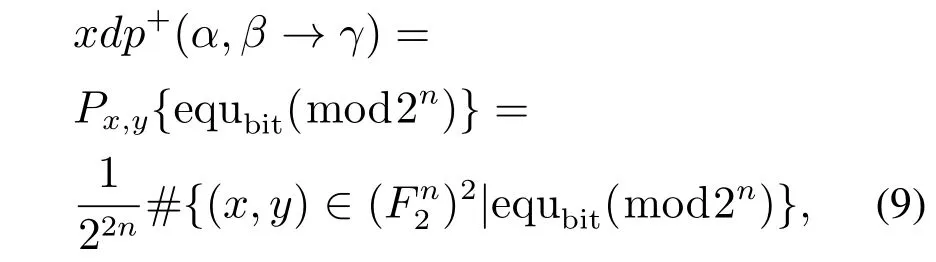
式(9)中:α,β是输入差分,γ是输出差分,代表二元有限域F2的n维向量.为了评估GFARX算法的抗差分性能,本文采用基于SAT/SMT自动化搜索技术[18]进行搜索.由此得到GFARX–128/128算法不存在超过24 轮的有效差分特征.因此算法轮数大于24轮即可认为算法是安全的.

4.4.3 线性分析

线性分析的基本思想是采用算法中的明文、密文以及密钥的不平衡进行线性逼近,将密码与随机置换区分开,在此基础上恢复某些密钥的比特.因此分析者需要寻找一条或多条高偏差的进行线性逼近.为了评估GFARX的抗线性分析能力,本文采用SAT/SMT自动化搜索技术对GFARX–128/128算法进行搜索.得出9轮和10轮最优线性相关度分别为2−21和2−24,因此28轮(9轮+9轮+10轮)的线性相关度不超过2−21×2−21×2−24=2−66<2−64,所以均为线性无效路径.则超过28轮的GFARX算法可以抵抗线性分析.

5 GFARX算法性能实验

本节主要是对GFARX算法进行性能测试;给出了GFARX算法和PRESENT算法在Windows 64位环境和ARM 32位环境下的软件实验结果.具体测试环境为:

· Intel(R)Core(TM) i5-6300HQ CPU@2.30 GHz主频、8 G内存、基于x64的处理器;

·基于STM32L4 微处理器的开发板(主频80 MHz)、64 Kbyte片内RAM、256 Kbyte片内ROM.

在进行性能测试实验时,每次采用同样的256 bytes明文数据作为算法的输入.本文取105次CBC模式下的明文数据加解密测试实验结果的平均值作为实验结果,实验结果用加/解密速率(单位:Mbps)来表示,加/解密速率可用如下公式表示:

加密速率=加密数据大小/加密执行时间,

解密速率=解密数据大小/解密执行时间.

本文给出了在同等环境下的GFARX算法版本以及PRESENT(128/128)算法的实验结果,结果还包含进行密钥扩展的时间.整个实验的测试结果如表5所示.

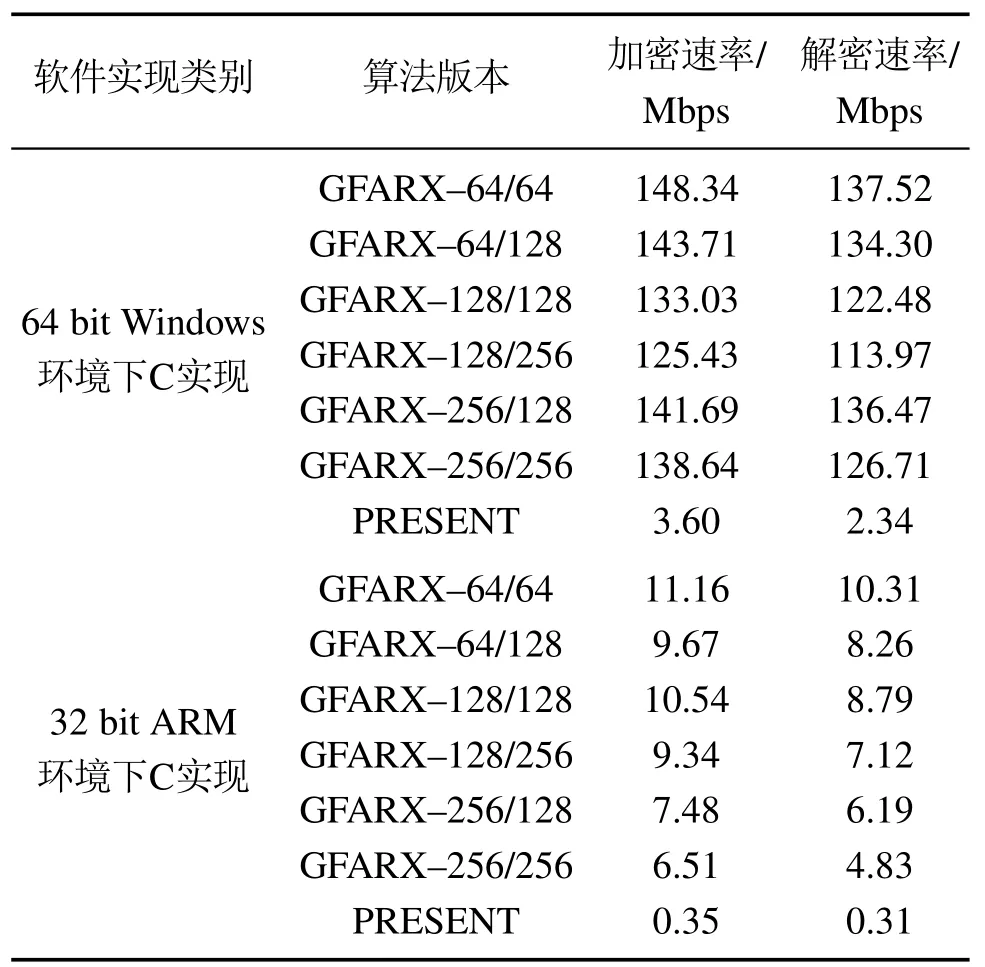
表5 GFARX算法和PRESENT算法加/解密速率Table 5 The encryption/decryption rate of GFARX algorithm and PRESENT algorithm

实验结果表明:

1) 在同等的实验环境下,GFARX–128/128算法是PRESENT(128/128)软件实现效率的30多倍,即本文所采用的ARX结构替换常用分组密码算法的S盒与P盒达到了轻量化的目的;

2) 在相同的密钥长度下,明文分组的长度对性能有一定的影响,具体表现为在4分支的GFARX算法下,明文的分组长度(bit)是系统的CPU位数(bit)的整数倍时,性能更高;

3) 明文长度不是CPU位数的整数倍时,密钥长度越长,由于处理的密钥和轮数更多,因此效率有所下降,但安全性得到提升.

综上,就4分支的GFARX算法而言,128 bit的明文分组更适合32位的CPU平台,而256 bit的明文分组能更好地契合64位CPU平台;因此,也可推断出,64 bit的明文分组也适合于4分支的16位CPU平台.在相应位数CPU的平台下,相应分组长度的GFARX算法更能发挥其优势.若要求性能高,则选择更低的密钥长度;若需要更好的安全性,则选择更长的密钥长度.

6 总结

本文提出了一种基于改进的广义Feistel结构高性能轻量级分组密码算法—GFARX.该算法采用广义Feistel结构,利用模加、循环位移和异或操作构成的ARX结构来替代计算量大、实现复杂的分组密码结构中的S盒和P盒,加快了分组密码算法的运算速度.针对不同位数的CPU平台,本文设计了6种版本的GFARX算法以提升算法的性能.相较于目前的广义Feistel结构密码算法,GFARX算法结构简单,线性部件和非线性部件简单易实现,结构清晰,混淆性和扩散性好,软件实现速率快,提升了轻量级分组密码的执行效率和安全性.

本文虽在结构上对基于广义Feistel结构的分组密码算法进行了改进,但目前算法仅采用了4分支的广义GFARX结构进行了测试实验;由于时间有限,更多分支的情况是否能提升算法的执行效率,有待去发掘.此外,本文仅对GFARX算法进行了软件测试实验,而未进行硬件分析和实现,后续可进一步对算法进行硬件方面的研究.