具有DoS攻击非线性网络的动态事件触发控制

黄 玲,孙晓宇,蔺小娜,郭 婧

(哈尔滨理工大学自动化学院,黑龙江哈尔滨 150080;黑龙江省复杂智能系统与集成重点实验室,黑龙江哈尔滨 150080)

1 引言

随着网络控制系统的普及,网络受到的威胁越来越多,由于网络带宽的限制,网络越来越拥堵,如何在复杂的状况下保持网络控制系统的性能是近期的热点问题.

针对网络带宽限制,基于事件触发的控制方案得到了越来越多的关注[1–3].这种基于事件的策略可以根据需要执行控制操作,降低网络带宽的占用率,从而减少通信消耗[4–7].然而现有的事件触发条件设定的阈值是固定的,这依然会释放对系统性能提升没有意义的多余数据包,因此研究动态事件触发控制方式,根据系统的不同运行状况采用不同的触发参数是非常有意义的,此外,这种动态事件触发能够达到与静态事件触发相同的控制性能,同时减少传输次数.目前基于动态事件触发的控制系统分为两大类,一类是控制与传输的联合设计[8–9];一类是两者分开设计[10–13].文献[8]研究具有执行器故障的非线性系统的可靠事件触发输出控制,该动态触发条件和系统的输出有关.文献[9]研究具有L-2增益的线性定常系统的动态事件触发镇定控制.文献[10]根据Lyapunov泛函的单调递减的思想来设计触发条件,将调度器作为决定控制任务是否执行的反馈控制器来确保控制任务的按时完成与系统的稳定.文献[11]给出了动态触发参数的选择不同对其控制性能以及Lyapunov函数下降率的影响,并且验证了系统的稳定性.文献[12]建立了积分型触发机制,降低了Lyapunov函数的导数小于零的约束,使系统拥有保守性更低的渐近稳定性判据.文献[13]针对基于观测器反馈控制器的线性系统,设计了一种基于局部信息新的动态触发机制.利用线性矩阵不等式,给出了闭环系统渐近稳定和避免芝诺行为的充分条件.

动态事件触发的控制策略对采样数据很敏感,并且由于通信网络的日益开放而容易受到网络攻击[14].DoS攻击是最常见的攻击方式,它可能会阻止控制更新在每个期望的时间执行,这会导致时间延迟或数据包丢失[15–16].DoS攻击造成的时延不同于传统的网络不确定性造成的时延.实际上,DoS攻击可能不遵循任何确定性方式或特定规则,如周期行为或概率分布.基于这一观点,时延方法更适合于描述DoS攻击行为.考虑到DoS攻击的能量约束,对时延越不保守,系统可以容忍越长的DoS持续时间.因此,有必要设计一个安全控制器来容忍更大的时延或丢包.对于安全控制问题,一个重要的步骤是建立描述攻击的规则,常见的有以下3种:假设DoS攻击是周期性部署的,文献[17]在假设攻击通过周期性部分已知的干扰机来实施,推导出一个触发时序,在假设已经检测到干扰信号的周期的情况下,确定何时更新控制信号,由此开发了一个事件触发的弹性控制器.文献[18]假设攻击满足周期性,基于这种假设将攻击下的系统建模为切换系统,并针对不同时期系统设计不同的控制律,完成了观测器和控制器的协同设计.文献[19]在周期性攻击和弹性事件触发通信机制下建立状态误差相关的切换系统模型,设计了网络控制系统基于事件的控制器.假设DoS攻击是随机量,文献[20]将攻击导致的丢包建模为马尔科夫过程,在此基础上网络控制系统被建模为马尔科夫跳跃线性系统从而设计控制器.文献[21–22]将攻击分别通过伯努利随机分布过程和马尔可夫模型来描述.但是文献[21–22]中的DoS攻击模型类似于网络系统中数据包丢失的描述,无法准确描述攻击性质.假设DoS攻击是能量有限的,文献[23]只假设攻击是能量有限的,在这种假设下进行建模设计了多区域电力系统的弹性事件触发控制器.文献[24]提出了攻击频率和攻击持续时间的概念,在此基础上导出了弹性控制策略,以保证物理过程的输入–状态稳定性.文献[25]研究了网络物理系统在以频率和持续时间特性为特征的拒绝服务攻击下的弹性控制问题,建立模型来描述异步攻击信号的递归特征,基于该模型,提出了一种动态事件触发的弹性控制方法.

由于目前将动态事件触发机制与DoS攻击结合的研究较少,具有单边Lipschitz条件[26]的系统研究的更少.故本文研究具有DoS攻击非线性网络的动态事件触发控制是有意义的.本文主要贡献如下:1)对于含有单边Lipschitz条件的网络控制系统中的DoS攻击用动态事件触发条件的不确定性来体现攻击的能量有限性;2)在设计过程中利用拆分法和转化法相结合来解决所求不等式矩阵中含有两种非线性项的问题;3)给出了一种针对非线性系统中存在DoS攻击时,节约网络资源的解决方案.

2 问题的提出

2.1 网络化系统

考虑如下的单边Lipschitz非线性系统:

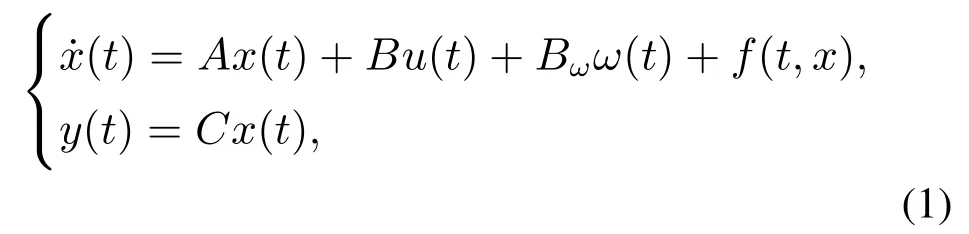
其中:x(t)∈Rn为系统状态变量,y(t)∈Rp为系统输出,u(t)∈Rm为系统输入,ω(t)∈Rn为系统未知扰动,A,B,Bw,C均为已知适当维数常数矩阵,f(t,x)为满足下列假设1和假设2的非线性函数.

假设1f(t,x)满足单边Lipschitz条件

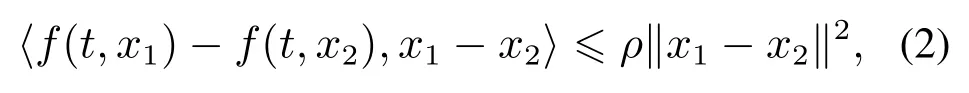
其中ρ ∈R是单边常数.

假设2f(t,x)满足二次内有界条件

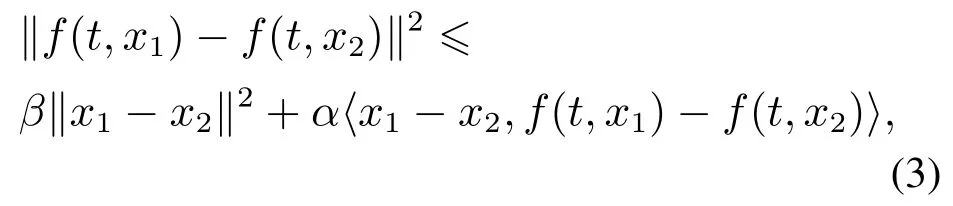
其中β,α ∈R是已知常数.

在上述假设中,〈·〉表示空间中的内积,如:x,y ∈Rn,则〈x,y〉=(xTy).

2.2 DoS攻击建模

在图1中,对状态x(t)按照采样周期h进行采样,传感器采样时刻记为sn=nh,n ∈N,采样数据记为,在每个采样时刻,事件触发器决定最近采样的状态数据是否传输,传输时刻记为tkh,传输数据记为,从而传输时刻序列是采样序列的子集.

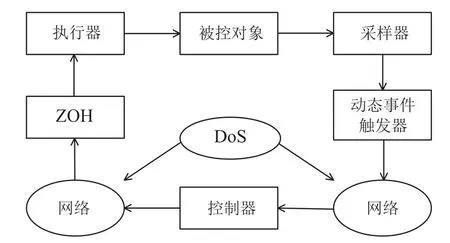
图1 动态事件触发网络控制系统Fig.1 Networked control system with dynamic event trigger

DoS攻击会导致系统的控制性能下降,但并不是所有的DoS攻击都会导致系统崩溃.当发生DoS攻击时,网络控制系统可能会运行在具有一定安全性能的情况中,即由于DoS攻击,最后成功传输的状态值与当前状态值之间的实际误差超出了预期范围.因此,本文将重点讨论引起动态触发条件改变的误差,如图2所示.

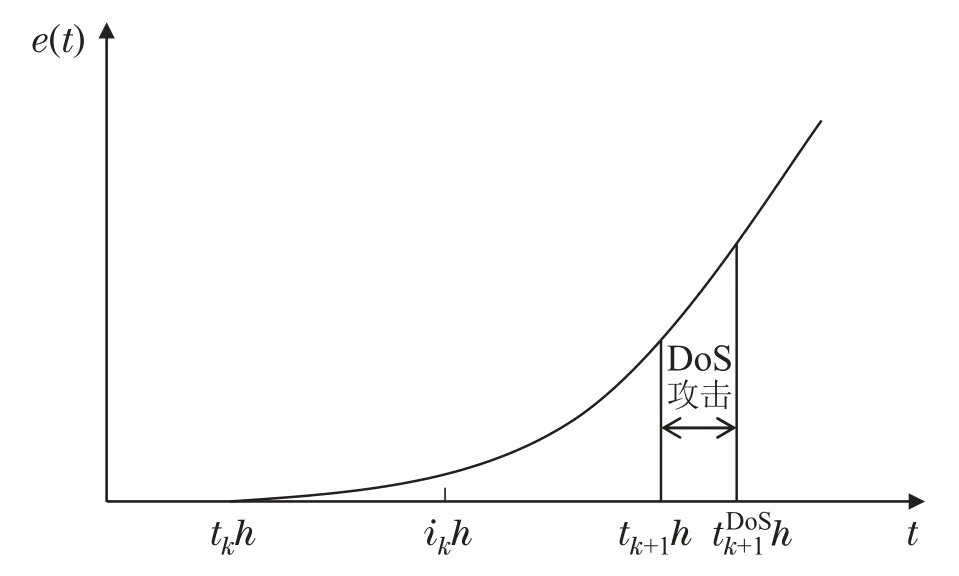
图2 DoS攻击下的控制思想Fig.2 Key idea under DoS attack

首先根据触发条件(无额外触发错误)将上次成功触发的控制更新时间瞬间表示为tkh,将最新触发的采样瞬间表示为tk+1h,但是由于能量有限的DoS攻击,tk+1h可能会延长到.如果将ikh表示为第k个时间间隔内的当前采样瞬间,则给出以下表达式来表示每个采样瞬间的DoS攻击行为

一般来说,在任何时间都可以发起DoS攻击,但攻击的持续时间是有限的,因此可以描述能量有限的DoS攻击为

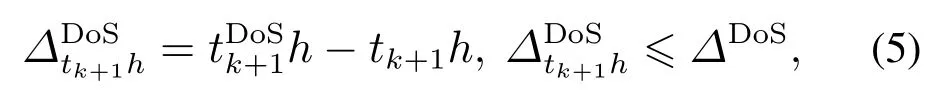
其中∆DoS表示DoS攻击的最长持续时间.

2.3 动态事件触发控制策略

定义

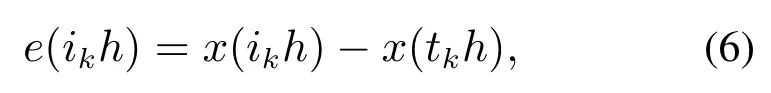
其中:x(ikh)是当前状态值,x(tkh)是上次成功更新的状态值.

同理,DoS攻击引起的额外误差为

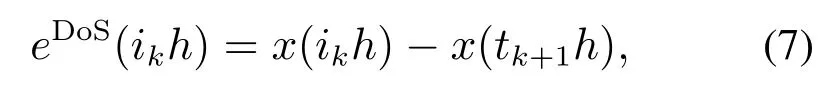
其中x(tk+1h)是最新触发的状态值.

由上述分析,DoS攻击下的动态事件触发策略为

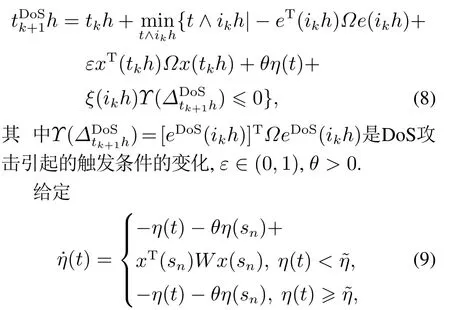
其中:sn=nh,n ∈N是传感器采样时刻,˜η是根据实际情况进行调整的参数,W >0是需设计权值矩阵,该动态变量在初始值η(0)=η0非负情况下始终非负.

两次成功传输间的控制输入为

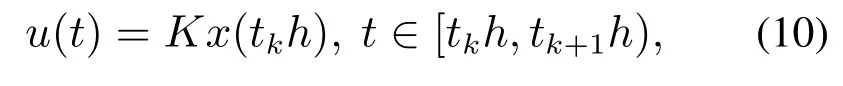
定义

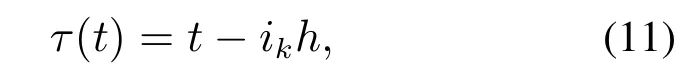
则闭环系统为

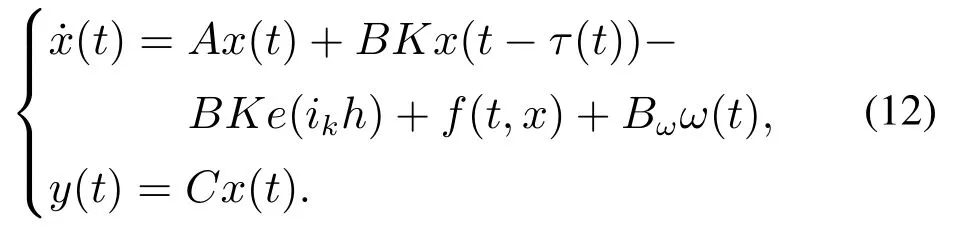
考虑到DoS攻击引起的触发条件的变化,设计控制器保证闭环系统稳定是一个值得关注的问题.具体的控制目标为

1) 当不存在DoS攻击时,闭环系统(12)在ω(t)=0时是渐近稳定的,在存在扰动时具有H∞性能,即∥y(t)∥≤γ∥ω(t)∥.

2) 当存在DoS攻击时,可以获得最终一致有界的安全性能,即性能损失∥Lx(t)∥≤C,其中C为性能损失的上界.

注2动态事件触发策略(8)基于网络化系统的采样周期h触发.触发策略(8)表明两个事件执行时刻的最小时间间隔为h,触发信号的传输只发生在采样时刻,由于采样周期h为大于零的常数,从而避免了芝诺行为.同时,结合引理3可得,当θ >0时,动态事件触发相对于静态事件触发的触发次数少,从而节省了网络资源.

引理4(Young’s不 等 式[27]) 任 意a,b ∈Rn,ϑ>0,任意Π >0,有

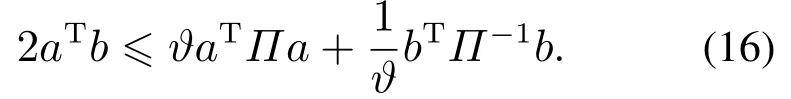
引理5[26]对于具有合适维度的矩阵Ψ,G,T,H和标量ξ,如果满足下列条件:

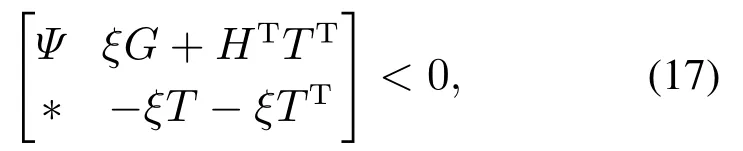
则下列不等式成立:

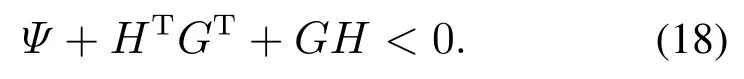
3 主要定理及其证明

在本节中,给出了满足控制目标1)和2)的LMI形式的充分条件.

定理1给定正常数h,ρ,β,α,ε,σ,γ,τm≥0,τM(≥τm),若存在正标量ε1,ε2及对称正定矩阵P,Qi,Zi,S,W,Ω(i=1,2),使得不等式(19)–(20)成立

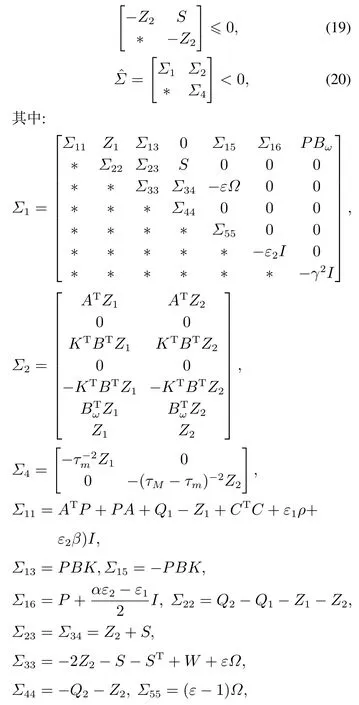
则闭环系统(12)具有以下性能:

1) 当没有DoS攻击时,系统(12)在ω(t)=0的情况下渐近稳定,在有扰动时具有H∞性能.

2) 当存在DoS攻击时,一致最终有界的安全性能

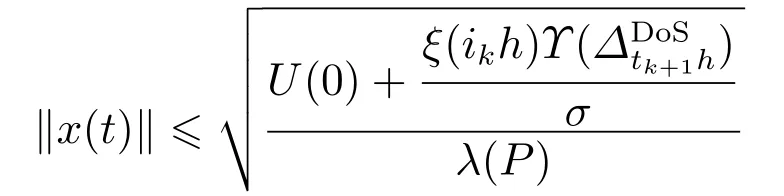
是在性能损失

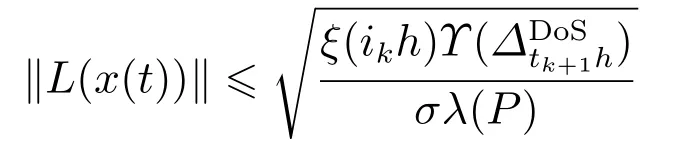
的情况下实现的,其中

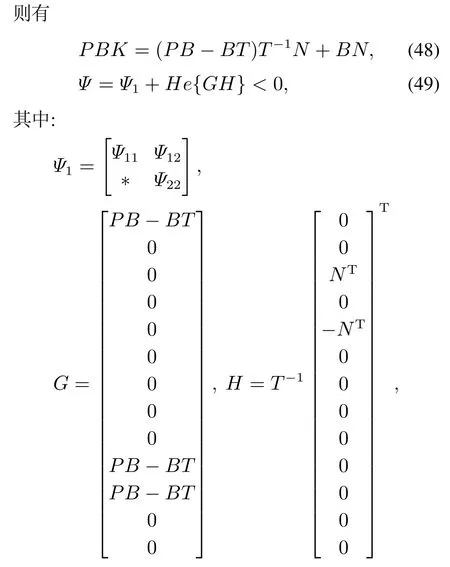
其中Ψ11,Ψ12及Ψ22如定理2中所示.

由引理5,式(49)可写为式(44)形式.则式(44)得证.所以闭环系统(12)在不存在DoS攻击的情况下渐近稳定,且具有H∞的干扰衰减性能指标.基于所设计的控制器,可以实现目标2).

由上所述,定理2成立. 证毕.

注3中有两种非线性项,分别为ZiBK(i=1,2)和PBK,其中Zi,P,K都是未知的,因此无法处理同时含有这两种耦合的不等式,所以本文使用两种方法对非线性项进行处理.首先第1种是拆分法,使用引理4和Schur补引理将ZiBK项中的BK项分离出来,凑成非线性项PBK,这样就转化成一种非线性项.然后利用第2种转化法,引入非奇异矩阵替代非线性项PBK,结合引理5将其转化为线性的.

4 仿真

考虑钟摆例子[29],其系统参数为

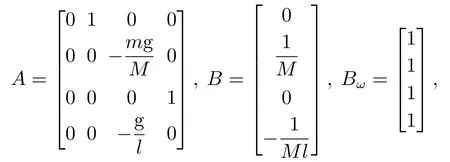
其中:M=10 kg是小车质量,m=1 kg是摆锤质量,l=3 m是摆臂长度,g=10 m/s2是重力加速度.初始状态为x(0)=[0.98 0 0.2 0]T,取采样周期h=0.01 s.当没有控制输入时,很容易看出系统是不稳定的.根据本文的控制器设计方法,选择参数

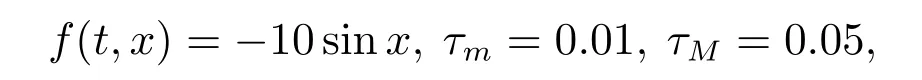
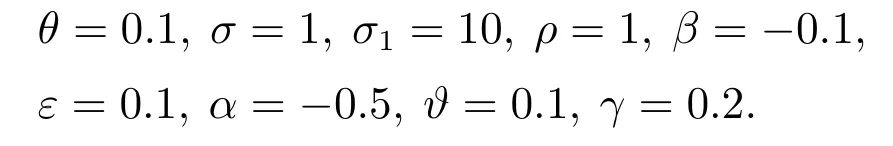
然后得到相应的反馈控制器和触发矩阵

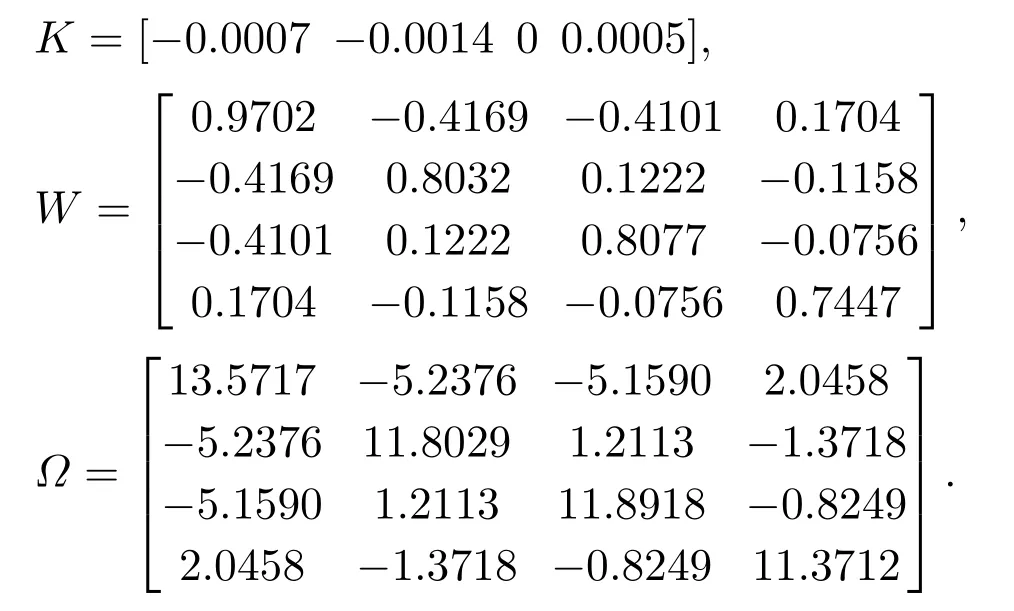
下面的3种情况说明不同Υ值对系统的影响,即DoS攻击下的性能损失.

1)Υ=0:当不存在DoS攻击时,动态事件触发方案下的状态响应如图3所示,触发时间和触发序列如图4所示.在这种情况下,有154个数据被传输.图3表明系统状态以良好的性能收敛到零,也就是说没有性能损失,故此时C=0.

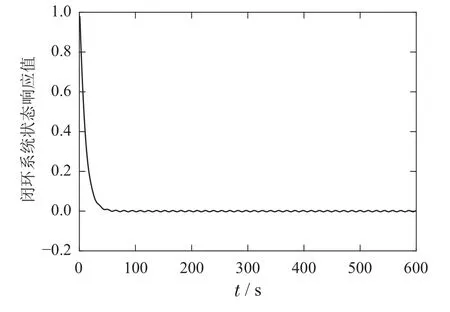
图3 无DoS攻击的状态响应Fig.3 State response without DoS attack

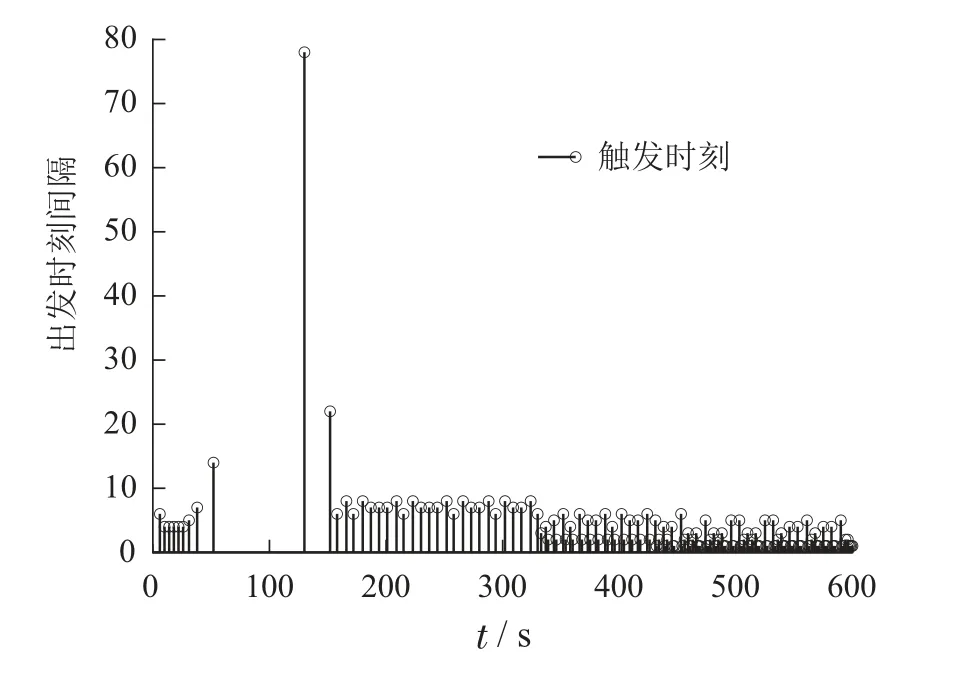
图4 无DoS攻击的触发序列Fig.4 Trigger sequence without DoS attack

2)Υ=0.1:当存在弱DoS攻击时,通过设计的控制器,动态事件触发方案下的状态响应如图5所示,触发时间和触发序列如图6所示.在这种情况下,有121个数据被传输,传输次数减少,此时C=0.1148.对比图5和图3可看出,在这种DoS方式下,性能较差,说明DoS攻击确实会导致性能较差.

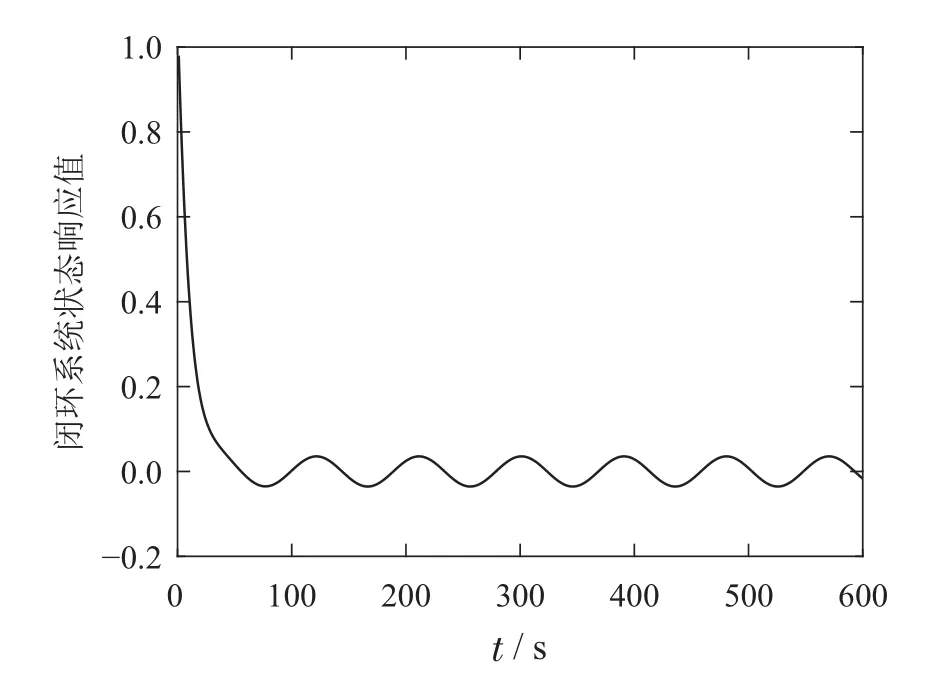
图5 弱DoS攻击的状态响应Fig.5 State response with weak DoS attack

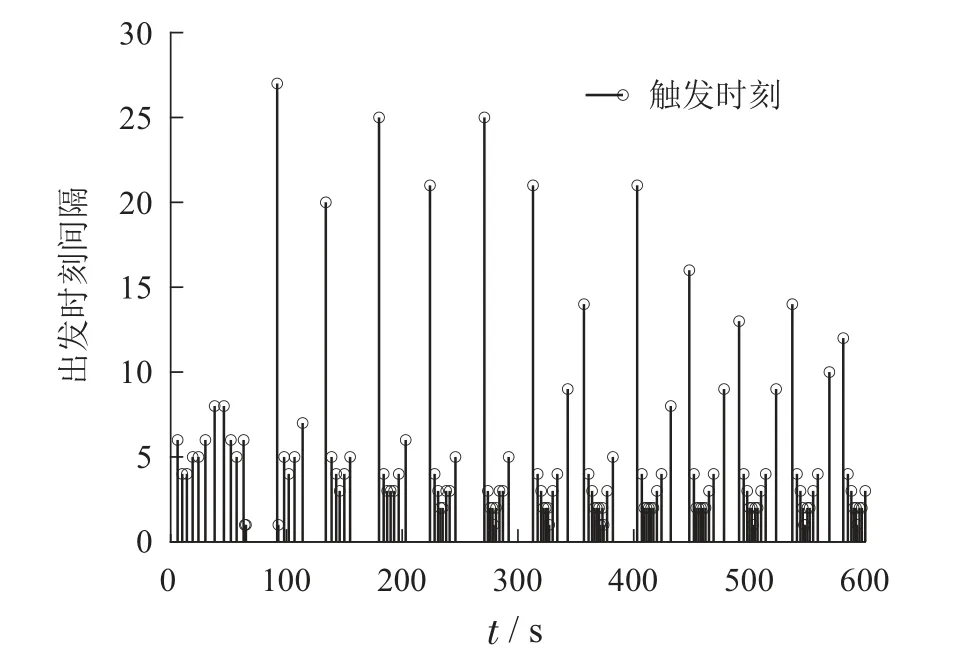
图6 弱DoS攻击的触发序列Fig.6 Trigger sequence with weak DoS attack

3)Υ=0.7:当存在强DoS攻击时,通过设计的控制器,动态事件触发方案下的状态响应如图7所示,触发时间和触发序列如图8所示.在这种情况下,有66个数据被传输,此时C=0.7686.虽然∥x(t)∥是有界的,但比较图7和图3可知,图7有更差的性能.

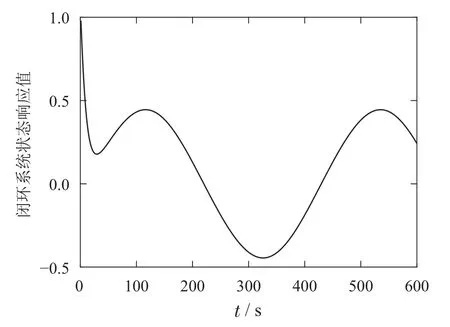
图7 强DoS攻击的状态响应Fig.7 State response with strong DoS attack

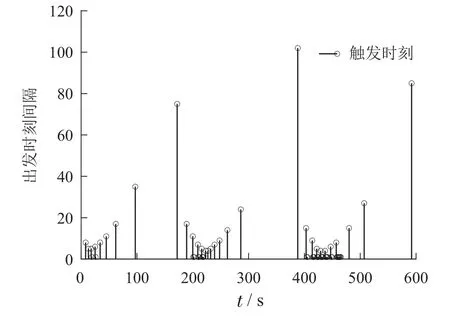
图8 强DoS攻击的触发序列Fig.8 Trigger sequence with strong DoS attack

从上面的仿真可以看到,Υ越大,传输次数越少,控制性能越差.这意味着在实际工程中可以权衡控制性能和网络安全.

5 结论

本文通过动态事件触发策略研究具有DoS攻击网络化系统控制问题,解决了网络化系统在传感器到控制器受到DoS攻击时,系统控制器的设计问题.通过DoS攻击引起的不确定性推导出系统渐近稳定时控制器存在的充分条件,与以往静态触发研究的不同,本文采用基于动态触发条件的控制策略,在保证系统稳定的前提下,减少了触发次数,节约网络资源.最后用一个数值例子验证了研究结果的有效性.