带有运行成本函数的Hamilton-Jacobi可达性分析
廖 玮,梁涛涛,魏小辉
(南京航空航天大学机械结构力学及控制国家重点实验室,江苏南京,210016;南京航空航天大学飞行器先进设计技术国防重点学科实验室,江苏南京,210016)
1 引言
可达性分析是一种描述非线性控制系统行为的重要方法[1],在可达性分析中,首先需要在状态空间中指定一个集合作为目标集,再给定一个时间范围,目的是在状态空间中计算出一个集合,使得以这个集合内的状态作为初始状态的系统的演化轨迹能够在给定的时间范围内到达目标集,这样的集合也被称为可达集[2].
计算可达集是一件十分具有挑战性的工作,除了一些特殊情况[3],精确地描述可达集几乎是不可能的.在实际的工程问题中,通常的做法是计算可达集的近似表示.在过去的几十年里,人们提出了许多计算可达集的数值方法,这些方法可以分为两类:拉格朗日法[4]和水平集方法[2,5].其中拉格朗日法主要包括椭球法[6–9]和多面体法[10–12],这一类方法可以解决具有高维状态空间的问题,但是对于动力学系统的形式有着较高的要求,主要用于计算线性系统的可达集.而水平集方法对动力学系统的形式没有过多的要求,可以计算非线性系统的可达集,一些学者还开发了基于水平集方法的成熟的可达集计算工具箱[13–14],由于这些原因,水平集方法在工程中得到了广泛的应用,常被用于飞行控制系统[15–16,18]、地面交通系统[17,19]和空中交通系统[14,20]等领域.
水平集方法的基本原理是构造一个无运行成本函数的Hamilton-Jacobi(HJ)方程,该方程的末端条件是一个关于目标集的符号距离函数.用数值方法求解这个HJ方程,并将可达集表示为该方程的解的零水平集.使用水平集方法前,需要在状态空间中指定一个区域作为计算域,并将该区域划分为笛卡尔网格结构.在计算过程中,HJ方程的解在网格点处的值被存放在一个n维数组中,其中n表示状态空间的维数,最终的解通过这个n维数组的插值获得.
水平集方法的原理也决定了该方法对于存储空间的苛刻要求,若要保存某一给定时间范围内的可达集,则需要保存HJ方程在某一时刻的解,其消耗的存储空间会随着系统状态空间的维数指数增长[21],若要保存在若干个不同时间范围内的可达集,则需要保存HJ方程在若干个不同时刻的解,这又会导致存储空间的消耗数倍地增加.这一局限性在一定程度上制约了水平集方法的发展和应用.
为了克服这一局限性,本文提出了一种新的可达集的表示方法.与水平集方法的不同之处在于,该方法将不同时间范围内的可达集表示为一个状态空间中的值函数的不同的非零水平集,这个值函数是一个带有运行成本函数的HJ方程的解.通过保存这个HJ方程在某一个时刻的解即可保存不同时间范围内的可达集,这些可达集用该解不同的非零水平集刻画,从而极大地节约存储空间.综上所述,本文的主要贡献如下:1)本文指出可达集可以表示为一个HJ方程的解的非零水平集,这种表示方法可以极大地节约存储空间;2)为了求解上述HJ方程,本文采用了一种基于递归和插值的数值方法;3)为了验证方法计算结果的准确性和在节约存储空间方面的优越性,本文展示了一些算例.
2 可达集的相关概念
2.1 可达集的定义
考虑如下控制系统:

其中:s ∈Rn是系统的状态,u ∈U是控制输入.函数f(·,·):Rn×U →Rn有界.令U表示从时间区间[0,∞)到集合U上的所有的Lebesgue可测函数构成的集合.若给定了t0时刻的状态以及控制输入u(·)∈U,则系统(1)在时间区间[t0,t1]上的演化过程可以表示为一条轨迹,且.在给定了目标集K和时间范围T后,可达集的定义如下[1–2,18]:
定义1(可达集)
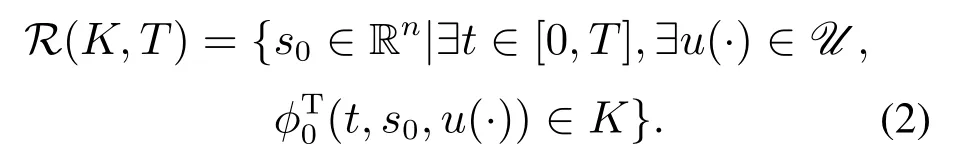
从可达集的定义可知,总是存在一个控制输入u(·)∈U,可以使得从可达集出发的系统的演化轨迹在时间T内到达目标集K.
2.2 水平集方法
水平集方法将可达集和如下最优控制问题联系起来:
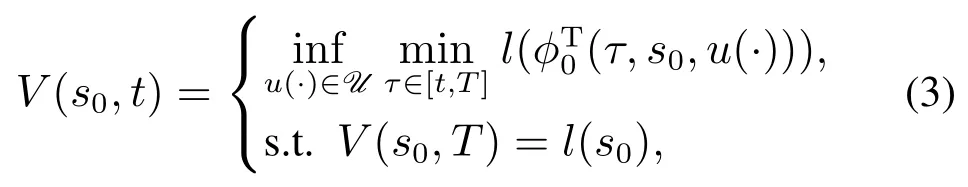
其中V(·,·):是一个状态空间中的时变标量函数,末端条件l(·)是一个有界且Lipschitz连续的标量函数,并满足K={s0∈Rn|l(s0)≤0}.在水平集方法中,可达集被表示为函数V(·,0)的零水平集,即
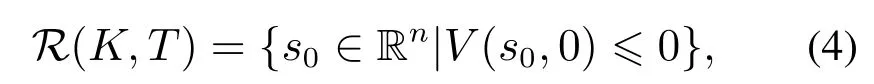
而函数V(·,·)在t时刻的解V(·,t)可以通过数值求解如下HJ方程获得
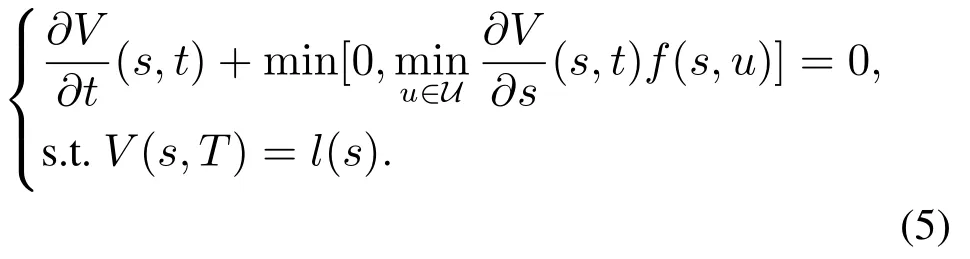
在使用基于水平集方法的工具箱时,用户首先需要在状态空间中指定一个区域作为计算域,并将该区域划分为笛卡尔网格结构,V(·,t)在各网格点处的值都被保存在一个n维数组中,若计算域在第i个维度上被划分为了Ni个网格点,则保存可达集R(K,T)所需要消耗的存储空间正比于.
需要指出的是,若要将时间范围为T1,···,TM的可达集,即R(K,T1),···,R(K,TM),都保存下来,则需要保存函数V(·,·)在T −T1,···,T −TM时刻的值,也就是V(·,T −T1),···,V(·,T −TM).此时消耗的存储空间正比于.
3 基于带有运行成本函数的HJ方程的可达集表示方法
本节将详细介绍基于带有运行成本函数的HJ方程的可达集表示方法,并从一种以Lagrangian项为性能指标的最优控制问题的角度推导出该结论.
3.1 HJ方程的构造
将原系统做如下改动,获得一个新的系统:
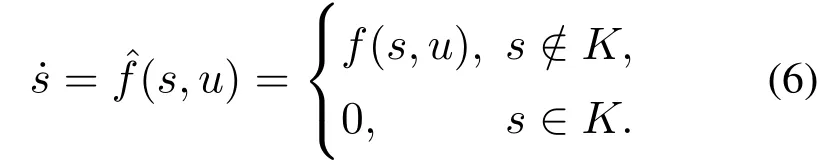
并构造一个运行成本函数c(·):Rn →R:
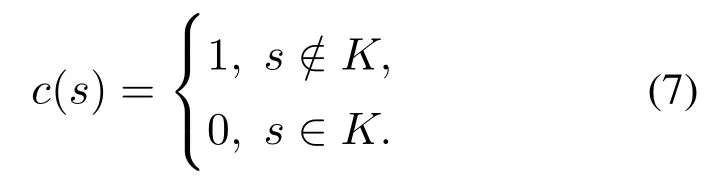
构造如下关于W(·,·)的HJ方程:
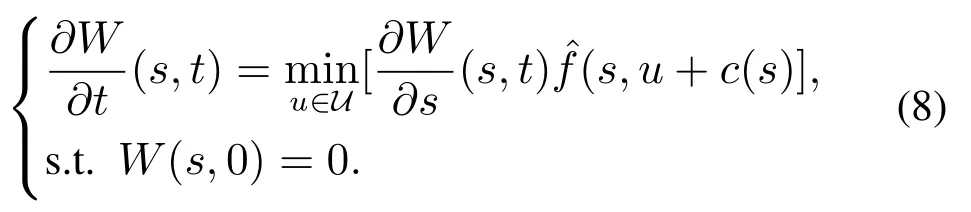
3.2 可达集的表示方法

接下来将证明上述结论.考虑如下情况:控制输入u(·)∈U的目的是为了以尽可能短的时间将系统的状态从初始状态转移至目标集内,在这种情况下,若系统的一条演化轨迹能够在T的时间内到达目标集,那么这条轨迹的初始状态应当属于可达集R(K,T).构造如下标量函数:

其中tf是末端时刻,且tf自由.直观地说,当以s0为初始状态的系统的演化轨迹在容许的控制下能够到达目标集时,表示系统的演化轨迹从s0到达目标集所需的最短时间,否则的值为无穷大.于是
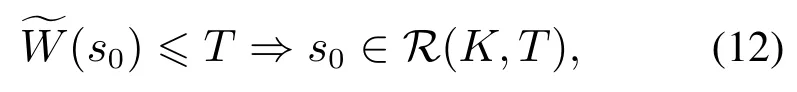
因此,可达集R(K,T)可以表示为
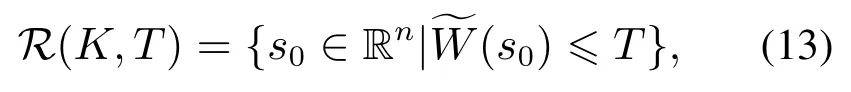
式(11)中包括一个最优控制问题,这个最优控制问题以一个Lagrangian项为性能指标,并且带有末端状态约束.
构造另一个标量函数:
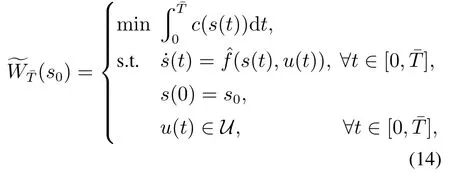
可以得到如下定理:


3.3 最优控制律
在水平集方法中,t时刻,状态s处的最优控制输入为[2,23]
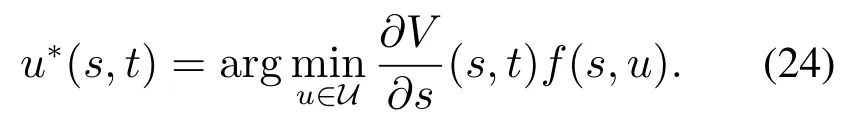
若初始状态s0位于可达集R(K,T)内,则在式(24)的控制律的作用下,系统从s0出发的状态的演化轨迹能够在T的时间内到达目标集.由于V(s,t)的值会随着时间t变化,这意味着,实现式(24)的控制律需要将时间区间[0,T]内各个时刻t的V(s,t)都保存下来,这显然会消耗大量的存储空间.
定理3设计如下最优控制律:
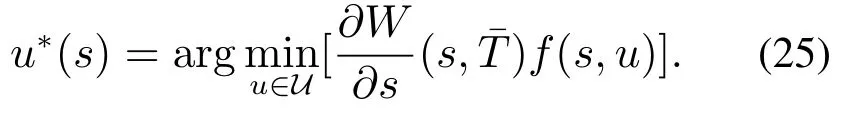
若s0∈R(K,T)且T <,则在式(25)的控制律的作用下,系统从s0出发的状态的演化轨迹能够在T的时间内到达目标集.
证把在u的作用下,经过dt的时间,从状态s转移到的状态为s+f(s,u)dt.最佳的u应当使得(s+f(s,u)dt)最小,即

定理3表明,用本文方法设计控制律时只需要保存式(8)的方程在时刻的解,相对于水平集方法可以极大地节约存储空间.
4 HJ方程的求解
第3.1节中构造了HJ方程,第3.2节指出该方程的解的非零水平集可以表示可达集.然而,求解该方程并非易事,由于系统(6)和运行成本函数(7)不连续,这会导致HJ方程的解对状态的偏导数在某些状态无法定义,甚至有时该方程的解自身在状态空间中都不连续.为此本文将采用一种基于递归和插值的方法求解该方程.
4.1 解的递归格式
当时间步长∆t足够小时,对于任意k ∈N,控制输入u(·)在时间区间[k∆t,(k+1)∆t]上的值可以视为常数,并且系统(1)可以离散化为
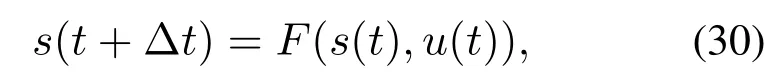
这一离散形式可以通过简单的向前差分法获得,为了更高的精度,也可以使用Runge-Kutta法.于是,系统(6)的离散形式为
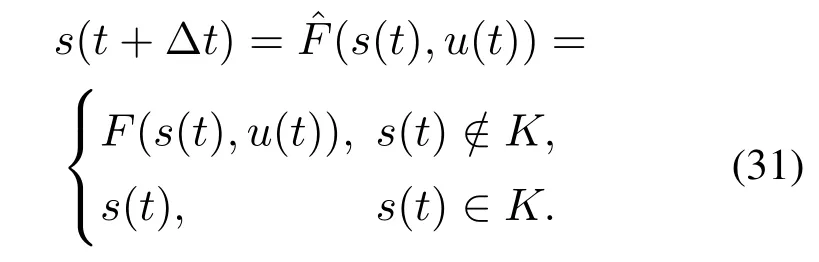
然后可以获得Hamilton-Jacobi-Bellman方程解的递归格式:
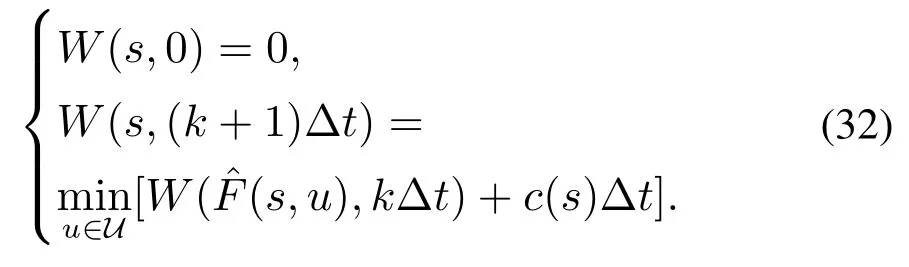
4.2 解的近似
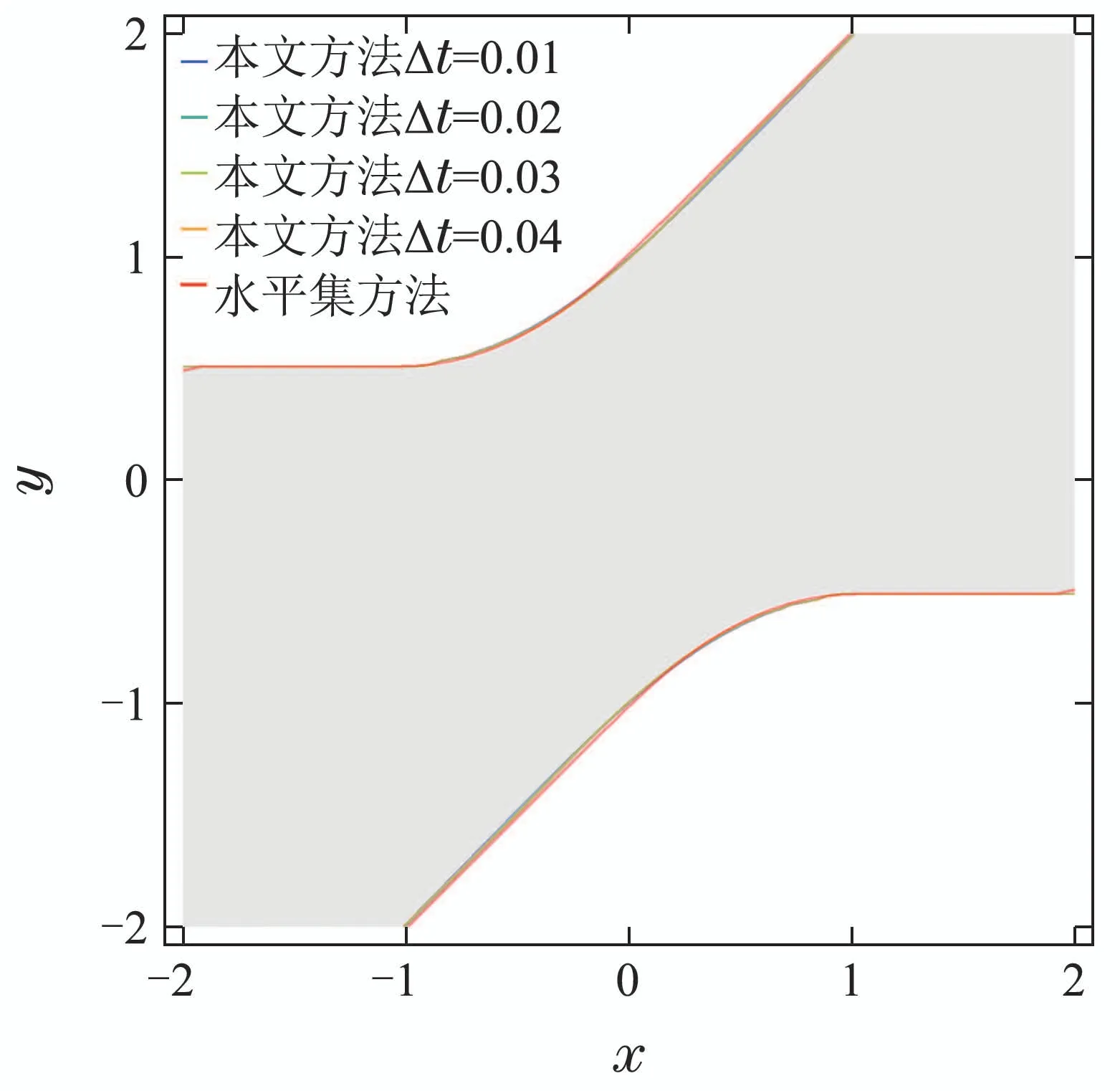
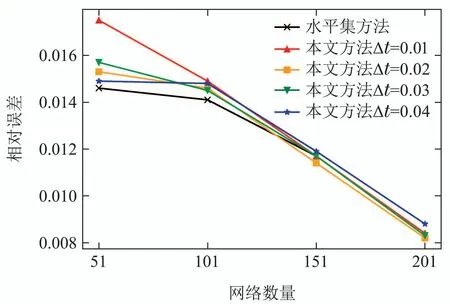
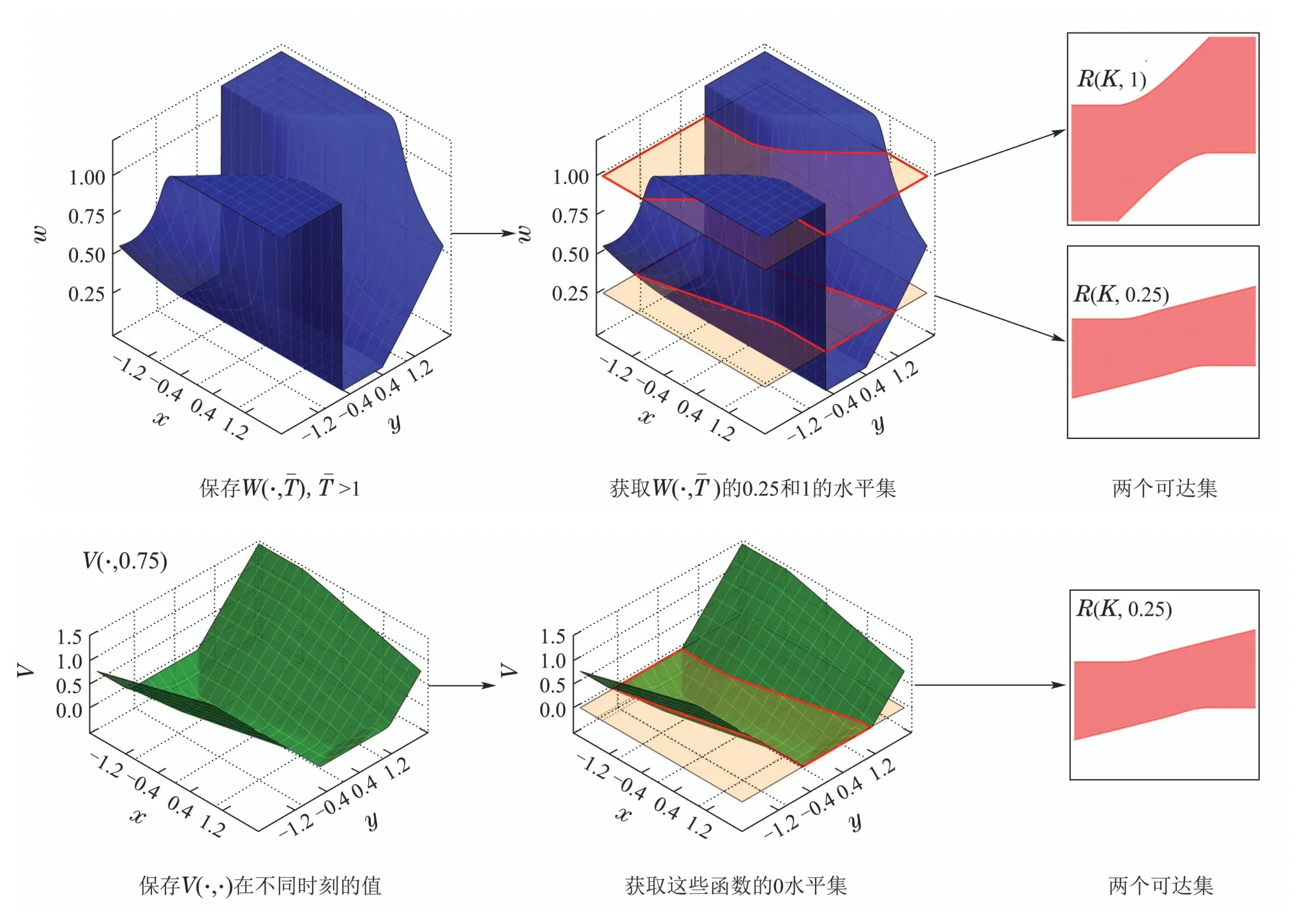
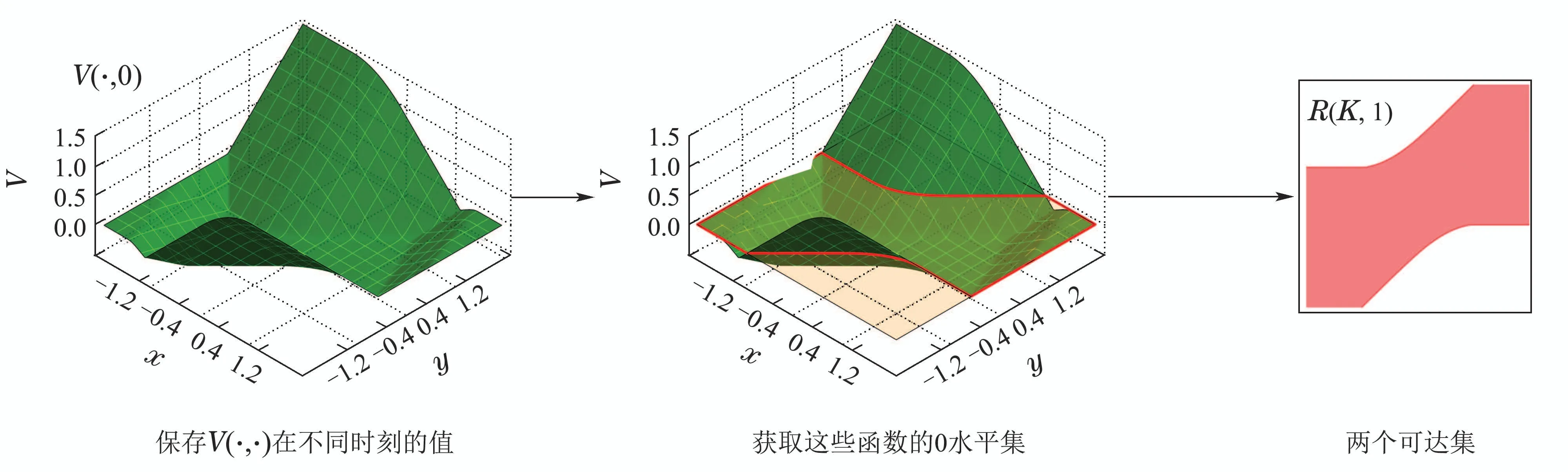
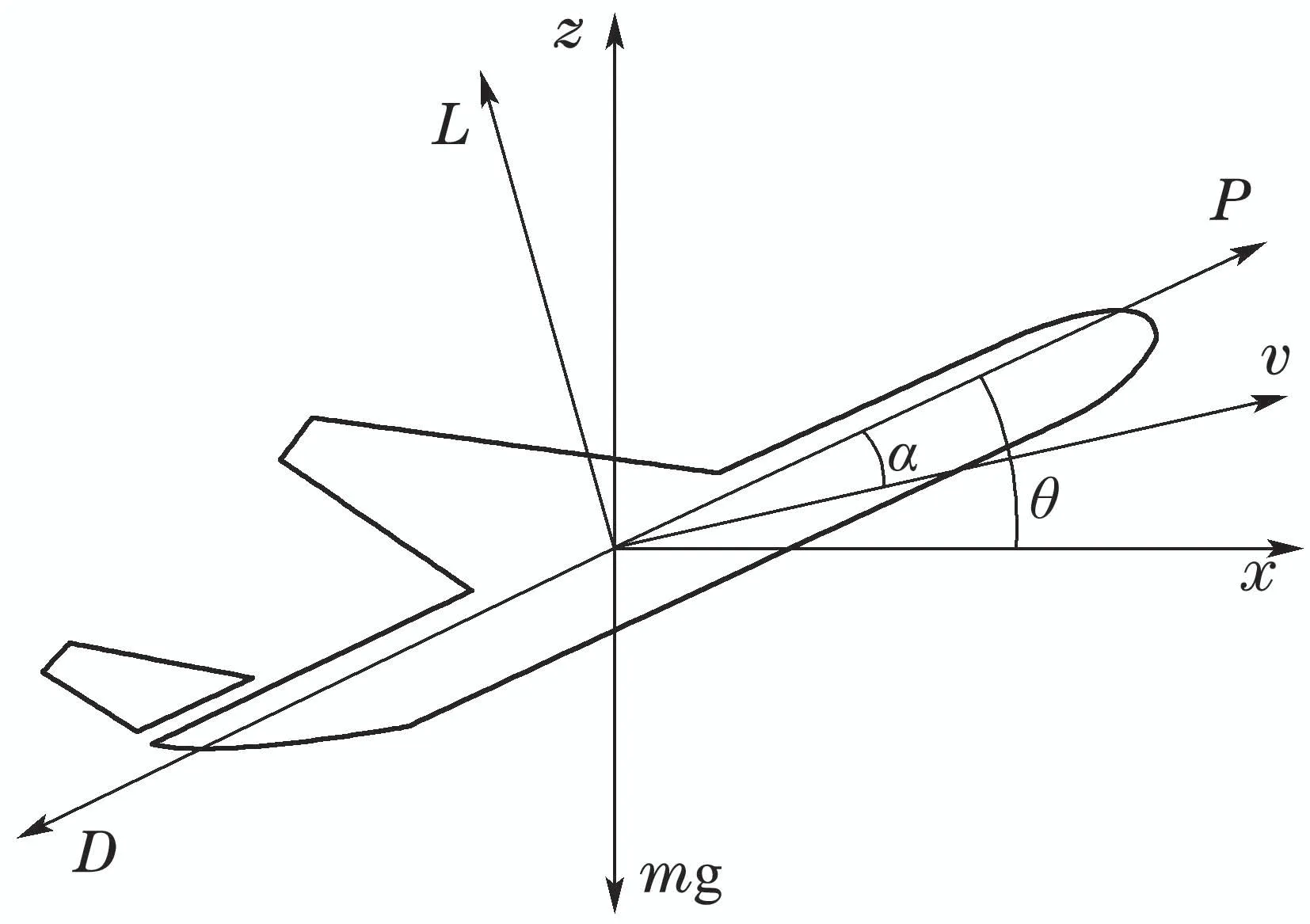
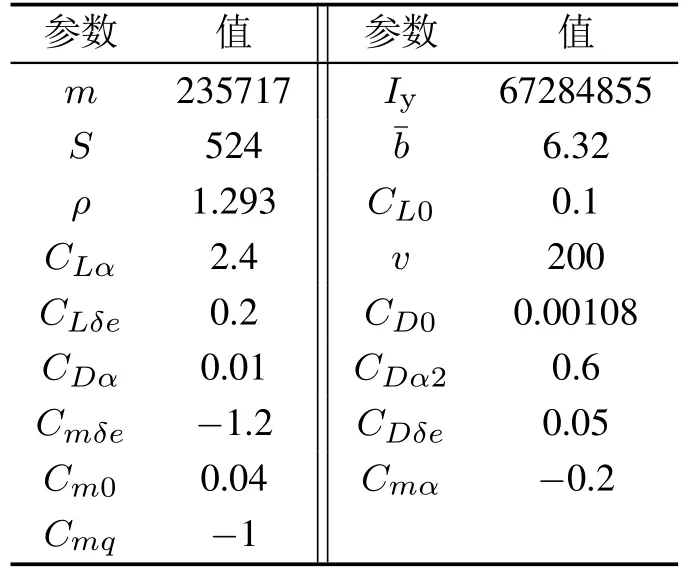
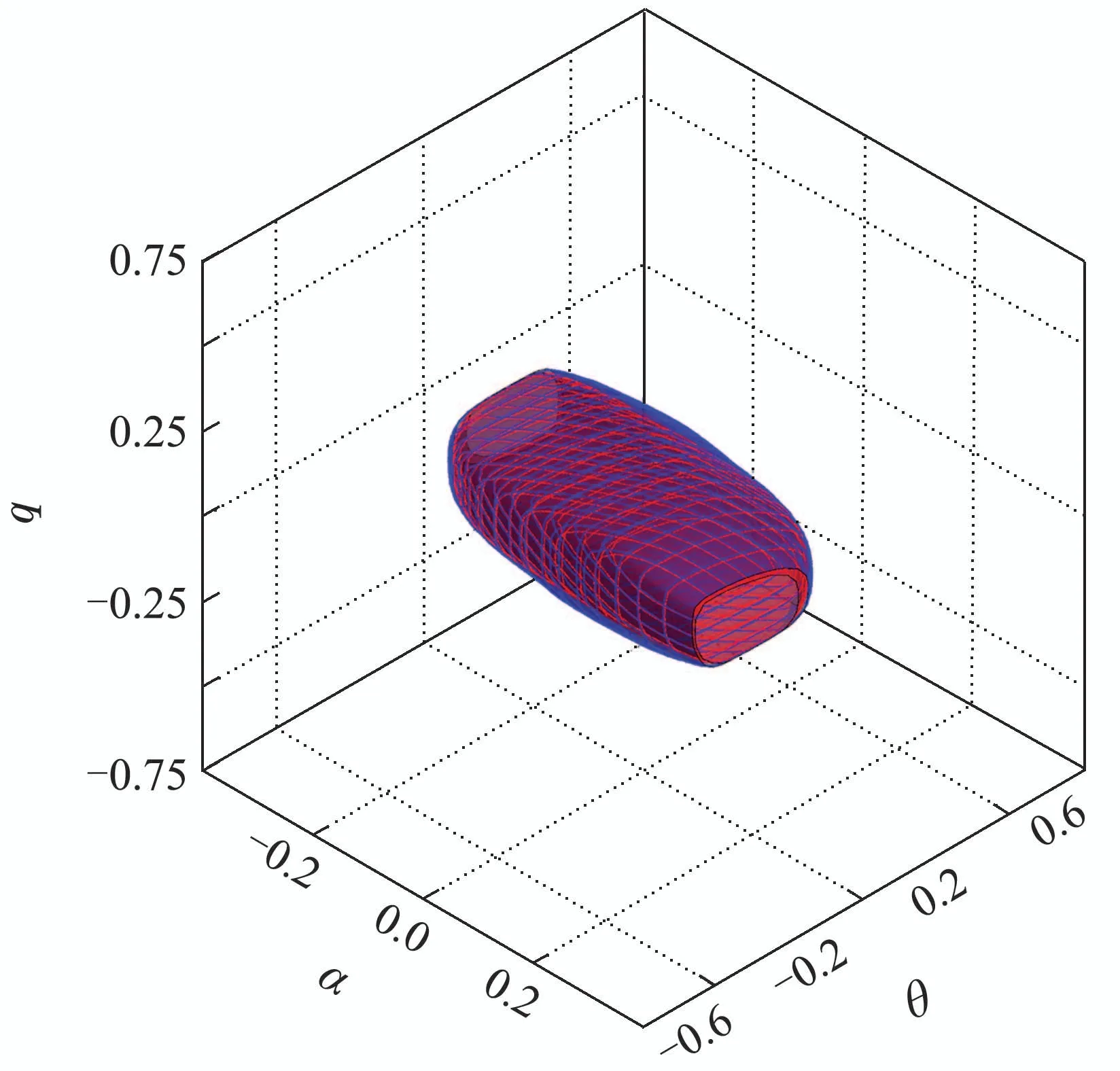
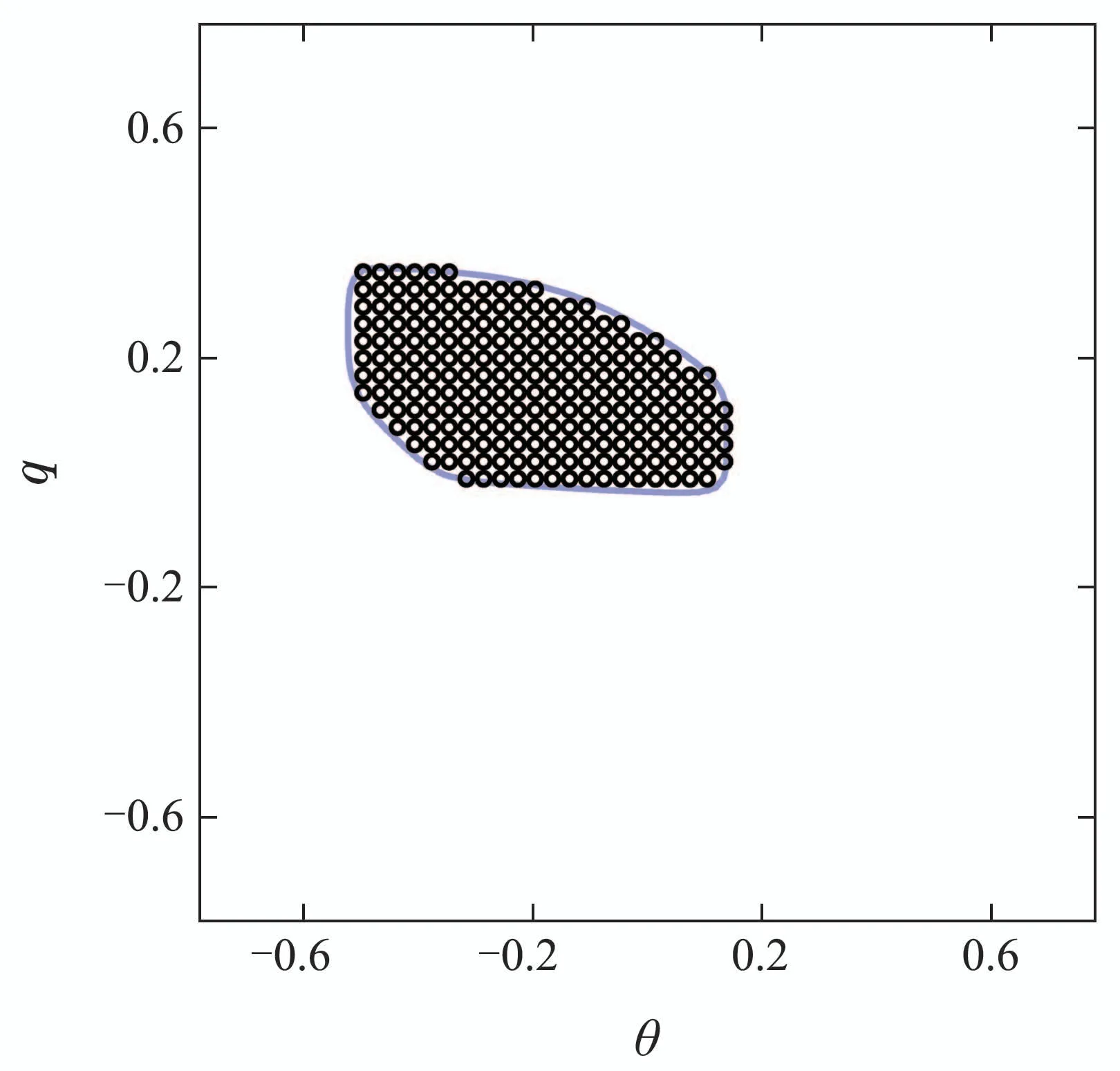
一般情况下,对于任意k ∈N,W(s,k∆t)的解析形式都是难以获得的,本节将采用一种基于插值的方法逼近W(s,k∆t).首先在状态空间中指定一个计算域,并将该计算域划分为笛卡尔网格结构,把函数W(·,k∆t)在网格点处的值保存至一个数组中,数组的维数与状态空间的维数相同.以一个三维系统为例,假设该系统的状态s=[x y z]T,在这种情况下,函数W(·,k∆t)可以用上述三维数组的三重线性插值[24]近似.求解过程的伪代码如表1所示.表1算法输出的结果即是W(s,h∆t)的近似.由算法1可知,对于一个n维的系统,保存W(·,h∆t)所消耗的存储空间正比于,若0 表1 HJ方程的求解方法Table 1 Method for solving the HJ equation 本节以一个简单的二维系统为例,分析了在不同网格数量和时间步长下的计算结果,并将计算结果和水平集方法和解析解对比.考虑如下系统: 其中s=[x y]T∈R2是系统的状态,u ∈U=[−1,1]是控制输入.目标集K={[x y]T||y|≤0.5},时间范围T=1.可达集R(K,T)的解析解是 使用本文提出的方法计算可达集时,计算域设置为[−2,2]×[−2,2],网格数量设置为201×201,时间步长∆t设置为0.01,0.02,0.03,0.04.为了确保递归次数h满足h∆t>T,递归次数h设置为其中Int表示向下取整.此外,本文还将计算结果与水平集方法进行了对比,使用水平集方法计算时,计算域和网格数量的设置与本文提出的方法相同.计算结果如图1所示.可以看出,本文提出的方法的计算结果和解析解十分接近,其精度与水平集方法无显著差异,而且计算结果对时间步长不敏感. 图1 不同方法的计算结果(图中灰色区域表示解析解)Fig.1 Computation results of different methods (the analytical solution is expressed in gray) 为了分析计算精度和网格数量的关系,还尝试了51×51,101×101,151×151等网格数量.为了量化计算结果的精度,采用Jaccard指数[25]度量各计算结果和解析解之间的相对误差,将该误差定义为 图2展示了各方法的相对误差随网格数量的变化,可见在相同的网格数量下,本文方法的精度和水平集方法相当. 图2 相对误差随网格数的变化Fig.2 Variation of relative error with the number of grids 前文中提到,本文方法的优势在于可以极大地节约存储空间.以R(K,0.25)和R(K,1)这两个可达集为例,图3直观地展示了本文方法相对水平集方法在存储空间消耗方面的优势.本文方法只需保存W(·,¯T)即可,其中¯T >1,而水平集方法则需要保存V(·,0.75)和V(·,0),其存储空间消耗是本文方法的两倍. 图3 本文方法和水平集方法保存可达集的方式Fig.3 The ways the proposed method and the level set method save the reachable sets 飞机的纵向模态指的是飞机在自身对称面(xz平面)内的子系统,包括4个状态量,分别是速度v、迎角α、俯仰角θ和俯仰角速度q,如图4所示. 图4 飞机纵向动力学模型Fig.4 Longitudinal dynamic system of an aircraft 其微分方程为[21] 其中s=[v α q θ]T表示飞机的状态,P是推力,m是飞机的质量,ρ是空气密度,Iy是绕y轴的转动惯量,CL,CD和Cm分别是升力系数、阻力系数和俯仰力矩系数,它们的表达式如下: 其中δe ∈[−0.3 0.3]是升降舵转角,并被视为控制输入u,表示平均空气动力弦.在本例中,假设推力P会变化,以保持速度大小v为一个常量.即 在该假设下,系统的状态空间转化为了一个三维的空间,即s=[α q θ]T. 本例中的目标集K=[−0.05,0.05]×[−0.1,0.1]×[−0.1,0.1],时间范围T=1,样例飞机的各参数如表2所示. 表2 样例飞机的物理参数Table 2 Physical parameters of the reference aircraft 使用本文方法计算可达集时,各参数设置如下: 1) 计算域:Ω=[−0.4,0.4]×[−0.75,0.75]×[−0.75,0.75]. 2) 网格数量:101×101×101. 3) 时间步长:∆t=0.01. 4) 递归次数:101. 计算结果如图5所示.图蓝色包络面是本文方法的计算结果,红色包络面是水平集方法的计算结果,使用这两种方法时,计算域和网格数量是相同的.可见本文方法的计算结果和水平集方法是十分接近的. 图5 纵向飞行控制系统可达集Fig.5 Reachable set of the longitudinal flight control system 为了验证式(25)的控制律的有效性,检验了状态空间中的一些初始状态能否在该控制律的作用下在T的时间内转移至目标集.图6展示了状态空间的一个切片,图中的圆形空心点表示能够在T的时间内转移至目标集的初始状态,蓝色的曲线是可达集的轮廓.可见,圆形空心点几乎完全分布在可达集的轮廓内,这表明式(25)的控制律是有效的. 图6 最优控制律的验证Fig.6 Verification of optimal control law 本文构造了一个带有运行成本函数的HJ方程,使用该方程的解的非零水平集表示可达集.为了求解该方程,本文采用了一种基于递归和插值的方法.此外,还基于该方程的解为可达集设计了最优控制律.本文的最后用一些算例验证了所提出的方法的有效性.主要结论如下: 1) 不同时间范围的可达集都可以用所构造的HJ方程在某一个时刻的解的不同的非零水平集表示,这种表示方式相对于传统的水平集方法可以极大地节约存储空间. 2) 使用所构造的HJ方程在某一个时刻的解即可为可达集设计最优控制律. 3) 使用递归和插值可以有效地求解本文构造的HJ方程,使得计算出的可达集有着与水平集方法相当的精度.
5 数值算例
5.1 二维系统算例
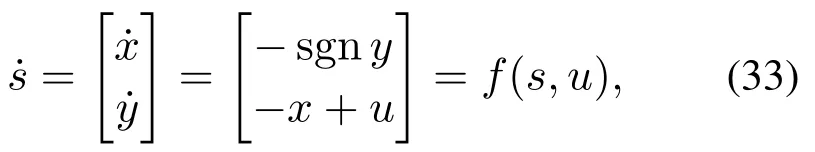
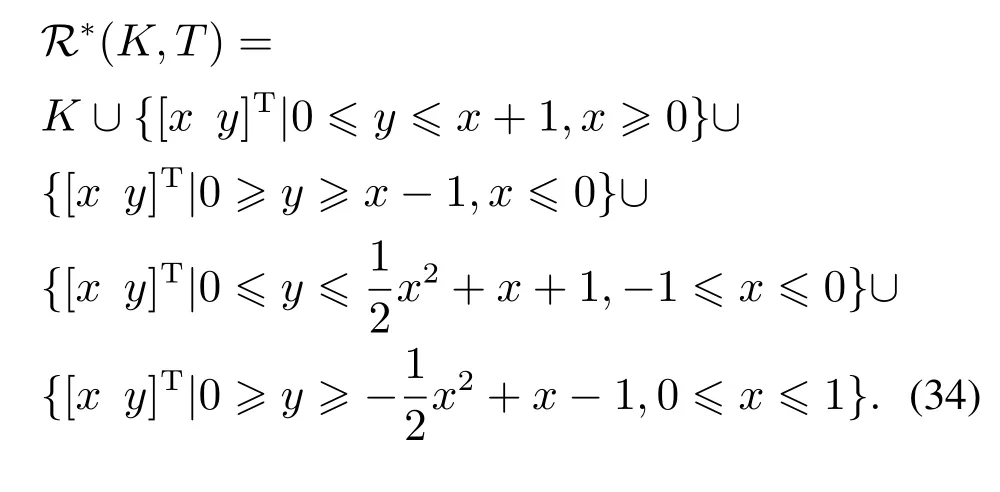
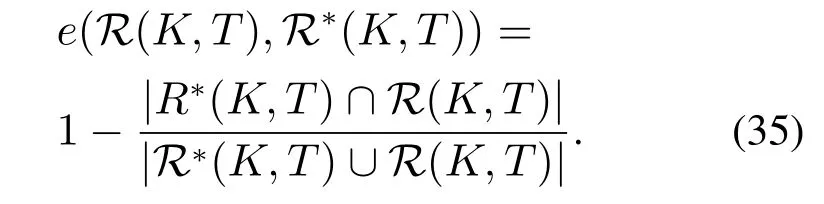
5.2 纵向飞行控制系统算例
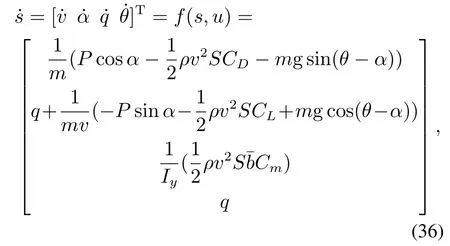
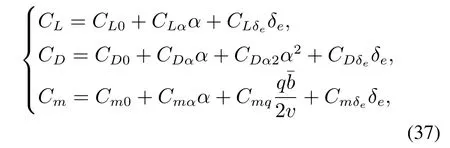
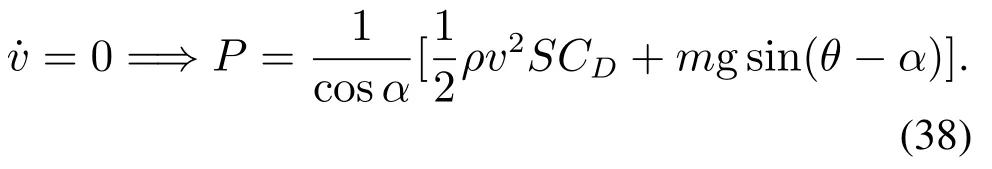
6 结论

